Giải SGK Toán 11 Chân trời sáng tạo tập 2 trang 32, 33
Giải bài 1, 2, 3, 4, 5, 6, 7 trang 32, 33 SGK Toán lớp 11 Chân trời sáng tạo tập 2. Giải các phương trình sau. Làm tròn kết quả đến hàng phần nghìn.
Bài 1 trang 32 SGK Toán 11 - Chân trời sáng tạo tập 2
Giải các phương trình sau:
a) \({5^{2x - 1}} = 25\);
b) \({3^{x + 1}} = {9^{2x + 1}}\);
c) \({10^{1 - 2x}} = 100000\).
Phương pháp:
Đưa 2 vế của phương trình về cùng cơ số.
Lời giải:
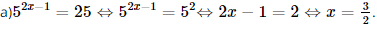
Vậy nghiệm của phương trình đã cho là x=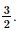
b)3x + 1 = 92x + 1 ⇔ 3x + 1 = 32(2x + 1)
⇔ x + 1 = 2(2x + 1) ⇔ x + 1 = 4x + 2
⇔ 3x = −1 ⇔ x=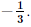
Vậy nghiệm của phương trình đã cho là x=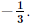
c) 101 – 2x = 100 000 ⇔ 101 – 2x = 105
⇔ 1 – 2x = 5 ⇔ 2x = – 4 ⇔ x = – 2.
Vậy nghiệm của phương trình đã cho là x = – 2.
Bài 2 trang 33 SGK Toán 11 - Chân trời sáng tạo tập 2
Giải các phương trình sau. Làm tròn kết quả đến hàng phần nghìn.
a) \({3^{x + 2}} = 7\);
b) \({3.10^{2x + 1}} = 5\).
Phương pháp:
Đưa về phương trình \({a^x} = b \Leftrightarrow x = {\log _a}b\).
Lời giải:
a) 3x + 2 = 7 ⇔ x + 3 = log3 7
⇔ x = –3 +log3 7 ⇔ x ≈ –0,229.
Vậy nghiệm của phương trình đã cho là x ≈ –0,229.
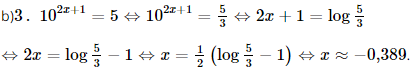
Vậy nghiệm của phương trình đã cho là x ≈ –0,389.
Bài 3 trang 33 SGK Toán 11 - Chân trời sáng tạo tập 2
Giải các phương trình sau:
a) \({\log _6}\left( {4{\rm{x}} + 4} \right) = 2\);
b) \({\log _3}x - {\log _3}\left( {x - 2} \right) = 1\).
Phương pháp:
Bước 1: Tìm ĐKXĐ.
Bước 2: Đưa 2 vế của phương trình về cùng cơ số và giải phương trình.
Bước 3: Kết luận.
Lời giải:
a) Điều kiện: 4x + 4 > 0 ⇔ x > –1
Khi đó: log6 (4x + 4) = 2 ⇔ 4x + 4 = 62
⇔ 4x + 4 = 36 ⇔ 4x = 32 ⇔ x = 8 (TMĐK)
Vậy nghiệm của phương trình đã cho là x = 8.
b) Điều kiện: 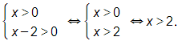
Khi đó: log3 x – log3 (x – 2) = 1
⇔ log3 x – log3 (x – 2) = 1
⇔ log3 x = log3 (x – 2) + 1
⇔ log3 x = log3 (x – 2) + log3 3
⇔ log3 x = log3 3(x – 2)
⇔ x = 3(x – 2) ⇔ 2x = 6 ⇔ x = 3 (TMĐK)
Vậy nghiệm của phương trình đã cho là x = 3.
Bài 4 trang 33 SGK Toán 11 - Chân trời sáng tạo tập 2
Giải các bất phương trình sau:
a) \({\left( {\frac{1}{3}} \right)^{2{\rm{x}} + 1}} \le 9\);
b) \({4^x} > {2^{x - 2}}\).
Phương pháp:
Đưa 2 vế của bất phương trình về cùng cơ số.
Lời giải:
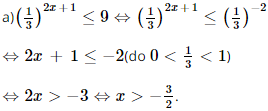
Vậy nghiệm của bất phương trình là x >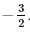
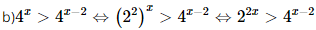
⇔ 2x > x−2 (do 2 > 1)
⇔ x > – 2.
Vậy nghiệm của bất phương trình là x > – 2.
Bài 5 trang 33 SGK Toán 11 - Chân trời sáng tạo tập 2
Giải các bất phương trình sau:
a) \({\log _2}\left( {x - 2} \right) < 2\);
b) \(\log \left( {x + 1} \right) \ge \log \left( {2x - 1} \right)\).
Phương pháp:
Bước 1: Tìm ĐKXĐ.
Bước 2: Đưa 2 vế của phương trình về cùng cơ số và giải phương trình.
Bước 3: Kết luận.
Lời giải:
a) Điều kiện: x – 2 > 0 ⇔ x > 2
Khi đó: log2 (x – 2) < 2⇔ x – 2 < 22
⇔ x – 2 < 4 ⇔ x < 6.
Kết hợp với điều kiện ta được nghiệm của bất phương trình là 2 < x < 6.
b) Điều kiện:
Khi đó: log (x + 1) ≥ log (2x – 1)
⇔ x + 1 ≥ 2x – 1 ⇔ x ≥ –2 ⇔ x ≤ 2.
Kết hợp với điều kiện ta được nghiệm của bất phương trình là 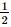 < x ≤ 2
< x ≤ 2
Bài 6 trang 33 SGK Toán 11 - Chân trời sáng tạo tập 2
Chất phóng xạ polonium-210 có chu kì bán rã là 138 ngày. Điều này có nghĩa là cứ sau 138 ngày, lượng polonium còn lại trong một mẫu chỉ bằng một nửa lượng ban đầu. Một mẫu 100 g có khối lượng polonium-210 còn lại sau \(t\) ngày được tính theo công thức \(M\left( t \right) = 100{\left( {\frac{1}{2}} \right)^{\frac{t}{{138}}}}\)(g).
(Nguồn:https://pubchem.ncbi.nlm.nih.gov/element/Polonium#section=Atomic-Mass-Half-Life-and-Decay)
a) Khối lượng polonium-210 còn lại bao nhiêu sau 2 năm?
b) Sau bao lâu thì còn lại 40 g polonium-210?
Phương pháp:
a) Tìm \(t\), sau đó thay vào công thức \(M\left( t \right) = 100{\left( {\frac{1}{2}} \right)^{\frac{t}{{138}}}}\).
b) Thay \(M\left( t \right) = 40\) vào công thức \(M\left( t \right) = 100{\left( {\frac{1}{2}} \right)^{\frac{t}{{138}}}}\).
Lời giải:
a) Sau 2 năm (tức t = 730), khối lượng polonium-210 còn lại là:
M(730)=100=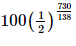 ≈1,92 (g)
≈1,92 (g)
Vậy khối lượng polonium-210 còn lại sau 2 năm khoảng 1,92 g.
b) Ta có 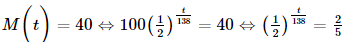
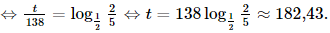
Vậy sau khoảng 182,43 ngày thì còn lại 40 g polonium-210.
Bài 7 trang 33 SGK Toán 11 - Chân trời sáng tạo tập 2
Nhắc lại rằng, mức cường độ âm \(L\) được tính bằng công thức \(L = 10\log \left( {\frac{I}{{{I_0}}}} \right)\left( {dB} \right)\), trong đó \(I\) là cường độ của âm tính bằng \(W/{m^2}\) và \({I_0} = {10^{ - 12}}W/{m^2}\).
(Nguồn: Vật lí 12, NXB Giáo dục Việt Nam, năm 2017, trang 52)
a) Một giáo viên đang giảng bài trong lớp học có mức cường độ âm là 50 dB. Cường độ âm của giọng nói giáo viên bằng bao nhiêu?
b) Mức cường độ âm trong một nhà xưởng thay đổi trong khoảng từ 75 dB đến 90 dB. Cường độ âm trong nhà xưởng này thay đổi trong khoảng nào?
Phương pháp:
a) Thay \(L = 50\) và giải phương trình.
b) Giải bất phương trình \(75 \le L \le 90\).
Lời giải:
a) Ta có L=50⇔10log 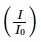 =50⇔10log
=50⇔10log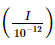 =50
=50
⇔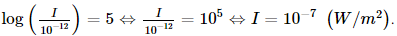
b) Ta có 75≤L≤90 ⇔ 75≤10log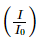 ≤90
≤90
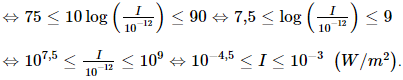
Vậy cường độ âm trong nhà xưởng này thay đổi trong khoảng 10–4,5 (W/m2) đến 10–3 (W/m2).
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài tập cuối chương 9
- Bài 2. Biến cố hợp và quy tắc cộng xác suất
- Bài 1. Biến cố giao và quy tắc nhân xác suất
- CHƯƠNG IX. XÁC SUẤT
- Bài tập cuối chương 8
- Bài 5. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
- Bài 4. Khoảng cách trong không gian
- Bài 3. Hai mặt phẳng vuông góc
- Bài 2. Đường thẳng vuông góc với mặt phẳng
- Bài 1. Hai đường thẳng vuông góc
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
