Giải SGK Toán 11 Chân trời sáng tạo tập 2 trang 81, 82
Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 81,82 SGK Toán lớp 11 Chân trời sáng tạo tập 2. Tính thể tích của khối chóp cụt lục giác đều (ABCDEF.{rm{ }}A'B'C'D'E'F') với (O) và (O') là tâm hai đáy, cạnh đáy lớn và đáy nhỏ lần lượt là (a) và (frac{a}{2},OO' = a).
Bài 1 trang 81 SGK Toán 11 - Chân trời sáng tạo tập 2
Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình thoi cạnh \(a\) có \(O\) là giao điểm của hai đường chéo, \(\widehat {ABC} = {60^ \circ },SO \bot \left( {ABCD} \right),SO = a\sqrt 3 \). Tính khoảng cách từ \(O\) đến mặt phẳng \(\left( {SCD} \right)\).
Phương pháp:
Cách tính khoảng cách từ một điểm đến một mặt phẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên mặt phẳng.
Lời giải:
Kẻ OI ⊥ CD, OH ⊥ SI
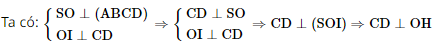
Mà OH ⊥ SI Suy ra OH ⊥ (SCD)
Do đó d(O, (SCD)) = OH.
Ta có: ΔABC đều ⇒ OC = 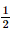 AC =
AC = 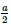
• Xét ΔABD, áp dụng định lí cos, ta có:
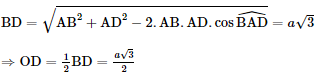
• Xét ΔOCD vuông tại O có OI là đường cao:
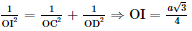
Ta có SO ⊥ (ABCD) ⇒ SO ⊥ OI
Do đó, tam giác SOI vuông tại O có OH là đường cao nên
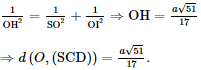
Vậy khoảng cách từ O đến mặt phẳng (SCD) là 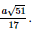
Bài 2 trang 81 SGK Toán 11 - Chân trời sáng tạo tập 2
Cho hai tam giác cân \(ABC\) và \(ABD\) có đáy chung \(AB\) và không cùng nằm trong một mặt phẳng.
a) Chứng minh rằng \(AB \bot CD\).
b) Xác định đoạn vuông góc chung của \(AB\) và \(C{\rm{D}}\).
Phương pháp:
‒ Cách chứng minh hai đường thẳng vuông góc:
Cách 1: Chứng minh góc giữa chúng bằng \({90^ \circ }\).
Cách 2: Chứng minh đường thẳng này vuông góc với một mặt phẳng chứa đường thẳng kia.
‒ Cách dựng đoạn vuông góc chung của hai đường thẳng \(a\) và \(b\) vuông góc với nhau:
Bước 1: Xác định mặt phẳng \(\left( P \right)\) chứa \(b\) mà \(\left( P \right)\) vuông góc với \(a\).
Bước 2: Tìm giao điểm \(I = \left( P \right) \cap a\).
Bước 3: Kẻ \(IA \bot b\left( {A \in b} \right)\), chứng minh \(IA \bot a\). Khi đó \(d\left( {a,b} \right) = IA\).
Lời giải:
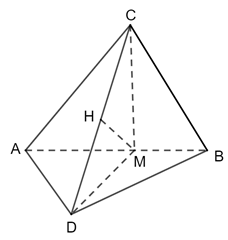
a) Gọi M là trung điểm của AB.
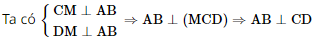
b) Gọi H là hình chiếu vuông góc M của trên CD.
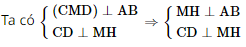
Do đó MH là đoạn vuông góc chung của AB và CD.
Bài 3 trang 81 SGK Toán 11 - Chân trời sáng tạo tập 2
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), \(SA = SB = SC = SD = a\sqrt 2 \). Gọi \(I,J\) lần lượt là trung điểm của \(AB\) và \(C{\rm{D}}\).
a) Chứng minh \(AB \bot \left( {SIJ} \right)\).
b) Tính khoảng cách giữa hai đường thẳng \(AB\) và \(SC\).
Phương pháp:
‒ Cách chứng minh đường thẳng vuông góc với mặt phẳng: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.
‒ Cách tính khoảng cách giữa hai đường thẳng chéo nhau:
Cách 1: Dựng đường vuông góc chung.
Cách 2: Tính khoảng cách từ đường thẳng này đến một mặt phẳng song song với đường thẳng đó và chứa đường thẳng còn lại.
Lời giải:
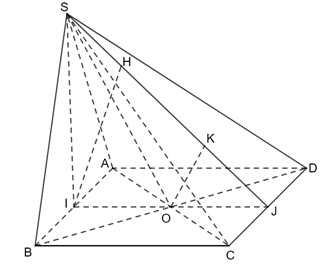
a) Ta có: ΔSAB cân tại S và đáy là hình vuông ABCD.
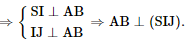
b) Ta có: AB // CD ⇒ AB // (ABCD)
⇒ d(AB, SC) = d(AB, (SCD)) = d(I, (SCD))
Gọi H, K lần lượt là hình chiếu vuông góc của I, O trên SJ
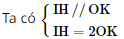
Vì AB // CD nên CD ⊥ (SIJ) ⇒ CD ⊥ IH ⇒IH ⊥ (SCD)
⇒ d(AB, CD) = d(AB, (SCD)) = IH = 2OK
Ta có: ABCD là hình vuông
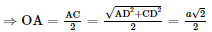
• Xét ΔSAO vuông tại O có
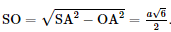
• Xét ΔSOJ vuông tại O có đường cao OK nên
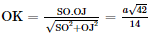
Do đó dAB,SC= 2OK = 
Bài 4 trang 81 SGK Toán 11 - Chân trời sáng tạo tập 2
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có \(AB = a\), góc giữa hai mặt phẳng \(\left( {A'BC} \right)\) và \(\left( {ABC} \right)\) bằng \({60^ \circ }\).
a) Tính khoảng cách giữa hai đáy của hình lăng trụ.
b) Tinh thể tích của khối lăng trụ.
Phương pháp:
‒ Cách tính khoảng cách giữa hai mặt phẳng song song: Tính khoảng cách một điểm nằm trên mặt phẳng này đến mặt phẳng còn lại.
‒ Công thức tính thể tích khối lăng trụ: \(V = Sh\).
Lời giải:
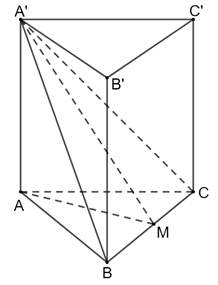
a) Vì khối lăng trụ đều nên gọi là trung điểm của BC AM ⊥ BC. Do đó góc giữa hai mặt phẳng ((A′BC), (ABC)) 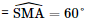
Do đó khoảng cách giữa hai đáy của lăng trụ là:
 .
.
b) Thể tích khối lăng trụ là: 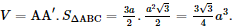
Bài 5 trang 81 SGK Toán 11 - Chân trời sáng tạo tập 2
Một cây cầu dành cho người đi bộ (Hình 22) có mặt sàn cầu cách mặt đường 3,5 m, khoảng cách từ đường thẳng \(a\) nằm trên tay vịn của cầu đến mặt sàn cầu là 0,8 m. Gọi \(b\) là đường thẳng kẻ theo tim đường. Tính khoảng cách giữa hai đường thẳng \(a\) và \(b\).

Phương pháp:
Cách tính khoảng cách giữa hai đường thẳng chéo nhau:
Cách 1: Dựng đường vuông góc chung.
Cách 2: Tính khoảng cách từ đường thẳng này đến một mặt phẳng song song với đường thẳng đó và chứa đường thẳng còn lại.
Lời giải:
Vì tay vịn cầu song song với mặt đường nên khoảng cách giữa hai đường thẳng a và b
chính bằng khoảng cách từ đường thẳng a xuống mặt đường.
Khoảng cách giữa hai đường thẳng a và b bằng: 3,5 + 0,8 = 4,3(m).
Vậy khoảng cách giữa hai đường thẳng a và b là 4,3 m.
Bài 6 trang 82 SGK Toán 11 - Chân trời sáng tạo tập 2
Cho hình hộp đứng \(ABCD.A'B'C'D'\) có cạnh bên \(AA' = 2a\) và đáy \(ABCD\) là hình thoi có \(AB = a\) và \(AC = a\sqrt 3 \).
a) Tính khoảng cách giữa hai đường thẳng \(B{\rm{D}}\) và \(AA'\).
b) Tính thể tích của khối hộp.
Phương pháp:
‒ Cách tính khoảng cách giữa hai đường thẳng chéo nhau:
Cách 1: Dựng đường vuông góc chung.
Cách 2: Tính khoảng cách từ đường thẳng này đến một mặt phẳng song song với đường thẳng đó và chứa đường thẳng còn lại.
‒ Công thức tính thể tích khối lăng trụ: \(V = Sh\).
Lời giải:
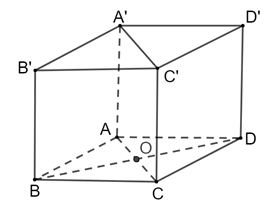
a) Vì hình hộp đứng ABCD.A'B'C'D'">ABCD.A′B′C′D′ABCDN có đáy ABCD là hình thoi tâm O.
Do đó ta có: 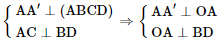
Suy ra là đoạn vuông góc chung của hai đường thẳng BD và AA'.
Do đó 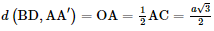
b) Đáy ABCD là hình thoi tâm O có AB = a và 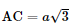
BD = 2OB = 
Thể tích của khối hộp là: 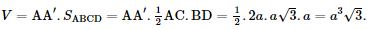
Vậy thể tích của khối hộp là 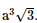
Bài 7 trang 82 SGK Toán 11 - Chân trời sáng tạo tập 2
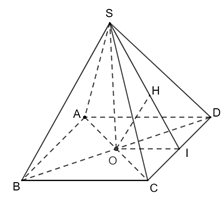
Cho hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh đều bằng \(a\) và có \(O\) là giao điểm hai đường chéo của đáy.
a) Tính khoảng cách giữa hai đường thẳng \(AC\) và \(SB\).
b) Tinh thể tích của khối chóp.
Phương pháp:
‒ Cách tính khoảng cách giữa hai đường thẳng chéo nhau:
Cách 1: Dựng đường vuông góc chung.
Cách 2: Tính khoảng cách từ đường thẳng này đến một mặt phẳng song song với đường thẳng đó và chứa đường thẳng còn lại.
‒ Công thức tính thể tích khối chóp: \(V = \frac{1}{3}Sh\).
Lời giải:
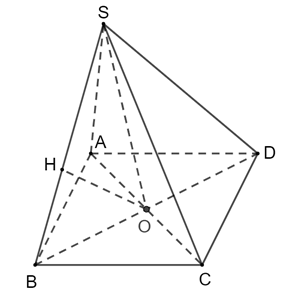
a) Kẻ OH ⊥ SB (H ∈">∈∈SB)
S.ABCD là hình chóp tứ giác đều ⇒ SO ⊥ (ABCD) ⇒ SO ⊥AC.
Tứ giác ABCD là hình vuông suy ra AC ⊥ BD ⇒ AC ⊥(SBD) ⇒AC ⊥ OH.
Mà OH ⊥ SB
Do đó d(AC, SB) = OH
• Xét ΔABD vuông tại A, ta có:
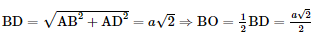
• Xét ΔSBO vuông tại O, ta có:
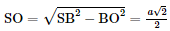
• Xét ΔSBO vuông tại O có SO = BO nên ΔSBO vuông cân tại O
Suy ra OH vừa là đường cao, vừa là đường trung tuyến.
Do đó 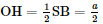
Vậy d(AC,SB)=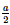
b) 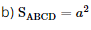 .
.
Thể tích khối chóp là 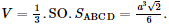
Bài 8 trang 82 SGK Toán 11 - Chân trời sáng tạo tập 2
Tính thể tích của khối chóp cụt lục giác đều \(ABCDEF.{\rm{ }}A'B'C'D'E'F'\) với \(O\) và \(O'\) là tâm hai đáy, cạnh đáy lớn và đáy nhỏ lần lượt là \(a\) và \(\frac{a}{2},OO' = a\).
Phương pháp:
Sử dụng công thức tính thể tích khối chóp cụt đều: \(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right)\).
Lời giải:
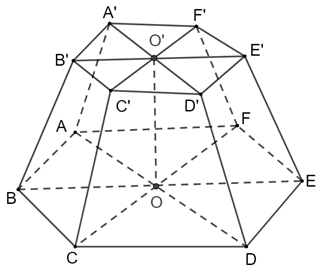
Ta có mỗi hình lục giác đều được tạo bởi 6 tam giác đều có cạnh bằng cạnh của hình lục giác.
Do đó ta có diện tích các đáy là: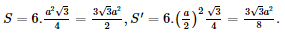
Chiều cao của khối chóp cụt là: h = OO′ = a
Thể tích khối chóp cụt là: 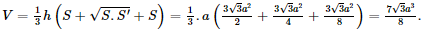
Vậy thể tích khối chóp cụt là 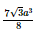
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài tập cuối chương 9
- Bài 2. Biến cố hợp và quy tắc cộng xác suất
- Bài 1. Biến cố giao và quy tắc nhân xác suất
- CHƯƠNG IX. XÁC SUẤT
- Bài tập cuối chương 8
- Bài 5. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
- Bài 4. Khoảng cách trong không gian
- Bài 3. Hai mặt phẳng vuông góc
- Bài 2. Đường thẳng vuông góc với mặt phẳng
- Bài 1. Hai đường thẳng vuông góc
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
