Giải SGK Toán 11 trang 19, 20 Chân trời sáng tạo tập 1
Giải bài 1, 2, 3, 4, 5, 6 trang 19, bài 7, 8 trang 20 SGK Toán lớp 11 Chân trời sáng tạo tập 1. Các đẳng thức sau có thể đồng thời xảy ra không?
Bài 1 trang 19 SGK Toán 11 tập 1 - Chân trời sáng tạo
Các đẳng thức sau có thể đồng thời xảy ra không?
a) \(\sin \alpha = \frac{3}{5}\) và \(\cos \alpha = - \frac{4}{5}\)
b) \(\sin \alpha = \frac{1}{3}\) và \(\cot \alpha = \frac{1}{2}\)
c) \(\tan \alpha = 3\) và \(\cot \alpha = \frac{1}{3}\)
Phương pháp:
Dựa vào công thức đã học để xác định
Lời giải:
a) Ta có: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Leftrightarrow {\left( {\frac{3}{5}} \right)^2} + {\cos ^2}\alpha = 1 \Leftrightarrow \cos \alpha = \pm \frac{4}{5}\)
Đẳng thức có thể đồng thời xảy ra
b) Ta có: \(1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }} \Rightarrow 1 + {\cot ^2}\alpha = \frac{1}{{{{\left( {\frac{1}{3}} \right)}^2}}} \Rightarrow \cot \alpha = \pm 2\sqrt 2 \)
Hai đẳng thức không thể đồng thời xảy ra
c) Ta có: \(\tan \alpha .\cot \alpha = 1 \Rightarrow 3.\cot \alpha = 1 \Rightarrow \cot \alpha = \frac{1}{3}\)
Đẳng thức có thể đồng thời xảy ra
Bài 2 trang 19 SGK Toán 11 tập 1 - Chân trời sáng tạo
Cho \(\sin \alpha = \frac{{12}}{{13}}\) và \(\cos \alpha = - \frac{5}{{13}}\). Tính \(\sin \left( { - \frac{{15\pi }}{2} - \alpha } \right) - \cos \left( {13\pi + \alpha } \right)\)
Phương pháp:
Dựa vào công thức lượng giác đặc biệt để tính
\(\cos \left( { \pi + \alpha } \right) = - \cos \left( \alpha \right)\)
\(\sin \left( {\frac{\pi }{2} - \alpha } \right) = \cos \left( \alpha \right)\)
\(\begin{array}{l}\sin (\alpha + k2\pi ) = \sin \alpha ;\,\\\cos (\alpha + k2\pi ) = \cos \alpha \end{array}\)
Lời giải:
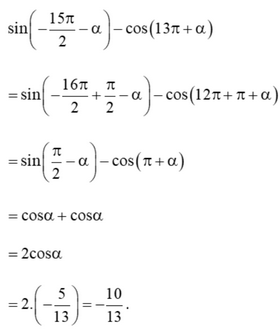
Bài 3 trang 19 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tính các giá trị lượng giác của góc α, nếu:
a) \(\sin \alpha = \frac{5}{{13}}\) và \(\frac{\pi }{2} < \alpha < \pi \)
b) \(\cos \alpha = \frac{2}{5}\) và \(0 < \alpha < 90^\circ \)
c) \(\tan \alpha = \sqrt 3 \) và \(\pi < \alpha < \frac{{3\pi }}{2}\)
d) \(\cot \alpha = \frac{1}{2}\) và \(270^\circ < \alpha < 360^\circ \)
Phương pháp:
Dựa vào hệ thức cơ bản của hàm lượng giác để tính
Lời giải:
a) Ta có: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Rightarrow {\left( {\frac{5}{{13}}} \right)^2} + {\cos ^2}\alpha = 1 \Rightarrow \cos \alpha = \pm \frac{{12}}{{13}}\)
Do \(\frac{\pi }{2} < \alpha < \pi \Rightarrow \cos \alpha = \frac{-{12}}{{13}}\)\( \Rightarrow \left\{ \begin{array}{l}\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{-5}{{12}}\\\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{-{12}}{5}\end{array} \right.\)
b) Ta có: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Rightarrow {\left( {\frac{2}{5}} \right)^2} + {\sin ^2}\alpha = 1 \Rightarrow \sin \alpha = \pm \frac{{\sqrt {21} }}{5}\)
Do \(0 < \alpha < 90^\circ \Rightarrow \sin \alpha = \frac{{\sqrt {21} }}{5}\)\( \Rightarrow \left\{ \begin{array}{l}\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{\sqrt {21} }}{2}\\\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{2\sqrt {21} }}{{21}}\end{array} \right.\)
c) Ta có: \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }} \Rightarrow 1 + {\left( {\sqrt 3 } \right)^2} = \frac{1}{{{{\cos }^2}\alpha }} \Rightarrow \cos \alpha = \pm \frac{1}{2}\)
Do \(\pi < \alpha < \frac{{3\pi }}{2} \Rightarrow \cos \alpha = \frac{-1}{2}\) \( \Rightarrow \left\{ \begin{array}{l}\cot \alpha .\tan \alpha = 1\\\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\cot \alpha = \frac{{\sqrt 3 }}{3}\\\sin \alpha = \frac{{-\sqrt 3 }}{2}\end{array} \right.\)
d) Ta có: \(1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }} \Rightarrow 1 + {\left( {\frac{1}{2}} \right)^2} = \frac{1}{{{{\sin }^2}\alpha }} \Rightarrow \sin \alpha = \pm \frac{{2\sqrt 5 }}{5}\)
Do \(270^\circ < \alpha < 360^\circ \Rightarrow \sin \alpha = \frac{{-2\sqrt 5 }}{5}.\)
Ta có: \(\cot \alpha = \frac{1}{2} \Rightarrow \tan \alpha = \frac{1}{{\cot \alpha }} = 2\)
Lại có:
\(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }} \Leftrightarrow 1 + 4 = \frac{1}{{{{\cos }^2}\alpha }}\)\( \Leftrightarrow {\cos ^2}\alpha = \frac{1}{5} \Leftrightarrow \cos \alpha = \pm \frac{{\sqrt 5 }}{5}\)
Do \({270^o} < \alpha < {360^o} \Rightarrow \cos \alpha > 0 \Rightarrow \cos \alpha = \frac{{\sqrt 5 }}{5}\)
Bài 4 trang 19 SGK Toán 11 tập 1 - Chân trời sáng tạo
Biểu diễn các giá trị lượng giác sau qua giá trị lượng giác của góc có số đo từ 0 đến \(\frac{\pi }{4}\) hoặc từ 0 đến \(45^\circ \) và tính
a) \(\cos \frac{{21\pi }}{6}\)
b) \(\sin \frac{{129\pi }}{4}\)
c) \(\tan 1020^\circ \)
Phương pháp:
Dựa vào kiến thức vừa học được để tách các góc lượng giác
Lời giải:
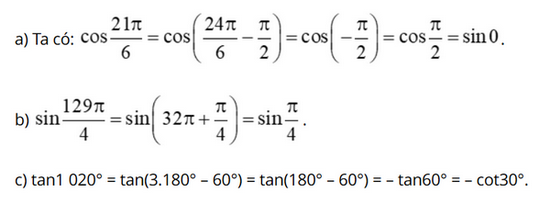
Bài 5 trang 19 SGK Toán 11 tập 1 - Chân trời sáng tạo
Chứng minh các đẳng thức lượng giác sau:
a) \({\sin ^4}\alpha - {\cos ^4}\alpha = 1 - 2{\cos ^2}\alpha \)
b) \(\tan \alpha + \cot \alpha = \frac{1}{{\sin \alpha .\cos \alpha }}\)
Phương pháp:
Dựa vào các hệ thức cơ bản của lượng giác để chứng minh
Lời giải:
a) Ta có:
\(\begin{array}{l}{\sin ^4}\alpha - {\cos ^4}\alpha = 1 - 2{\cos ^2}\alpha \\ \Leftrightarrow \left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right)\left( {{{\sin }^2}\alpha - {{\cos }^2}\alpha } \right) = 1 - 2{\cos ^2}\alpha \\ \Leftrightarrow {\sin ^2}\alpha - {\cos ^2}\alpha - 1 + 2{\cos ^2}\alpha = 0\\ \Leftrightarrow {\sin ^2}\alpha + {\cos ^2}\alpha - 1 = 0\\ \Leftrightarrow 1 - 1 = 0\\ \Leftrightarrow 0 = 0\end{array}\)
Đẳng thức luôn đúng
b) Ta có:
\(\begin{array}{l}\tan \alpha + \cot \alpha = \frac{1}{{\sin \alpha .\cos \alpha }}\\ \Leftrightarrow \frac{{\sin \alpha }}{{\cos \alpha }} + \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{1}{{\sin \alpha .\cos \alpha }}\\ \Leftrightarrow \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{\cos \alpha .\sin \alpha }} = \frac{1}{{\sin \alpha .\cos \alpha }}\\ \Leftrightarrow \frac{1}{{\sin \alpha .\cos \alpha }} = \frac{1}{{\sin \alpha .\cos \alpha }}\end{array}\)
Đẳng thức luôn đúng
Bài 6 trang 19 SGK Toán 11 tập 1 - Chân trời sáng tạo
Rút gọn các biểu thức sau:
a) \(\frac{1}{{\tan \alpha + 1}} + \frac{1}{{\cot \alpha + 1}}\)
b) \(\cos \left( {\frac{\pi }{2} - \alpha } \right) - \sin \left( {\pi + \alpha } \right)\)
c) \(\sin \left( {\alpha - \frac{\pi }{2}} \right) + \cos \left( { - \alpha + 6\pi } \right) - \tan \left( {\alpha + \pi } \right)\cot \left( {3\pi - \alpha } \right)\)
Phương pháp:
Kết hợp giữa công thức cơ bản của lượng giác và hệ thức lượng giác để rút gọn
Lời giải:
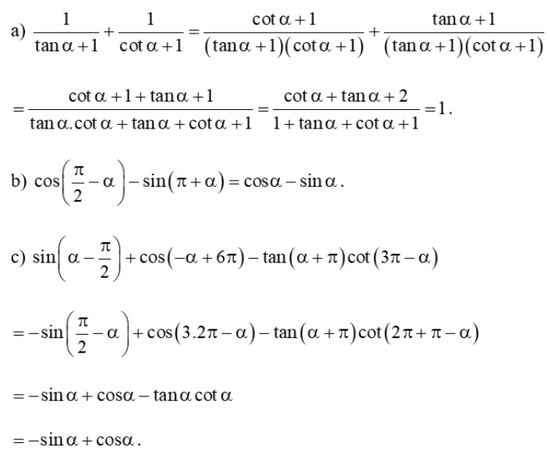
Bài 7 trang 20 SGK Toán 11 tập 1 - Chân trời sáng tạo
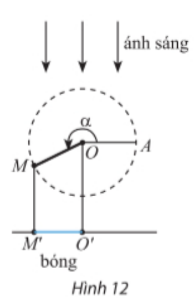
Thanh OM quay ngược chiều kim đồng hồ quanh trục O của nó trên một mặt phẳng thẳng đứng và in bóng vuông góc xuống mặt đất như Hình 12. Vị trí ban đầu của thanh là OA. Hỏi độ dài bóng O’M’ của OM khi thanh quay được \(3\frac{1}{{10}}\) vòng là bao nhiêu, biết thanh độ dài OM là 15cm? Kết quả làm trong đến hàng phần mười.
Phương pháp:
Dựa vào hàm lượng giác cơ bản để tính
Lời giải:
Thanh OM quay được \(3\frac{1}{{10}}\) \( \Rightarrow \alpha = 3\frac{1}{{10}}.360^\circ = 1116^\circ \)
Kẻ MH vuông góc Ox
Khi đó \(\begin{array}{l}M\left( {15.\cos 1116^\circ ;15.\sin 1116^\circ } \right)\\ \Rightarrow OH = \left| {\cos 1116^\circ } \right|.15 \approx 12,1\end{array}\)
Vậy độ dài bóng O’M’ của OM khi thanh quay được \(3\frac{1}{{10}}\) là 12,1cm
Bài 8 trang 20 SGK Toán 11 tập 1 - Chân trời sáng tạo
Khi xe đạp di chuyển, van V của bánh xe quay quanh trục O theo chiều kim đồng hồ với tốc độ góc không đổi là 11 rad/s (Hình 13). Ban đầu van nằm ở vị trí A. Hỏi sau một phút di chuyển, khoảng cách từ van đến mặt đất là bao nhiêu, biết bán kính OA = 58cm? Giả sử độ dày của lốp xe không đáng kể. Kết quả làm trong đến hàng phần mười.

Phương pháp:
Dựa vào kiến thức đã học để làm
Lời giải:
Sau một phút di chuyển, van V đã quay được một góc lượng giác có số đo góc là: α = 11.60 = 660 (rad).
Khi đó tọa độ điểm V biểu diễn cho góc lượng giác trên có tọa độ là:
Khi đó khoảng cách từ van đến mặt đất khoảng 58 – 15,2 = 42,8 cm.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài tập cuối chương 9
- Bài 2. Biến cố hợp và quy tắc cộng xác suất
- Bài 1. Biến cố giao và quy tắc nhân xác suất
- CHƯƠNG IX. XÁC SUẤT
- Bài tập cuối chương 8
- Bài 5. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
- Bài 4. Khoảng cách trong không gian
- Bài 3. Hai mặt phẳng vuông góc
- Bài 2. Đường thẳng vuông góc với mặt phẳng
- Bài 1. Hai đường thẳng vuông góc
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
