Giải SGK Toán 12 tập 1 Chân trời sáng tạo trang 18

Bài 1 trang 18 SGK Toán 12 Tập 1 Chân trời sáng tạo

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đồ thị được cho ở Hình 5

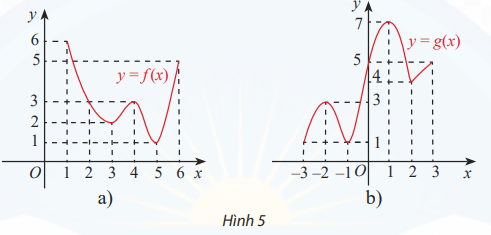
Phương pháp:

Quan sát đồ thị, xác định giá trị lớn nhất và giá trị nhỏ nhất bằng cách:

- Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên D nếu f(x) \( \le \) M với mọi x thuộc D và tồn tại \({x_0}\) thuộc D sao cho f(\({x_0}\)) = M. Kí hiệu M = \(\mathop {\max }\limits_D \)f(x). Số m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên D nếu f(x) \( \ge \) m với mọi x thuộc D và tồn tại \({x_0}\) thuộc D sao cho f(\({x_0}\)) = m. Kí hiệu m = \(\mathop {\min }\limits_D \)f(x).

Lời giải:

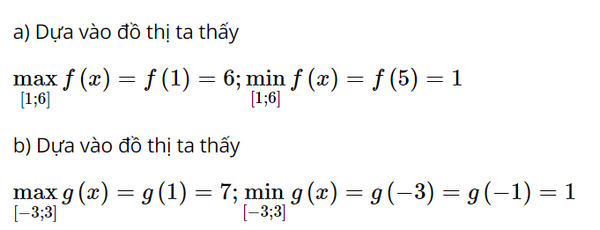
Bài 2 trang 18 SGK Toán 12 Tập 1 Chân trời sáng tạo

Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) \(y = {x^3} - 12x + 1\) trên đoạn [-1;3]
b) \(y = - {x^3} + 24{x^2} - 180x + 400\) trên đoạn [3;11]
c) \(y = \frac{{2x + 1}}{{x - 2}}\) trên đoạn [3;7]
d) \(y = \sin 2x\) trên đoạn \([0;\frac{{7\pi }}{{12}}]\)

Phương pháp:

Tìm đạo hàm, lập bảng biến thiên và xác định giá trị lớn nhất, giá trị nhỏ nhất của hàm số

Lời giải:

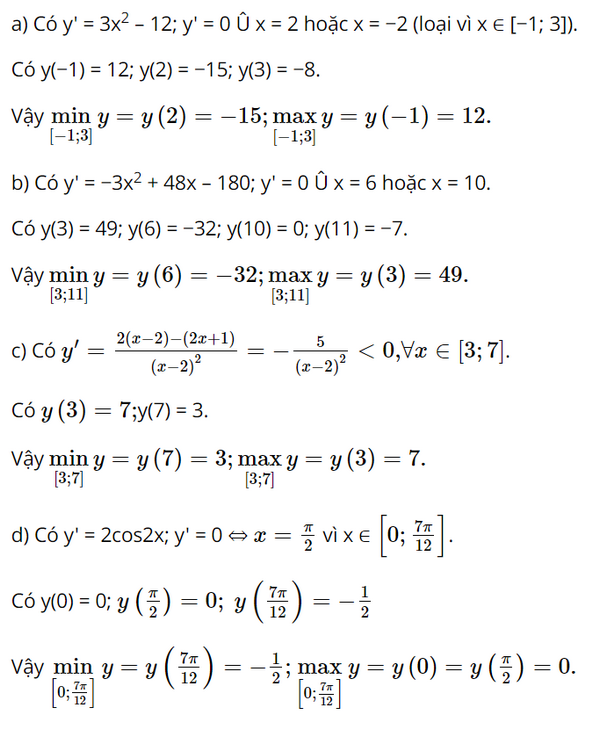
Bài 3 trang 18 SGK Toán 12 Tập 1 Chân trời sáng tạo

Tìm giá trị nhỏ nhất của các hàm số sau:
a) \(y = {x^3} - 3x - 4\) trên nửa khoảng [-3;2)
b) \(y = \frac{{3{x^2} - 4x}}{{{x^2} - 1}}\) trên khoảng \(( - 1; + \infty )\)

Phương pháp:

Tìm đạo hàm, lập bảng biến thiên và xác định giá trị nhỏ nhất

Lời giải:

a) Có y' = 3x² – 3; y' = 0 ⇔ x = −1 hoặc x = 1.

Bảng biến thiên

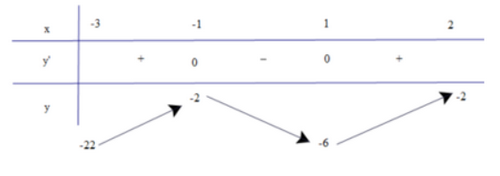
Dựa vào bảng biến thiên ta có:

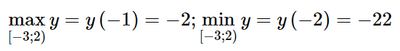
b) Trên khoảng (−1; +∞) hàm số không xác định tại x = 1.

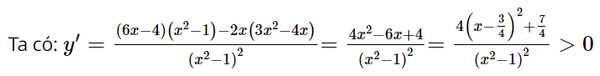
Bảng biến thiên

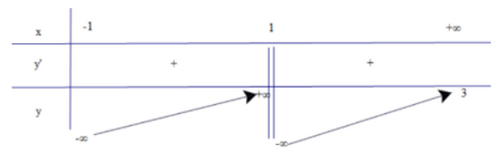
Hàm số không có giá trị nhỏ nhất trên khoảng (−1; +∞).

Bài 4 trang 18 SGK Toán 12 Tập 1 Chân trời sáng tạo

Khi làm nhà kho, bác An muốn cửa sổ có dạng hình chữ nhật với chu vi bằng 4m (Hình 6). Tìm kích thước khung cửa sổ sao cho diện tích cửa sổ lớn nhất (để hứng được nhiều ánh sáng nhất)?

Phương pháp:

Tìm mối liên hệ giữa chiều dài và chiều rộng của cửa, sau đó lập hàm số của diện tích cửa sổ, tìm đạo hàm, vẽ bảng biến thiên và xác định giá trị lớn nhất của diện tích

Lời giải:

Nửa chu vi khung cửa số là 4 : 2 = 2 (m).

Gọi chiều dài khung cửa sổ là x (m) (0 < x < 2).

Chiều rộng khung cửa sổ là 2 – x (m).

Diện tích khung cửa số là S(x) = x(2 – x) = 2x – x² (m²).

Bài toán trở thành tìm giá trị lớn nhất của hàm số S(x).

Ta có S'(x) = 2 – 2x; S'(x) = 0 ⇔ x = 1.

Bảng biến thiên

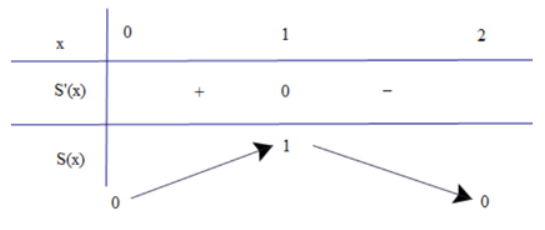
Diện tích của cửa sổ lớn nhất là 1 m² khi đó khung cửa số có dạng hình vuông cạnh 1m.

Bài 5 trang 18 SGK Toán 12 Tập 1 Chân trời sáng tạo

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = 2\sqrt {1 - {x^2}}  + {x^2}\)

Phương pháp:

tìm tập xác định, tìm đạo hàm, lập bảng biến thiên và xác định giá trị lớn nhất, giá trị nhỏ nhất

Lời giải:

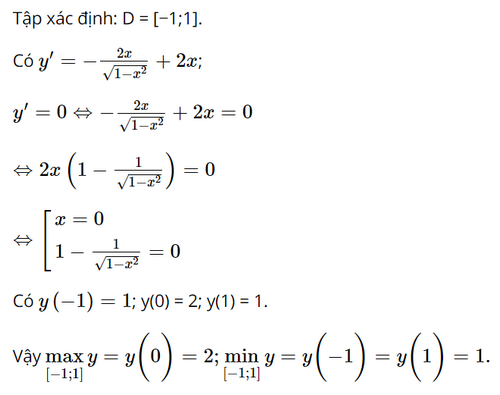
Bài 6 trang 18 SGK Toán 12 Tập 1 Chân trời sáng tạo

Khối lượng \(q\) (kg) của một mặt hàng mà cửa tiệm bán được trong một ngày phụ thuộc vào giá bán \(p\) (nghìn đồng/kg) theo công thức \(p = 15 - \frac{1}{2}q\). Doanh thu từ việc bán mặt hàng trên của cửa tiệm được tính theo công thức \(R = pq\).

a) Viết công thức biểu diễn \(R\) theo \(p\).

b) Tìm giá bán mỗi kilôgam sản phẩm để đạt được doanh thu cao nhất và xác định doanh thu cao nhất đó.

Phương pháp:

a) Biến đổi công thức \(p = 15 - \frac{1}{2}q\) để tìm biểu thức biểu diễn \(q\) theo \(p\), sau đó thay vào công thức \(R = pq\)

b) Lập hàm số từ công thức trên biểu diễn theo \(p\), tìm đạo hàm, lập bảng biến thiên và xác định giá trị lớn nhất

Lời giải:

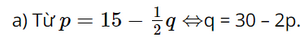
Khi đó R = pq = p(30 – 2p) = −2p² + 30p.

b) Bài toán trở thành tìm giá trị lớn nhất của hàm số R = −2p² + 30p với p > 0.

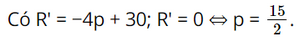
Bảng biến thiên

Vậy bán mỗi sản phẩm giá 7,5 nghìn đồng thì đạt doanh thu cao nhất là 112,5 nghìn đồng.

Bài 7 trang 18 SGK Toán 12 Tập 1 Chân trời sáng tạo

Hộp sữa \(1l\) được thiết kế dạng hình hộp chữ nhật với đáy là hình vuông cạnh x cm. Tìm x để diện tích toàn phần của hộp nhỏ nhất.

Phương pháp:

Tìm mối liên hệ giữa chiều cao và cạnh đáy, từ đó lập hàm số biểu diễn diện tích toàn phần của hộp theo x. Sau đó tìm đạo hàm, lập bảng biến thiên và xác định giá trị nhỏ nhất

Lời giải:

Gọi chiều cao của hộp sữa là h (cm), h > 0.

Theo đề ta có V = 1 lít = 1000 cm³ = x².h ⇔h=1000x2⇔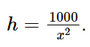

Diện tích toàn phần của hộp sữa là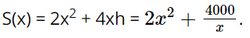 

Bài toán trở thành tìm giá trị nhỏ nhất của hàm số S(x) khi x > 0.

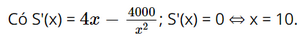
Bảng biến thiên

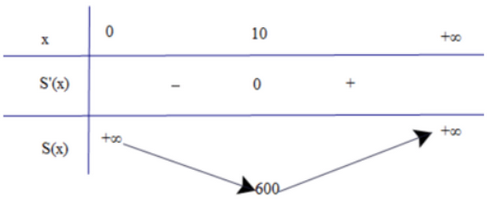
Vậy diện tích toàn phần của hộp nhỏ nhất khi x = 10 cm.

Sachbaitap.com