Giải SGK Toán 12 tập 1 Chân trời sáng tạo trang 82, 83

Bài 1 trang 82 SGK Toán 12 Tập 1 Chân trời sáng tạo

Bảng dưới đây thống kê cự li ném tạ của một vận động viên.

Hãy tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm trên.

Phương pháp:

Tính giá trị đại diện

Phương sai của mẫu số liệu ghép nhóm, kí hiệu \({S^2}\), được tính bởi công thức:

\({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}]\)

Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu

\(\overline x  = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k})\) là số trung bình

Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu \(S\), là căn bậc hai số học của phương sai.

Lời giải:

Ta có bảng sau:

Cỡ mẫu là n = 13 + 45 + 24 + 12 + 6 = 100.

Số trung bình của mẫu số liệu ghép nhóm là: 

Bài 2 trang 82 SGK Toán 12 Tập 1 Chân trời sáng tạo

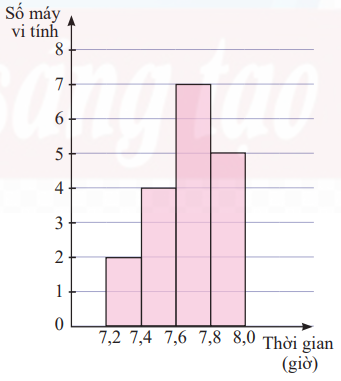
Kết quả khảo sát thời gian sử dụng liên tục (đơn vị: giờ) từ lúc sạc đầy cho đến khi hết của pin một số máy vi tính cùng loại được mô tả bằng biểu đồ bên.

a) Hãy cho biết có bao nhiêu máy vi tính có thời gian sử dụng pin từ 7,2 đến dưới 7,4 giờ?

b) Hãy xác định số trung bình và độ lệch chuẩn của thời gian sử dụng pin.

Phương pháp:

a) Quan sát đồ thị

b) Tính giá trị đại diện

Phương sai của mẫu số liệu ghép nhóm, kí hiệu \({S^2}\), được tính bởi công thức:

\({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}]\)

Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu

\(\overline x  = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k})\) là số trung bình

Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu \(S\), là căn bậc hai số học của phương sai.

Lời giải:

Bài 3 trang 83 SGK Toán 12 Tập 1 Chân trời sáng tạo

Tốc độ của 20 xe hơi khi đi qua một trạm kiểm tra tốc độ (đơn vị: km/h) được thống kê lại như sau:

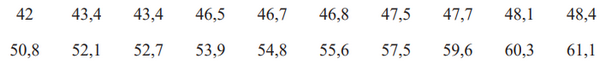
a) Hãy tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của mẫu số liệu trên.
b) Hãy lập bảng tần số ghép nhóm với nhóm đầu tiên là [42; 46) và độ dài mỗi nhóm bằng 4.
c) Hãy tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của mẫu số liệu ghép nhóm.

Phương pháp:

a) Khoảng biến thiên của mẫu số liệu là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu

Tìm trung vị \({Q_2}\)

Tìm trung vị của nửa số liệu bên trái \({Q_2}\), ta được \({Q_1}\)

Tìm trung vị của nửa số liệu bên phải \({Q_2}\), ta được \({Q_3}\)

Khoảng tứ phân vị của mẫu số liệu là hiệu giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu

Phương sai của mẫu số liệu ghép nhóm, kí hiệu \({S^2}\), được tính bởi công thức:

\({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}]\)

Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu

\(\overline x  = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k})\) là số trung bình

Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu \(S\), là căn bậc hai số học của phương sai.

c) Khoảng biến thiên của mẫu số liệu ghép nhóm là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên có chứa dữ liệu của mẫu số liệu.

Tứ phân vị thứ k, kí hiệu là \({Q_k}\), với k = 1, 2, 3 của mẫu số liệu ghép nhóm được xác định như sau:

\({Q_k} = {u_m} + \frac{{\frac{{kn}}{4} - C}}{{{n_m}}}({u_{m + 1}} - {u_m})\)

trong đó:

\(n = {n_1} + {n_2} + {n_3} + ... + {n_k}\) là cỡ mẫu

\([{u_m};{u_{m + 1}}]\) là nhóm chứa tứ phân vị thứ k

\({n_m}\) là tần số của nhóm chứa tứ phân vị thứ k

\(C = {n_1} + {n_2} + {n_3} + ... + {n_{m - 1}}\)

Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu \({\Delta _Q}\), là hiệu giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\).

Tính giá trị đại diện

Phương sai của mẫu số liệu ghép nhóm, kí hiệu \({S^2}\), được tính bởi công thức:

\({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}]\)

Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu

\(\overline x  = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k})\) là số trung bình

Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu \(S\), là căn bậc hai số học của phương sai.

Lời giải:

a) Mẫu số liệu đã cho đã được xếp theo thứ tự không giảm.

Khoảng biến thiên của mẫu số liệu là:

R = 61,1 – 42 = 19,1 (km/h).

Cỡ mẫu n = 20.

Tứ phân vị thứ nhất là trung vị của mẫu số liệu:

42 43,4 43,4 46,5 46,7 46,8 47,5 47,7 48,1 48,4

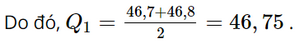
Tứ phân vị thứ ba là trung vị của mẫu số liệu:

50,8 52,1 52,7 53,9 54,8 55,6 57,5 59,6 60,3 61,1

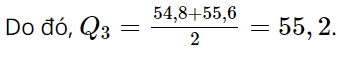
Khoảng tứ phân vị của mẫu số liệu là:

∆Q = Q3 – Q1 = 55,2 – 46,75 = 8,45.

Số trung bình của mẫu số liệu là:

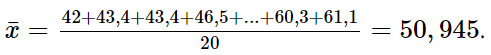
Phương sai của mẫu số liệu là:

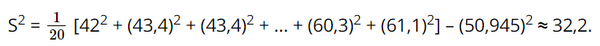
Độ lệch chuẩn của mẫu số liệu là:

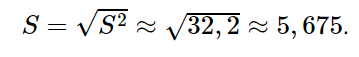
b) Ta lập được bảng tần số ghép nhóm như sau:

c) Khoảng biến thiên của mẫu số liệu ghép nhóm là:

R' =62 – 42 = 20 (km/h).

Gọi x1; x2; …; x20 là mẫu số liệu gốc về tốc độ của 20 xe hơi đi qua một trạm kiểm tra tốc độ được xếp theo thứ tự không giảm.

Ta có x1; x2; x3 ∈ [42; 46), x4; …; x10 ∈ [46; 50), x11; …; x14 ∈ [50; 54),

   x15; …; x17 ∈ [54; 58), x18; x19; x20 ∈ [58; 62).

Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

Từ bảng tần số ghép nhóm, ta có bảng sau:

Số trung bình của mẫu số liệu ghép nhóm là:

Bài 4 trang 83 SGK Toán 12 Tập 1 Chân trời sáng tạo

Một giống cây xoan đào được trồng tại hai địa điểm A và B. Người ta thống kê đường kính thân của một số cây xoan đào 5 năm tuổi ở bảng sau:

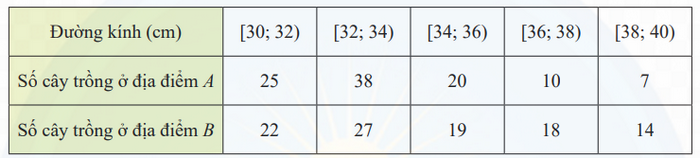
a) Hãy so sánh đường kính trung bình củathân cây xoan đào trồng tại địa điểm A và địa điểm B.

b) Nếu so sánh theo độ lệch chuẩn thì cây trồng tại địa điểm nào có đường kính đồng đều hơn?

Phương pháp:

a) Tính giá trị đại diện

Số trung bình: \(\overline x  = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k})\)

b) Phương sai của mẫu số liệu ghép nhóm, kí hiệu \({S^2}\), được tính bởi công thức:

\({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}]\)

Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu

\(\overline x \) là số trung bình

Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu \(S\), là căn bậc hai số học của phương sai.

Lời giải:

a) Ta có bảng sau:

Cỡ mẫu: nA = 25 + 38 + 20 + 10 + 7 = 100; nB = 22 + 27 + 19 + 18 + 14 = 100.

Đường kính trung bình của thân cây xoan đào trồng tại địa điểm A là: 

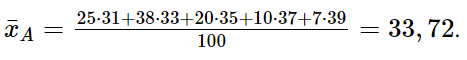
Đường kính trung bình của thân cây xoan đào trồng tại địa điểm B là: 

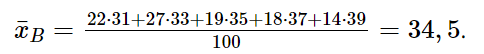
Vì 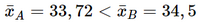 nên đường kính trung bình của thân cây xoan đào trồng tại địa điểm A nhỏ hơn tại địa điểm B.

b) Phương sai của mẫu số liệu ghép nhóm về đường kính của thân cây xoan đào trồng tại địa điểm A là:

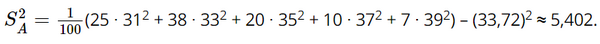
Độ lệch chuẩn mẫu số liệu ghép nhóm về đường kính của thân cây xoan đào trồng tại địa điểm A là:

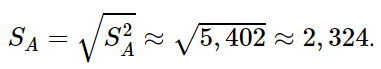
Phương sai của mẫu số liệu ghép nhóm về đường kính của thân cây xoan đào trồng tại địa điểm B là:

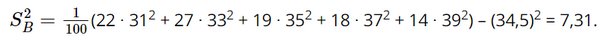
Độ lệch chuẩn mẫu số liệu ghép nhóm về đường kính của thân cây xoan đào trồng tại địa điểm B là:

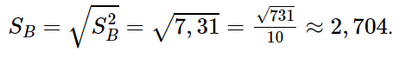
Vì SA ≈ 2,324 < SB ≈ 2,704 nên nếu so sánh theo độ lệch chuẩn thì cây trồng tại địa điểm A có đường kính đồng đều hơn.

Sachbaitap.com