Giải SGK Toán 4 trang 123, 124 Luyện tập chung - 2
Giải bài 1, 2 trang 123, bài 3, 4, 5 trang 124 sách giáo khoa (SGK) Toán lớp 4 tập 2, bài luyện tập chung - 2. Bài 1. Tìm chữ số thích hợp để viết vào chỗ chấm sao cho: a) 75... chia hết cho 2 nhưng không chia hết cho 5.
Bài 1 trang 123 SGK Toán 4 tập 2
Câu hỏi:
Tìm chữ số thích hợp để viết vào chỗ chấm sao cho:
a) 75... chia hết cho 2 nhưng không chia hết cho 5.
b) 75... chia hết cho 2 và chia hết cho 5.
Số tìm được có chia hết cho 3 không?
c) 75... chia hết cho 9
Số tìm được có chia hết cho 2 và 3 không?
Lời giải:
a) Có thể viết vào chỗ chấm một trong các chữ số: 2; 4; 6; 8 tức là: 752, 754, 756, 758
b) Số chia hết cho 2 và chia hết cho 5 thì chữ số tận cùng của số đó phải là 0. Vậy viết 0 vào chỗ chấm: 750
Ta có: 7 + 5 + 0 = 12; 12 chia hết cho 3.
Vậy số 750 là số chia hết cho 3.
c) Để số 75... chia hết cho 9 thì 7 + 5 + ... phải chia hết cho 9, hay 12 + ... phải chia hết cho 9.
Vậy ta điền số 6 vào chỗ chấm: 756
Số 756 có chữ số tận cùng là 6 nên chia hết cho 2, số 756 chia hết cho 3 (vì số 756 có tổng các chữ số là 18 và 18 chia hết cho 3).
Vậy số 756 chia hết cho cả 2 và 3.
Bài 2 trang 123 SGK Toán 4 tập 2
Câu hỏi:
Mỗi lớp học có 14 học sinh trai và 17 học sinh gái.
a) Viết phân số chỉ phần học sinh trai trong số học sinh của lớp học đó.
b) Viết phân số chỉ phần học sinh gái trong số học sinh của lớp học đó.
Lời giải:
Số học sinh của lớp học đó là :
14 + 17 = 31 (học sinh)
a) Phân số chỉ phần học sinh trai trong số học sinh của lớp học đó là: \(\dfrac{14}{31}\).
b) Phân số chỉ phần học sinh gái trong số học sinh của lớp học đó là: \(\dfrac{17}{31}\).
Bài 3 trang 124 SGK Toán 4 tập 2
Câu hỏi:
Trong các phân số \( \dfrac{20}{36}; \;\dfrac{15}{18} ; \;\dfrac{45}{25}; \;\dfrac{35}{63}\) phân số nào bằng \(\dfrac{5}{9}\)?
Lời giải:
Rút gọn các phân số đã cho, ta có:
\(\dfrac{20}{36}=\dfrac{20:4}{36:4}=\dfrac{5}{9}\); \(\dfrac{15}{18}=\dfrac{15:3}{18:3}=\dfrac{5}{6}\)
\(\dfrac{45}{25}=\dfrac{45:5}{25:5}=\dfrac{9}{5}\); \(\dfrac{35}{63}=\dfrac{35:7}{63:7}=\dfrac{5}{9}\)
Vậy các phân số bằng \(\dfrac{5}{9}\) là: \(\dfrac{20}{36};\dfrac{35}{63}\).
Bài 4 trang 124 SGK Toán 4 tập 2
Câu hỏi:
Viết các phân số: \(\dfrac{8}{12};\dfrac{12}{15};\dfrac{15}{20}\) theo thứ tự từ lớn đến bé.
Lời giải:
Rút gọn các phân số:
\(\dfrac{8}{12}=\dfrac{8:4}{12:4}=\dfrac{2}{3}\); \(\dfrac{12}{15}=\dfrac{12:3}{15:3}=\dfrac{4}{5}\); \(\dfrac{15}{20}=\dfrac{15:5}{20:5}=\dfrac{3}{4}\)
Quy đồng mẫu số các phân số: \(\dfrac{2}{3};\dfrac{4}{5};\dfrac{3}{4}\) ta có:
\(\dfrac{2}{3}=\dfrac{2 \times 5 \times 4}{3 \times 5 \times 4}=\dfrac{40}{60}\); \(\dfrac{4}{5}=\dfrac{4 \times 3 \times 4}{5 \times 3 \times 4}=\dfrac{48}{60}\); \(\dfrac{3}{4}=\dfrac{3 \times 3 \times 5}{4 \times 3 \times 5}=\dfrac{45}{60}\)
Vì \( \dfrac{48}{60}> \dfrac{45}{60}>\dfrac{40}{60}\) nên \(\dfrac{4}{5} >\dfrac{3}{4}>\dfrac{2}{3}\).
Hay \(\dfrac{12}{15}> \dfrac{15}{20}> \dfrac{8}{12}\).
Vậy các phân số đã cho xếp theo thứ tự từ lớn đến bé như sau: \(\dfrac{12}{15};\;\dfrac{15}{20};\;\dfrac{8}{12}\).
Bài 5 trang 124 SGK Toán 4 tập 2
Câu hỏi:
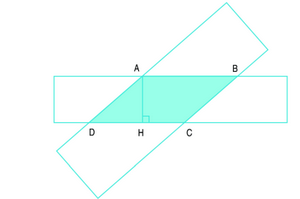
Hai hình chữ nhật có phần chung là hình tứ giác ABCD (xem hình vẽ).
a) Giải thích tại sao hình tứ giác ABCD có từng cặp cạnh đối diện song song.
b) Đo độ dài các cạnh của hình tứ giác ABCD rồi nhận xét xem từng cặp cạnh đối diện có bằng nhau không?
c) Cho biết hình tứ giác ABCD là hình bình hành có độ dài đáy DC là 4cm, chiều cao AH là 2cm. Tính diện tích của hình bình hành ABCD.
Lời giải:
a) Cạnh AB và cạnh DC của tứ giác ABCD thuộc hai cạnh đối diện của hình chữ nhật nằm ngang nên chúng song song với nhau.
Cạnh DA và cạnh BC thuộc hai cạnh đối diện của hình hình chữ nhật đặt chéo nên chúng song song nhau.
b) Đo độ dài các cạnh của hình tứ giác ABCD ta có:
AB = 4cm; DA = 3cm;
CD = 4cm; BC = 3cm
Do đó AB = CD và DA = BC.
Vậy tứ giác ABCD có từng cặp cạnh đối diện bằng nhau.
c) Diện tích hình bình hành ABCD là:
4 × 2 = 8 (cm2)
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài 1, 2, 3, 4 trang 104, 105 SGK Toán lớp 4 - Luyện tập (26/04)
- Bài 1, 2, 3 trang 104 SGK Toán lớp 4 - Diện tích hình bình hành (26/04)
- Bài 1, 2, 3 trang 102, 103 SGK Toán lớp 4 - Hình bình hành (26/04)
- Bài 1, 2, 3, 4, 5 trang 100, 101 SGK Toán lớp 4 - Luyện tập (26/04)
- Bài 1, 2, 3, 4 trang 100 SGK Toán lớp 4 - Ki-lô-mét vuông (25/04)
- CHƯƠNG VI: ÔN TẬP
- CHƯƠNG V: TỈ SỐ - MỘT SỐ BÀI TOÁN LIÊN QUAN ĐẾN TỈ SỐ. TỈ LỆ BẢN ĐỒ
- CHƯƠNG IV: PHÂN SỐ - CÁC PHÉP TÍNH VỚI PHÂN SỐ. GIỚI THIỆU HÌNH THOI
- CHƯƠNG III: DẤU HIỆU CHIA HẾT CHO 2, 5, 9, 3. GIỚI THIỆU HÌNH BÌNH HÀNH
- CHƯƠNG II: BỐN PHÉP TÍNH VỚI CÁC SỐ TỰ NHIÊN. HÌNH HỌC
- CHƯƠNG I: SỐ TỰ NHIÊN. BẢNG ĐƠN VỊ ĐO KHỐI LƯỢNG
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
