Giải SGK Toán 4 trang 134 Luyện tập (tiếp)
Giải 1, 2, 3 trang 134 sách giáo khoa (SGK) Toán lớp 4 tập 2, luyện tập (tiếp). Bài 2. Tính chu vi hình chữ nhật có chiều dài 4/5 m và chiều rộng 2/3 m.
Bài 1 trang 134 SGK Toán 4 tập 2
Câu hỏi:
a) Viết tiếp vào chỗ chấm:
+) Nhận xét: \( \displaystyle{2 \over 3} \times {4 \over 5} = \;...;\) \( \displaystyle{4 \over 5} \times {2 \over 3} =\; ...\)
Vậy: \( \displaystyle{2 \over 3} \times {4 \over 5} \cdots {4 \over 5} \times {2 \over 3}.\)
Tính chất giao hoán: Khi đổi chỗ các phân số trong một tích thì tích của chúng không thay đổi.
+) Nhận xét: \( \displaystyle\left( {{1 \over 3} \times {2 \over 5}} \right) \times {3 \over 4} = \cdots \)
\( \displaystyle{1 \over 3} \times \left( {{2 \over 5} \times {3 \over 4}} \right) = \cdots \)
Vậy: \( \displaystyle\left( {{1 \over 3} \times {2 \over 5}} \right) \times {3 \over 4} \cdots {1 \over 3} \times \left( {{2 \over 5} \times {3 \over 4}} \right)\)
Tính chất kết hợp: Khi nhân một tích hai phân số với phân số thứ ba, ta có thể nhân phân số thứ nhất với tích của phân số thứ hai và phân số thứ ba.
+) Nhận xét: \( \displaystyle\left( {{1 \over 5} + {2 \over 5}} \right) \times {3 \over 4} = \cdots ;\)
\( \displaystyle{1 \over 5} \times {3 \over 4} + {2 \over 5} \times {3 \over 4} = \cdots \)
Vậy: \( \displaystyle\left( {{1 \over 5} + {2 \over 5}} \right) \times {3 \over 4} \cdots {1 \over 5} \times {3 \over 4} + {2 \over 5} \times {3 \over 4}\)
Khi nhân một tổng hai phân số với phân số thứ ba, ta có thể nhân từng phân số của tổng với phân số thứ ba rồi cộng các kết quả lại.
b) Tính bằng hai cách:
\( \displaystyle{3 \over {22}} \times {3 \over {11}} \times 22;\) \( \displaystyle\left( {{1 \over 2} + {1 \over 3}} \right) \times {2 \over 5};\)
\( \displaystyle{3 \over 5} \times {{17} \over {21}} + {{17} \over {21}} \times {2 \over 5}.\)
Lời giải:
a) \(+)\) \( \displaystyle \displaystyle{2 \over 3} \times {4 \over 5} = {{2 \times 4} \over {3 \times 5}} = {8 \over {15}}\)
\( \displaystyle \displaystyle{4 \over 5} \times {2 \over 3} = {{4 \times 2} \over {5 \times 3}} = {8 \over {15}}\)
Vậy: \( \displaystyle \displaystyle{2 \over 3} \times {4 \over 5}= {4 \over 5} \times {2 \over 3}\)
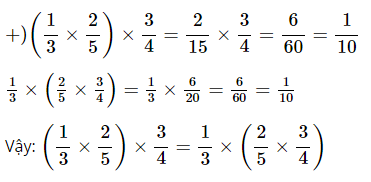
Vậy: \( \displaystyle \displaystyle\left( {{1 \over 3} \times {2 \over 5}} \right) \times {3 \over 4} = {1 \over 3} \times \left( {{2 \over 5} \times {3 \over 4}} \right)\)
\(+)\) \( \displaystyle \displaystyle\left( {{1 \over 5} + {2 \over 5}} \right) \times {3 \over 4} = {3 \over 5} \times {3 \over 4} = {{3 \times 3} \over {5 \times 4}} \) \( \displaystyle= {9 \over {20}}\)
\( \displaystyle \displaystyle{1 \over 5} \times {3 \over 4} + {2 \over 5} \times {3 \over 4} = {{1 \times 3} \over {5 \times 4}} + {{2 \times 3} \over {5 \times 4}} \)
\( \displaystyle \displaystyle= {3 \over {20}} + {6 \over {20}} \) \( \displaystyle \displaystyle= {{3 + 6} \over {20}} = {9 \over {20}}\)
Vậy: \( \displaystyle \displaystyle\left( {{1 \over 5} + {2 \over 5}} \right) \times {3 \over 4} = {1 \over 5} \times {3 \over 4} + {2 \over 5} \times {3 \over 4}\)
b)
1) \( \displaystyle \displaystyle{3 \over {22}} \times {3 \over {11}} \times 22;\)
Cách 1:
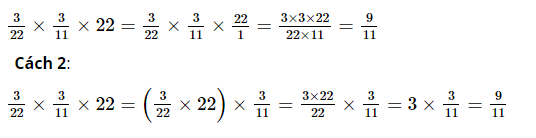
2) \( \displaystyle \displaystyle\left( {{1 \over 2} + {1 \over 3}} \right) \times {2 \over 5};\)
Cách 1:
\( \displaystyle \displaystyle\left( {{1 \over 2} + {1 \over 3}} \right) \times {2 \over 5} \) \( \displaystyle \displaystyle= \left( {{3 \over 6} + {2 \over 6}} \right) \times {2 \over 5} = {5 \over 6} \times {2 \over 5} \) \( \displaystyle \displaystyle= {2 \over 6} = {1 \over 3}\)
Cách 2:
\( \displaystyle \displaystyle\left( {{1 \over 2} + {1 \over 3}} \right) \times {2 \over 5} = {1 \over 2} \times {2 \over 5} + {1 \over 3} \times {2 \over 5} \)\( \displaystyle = {1 \over 5} + {2 \over {15}} \) \( \displaystyle \displaystyle= {3 \over {15}} + {2 \over {15}} = {5 \over {15}} = {1 \over 3}\)
3) \( \displaystyle \displaystyle{3 \over 5} \times {{17} \over {21}} + {{17} \over {21}} \times {2 \over 5}\)
Cách 1:
\( \displaystyle \displaystyle{3 \over 5} \times {{17} \over {21}} + {{17} \over {21}} \times {2 \over 5} \) \( \displaystyle = {{51} \over {105}} + {{34} \over {105}} \)\( \displaystyle \displaystyle= {{85} \over {105}} = {{17} \over {21}}\)
Cách 2:
\( \displaystyle \displaystyle{3 \over 5} \times {{17} \over {21}} + {{17} \over {21}} \times {2 \over 5} = {{17} \over {21}} \times \left( {{3 \over 5} + {2 \over 5}} \right) \) \( \displaystyle \displaystyle= {{17} \over {21}} \times {5 \over 5} \) \( \displaystyle \displaystyle= {{17} \over {21}} \times 1 = {{17} \over {21}}\)
Bài 2 trang 134 SGK Toán 4 tập 2
Câu hỏi:
Tính chu vi hình chữ nhật có chiều dài \( \displaystyle{{4} \over {5}}m\) và chiều rộng \( \displaystyle \displaystyle{{2} \over {3}}m\).
Lời giải:
Chu vi hình chữ nhật là:
\( \displaystyle \left( {{4 \over 5} + {2 \over 3}} \right) \times 2 = {{44} \over {15}}\;(m)\)
Đáp số: \( \displaystyle \displaystyle{{44} \over {15}}m\).
Bài 3 trang 134 SGK Toán 4 tập 2
Câu hỏi:
May một chiếc túi hết \( \displaystyle {{2} \over {3}}m\) vải. Hỏi may \(3\) chiếc túi như thế hết mấy mét vải ?
Lời giải:
Tóm tắt:
Một chiếc túi: \( \displaystyle {{2} \over {3}}m\) vải
3 chiếc túi: ... mét vài?
Bài giải:
Số vải để may \(3\) cái túi là:
\( \displaystyle {2 \over 3} \times 3 = 2\;(m)\)
Đáp số: \(2m\).
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài 1, 2, 3, 4 trang 104, 105 SGK Toán lớp 4 - Luyện tập (26/04)
- Bài 1, 2, 3 trang 104 SGK Toán lớp 4 - Diện tích hình bình hành (26/04)
- Bài 1, 2, 3 trang 102, 103 SGK Toán lớp 4 - Hình bình hành (26/04)
- Bài 1, 2, 3, 4, 5 trang 100, 101 SGK Toán lớp 4 - Luyện tập (26/04)
- Bài 1, 2, 3, 4 trang 100 SGK Toán lớp 4 - Ki-lô-mét vuông (25/04)
- CHƯƠNG VI: ÔN TẬP
- CHƯƠNG V: TỈ SỐ - MỘT SỐ BÀI TOÁN LIÊN QUAN ĐẾN TỈ SỐ. TỈ LỆ BẢN ĐỒ
- CHƯƠNG IV: PHÂN SỐ - CÁC PHÉP TÍNH VỚI PHÂN SỐ. GIỚI THIỆU HÌNH THOI
- CHƯƠNG III: DẤU HIỆU CHIA HẾT CHO 2, 5, 9, 3. GIỚI THIỆU HÌNH BÌNH HÀNH
- CHƯƠNG II: BỐN PHÉP TÍNH VỚI CÁC SỐ TỰ NHIÊN. HÌNH HỌC
- CHƯƠNG I: SỐ TỰ NHIÊN. BẢNG ĐƠN VỊ ĐO KHỐI LƯỢNG
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
