Giải Toán 7 trang 46 Kết nối tri thức với cuộc sống tập 2

Bài 7.42 trang 46 SGK Toán 7 tập 2 - Kết nối tri thức

Một hãng taxi quy định giá cước như sau: 0,5 km đầu tiên giá 8 000 đồng; tiếp theo cứ mỗi kilomet giá 11 000 đồng. Giả sử một người thuê xe đi x (km)

a) Chứng tỏ rằng biểu thức biểu thị số tiền mà người đó phải trả là một đa thức. Tìm bậc, hệ số cao nhất và hệ số tự do của đa thức đó.

b) Giá trị của đa thức tại x = 9 nói lên điều gì?

Phương pháp:

a) Tìm đa thức biểu thị số tiền mà người đó phải trả:

T = số tiền đi 0,5 km đầu tiên + số tiền đi x – 0,5 km tiếp theo.

+ Bậc của đa thức là bậc của hạng tử có bậc cao nhất

+ Hệ số cao nhất là hệ số của hạng tử có bậc cao nhất

+ Hệ số tự do là hệ số của hạng tử bậc 0.

b) Thay x = 9 vào đa thức, tìm giá trị của đa thức

Lời giải:

a) Biểu thức biểu thị số tiền mà người đó phải trả:

T(x)=8000+11000(x–0,5)=11000x–5500+8000

=> T(x)=11000x+2500

• Bậc: 1
• Hệ số cao nhất: 11000
• Hệ số tự do: 4000

b) Thay x=9 vào đa thức T(x) ta được: 

T(9)=11000.9+2500=101500

* Vậy: Giá trị của đa thức tại x=9 nói lên rằng nếu người đó thuê xe đi 9 km thì số tiền phải trả là 101500 đồng.

Bài 7.43 trang 46 SGK Toán 7 tập 2 - Kết nối tri thức

Cho đa thức bậc hai F(x) = ax² + bx + c, trong đó, a,b và c là những số với a \( \ne \) 0

a) Cho biết a + b + c = 0. Giải thích tại sao x = 1 là một nghiệm của F(x)

b) Áp dụng, hãy tìm một nghiệm của đa thức bậc hai 2x² – 5x + 3

Phương pháp:

Giá trị x = m là 1 nghiệm của đa thức P(x) khi P(m) = 0

Lời giải:

a) Xét x = 1, ta có:

Theo đề bài, a+b+c=0 nên x=1 là nghiệm của đa thức F(x).

b) Ta thấy đa thức  có:

a=2; b=−5; c=3

Mà a+b+c=0

* Vậy: đa thức  có:

• Một nghiệm bằng 1.
• Nghiệm còn lại là 

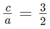
Bài 7.44 trang 46 SGK Toán 7 tập 2 - Kết nối tri thức

Cho đa thức A = x⁴ + x³ – 2x – 2

a) Tìm đa thức B sao cho A + B = x³ + 3x + 1

b) Tìm đa thức C sao cho A – C = x⁵

c) Tìm đa thức D biết rằng D = (2x³ – 3) . A

d) Tìm đa thức P sao cho A = (x+1) . P

e) Có hay không một đa thức Q sao cho A = (x² + 1) . Q?

Phương pháp:

* Cách cộng (trừ) 2 đa thức:

Cách 1: Bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc.

Cách 2: Đặt tính cộng (trừ) sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng ( trừ) theo từng cột.

* Cách nhân 2 đa thức:

Cách 1: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau

Cách 2: Đặt tính nhân:

+ Nhân lần lượt mỗi hạng tử ở dòng dưới với đa thức ở dòng trên và viết kết quả trng một dòng riêng.

+ Viết các dòng sao cho các hạng tử cùng bậc thẳng cột với nhau để thực hiện phép cộng theo cột.

*  Muốn chia đa thức A cho đa thức B, ta làm như sau:

Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B.

Bước 2: Lấy A trừ đi tích của B với thương mới thu được ở bước 1

Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B

Bước 4: Lấy dư thứ nhất trừ đi tích B với thương vừa thu được ở bước 3

Bước 5: Làm tương tự như trên

Đến khi dư cuối cùng có bậc nhỏ hơn bậc của B thì quá trình chia kết thúc.

Lời giải:

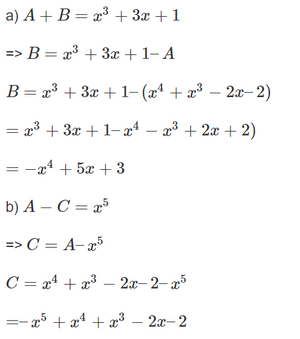
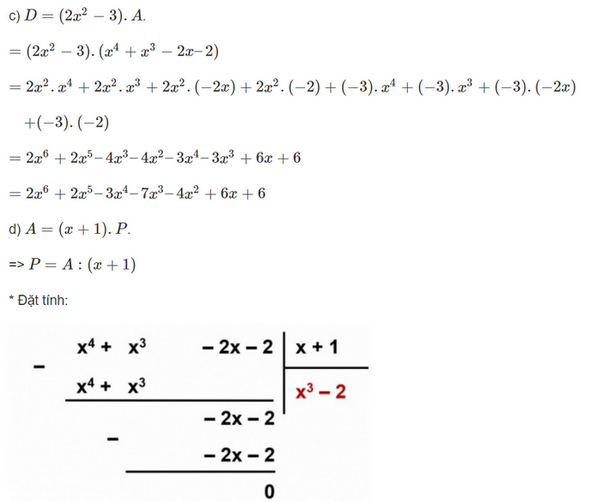
Bài 7.45 trang 46 SGK Toán 7 tập 2 - Kết nối tri thức

Cho đa thức P(x). Giải thích tại sao nếu có đa thức Q(x) sao cho P(x) = (x – 3) . Q(x) (tức là P(x) chia hết cho x – 3) thì x = 3 là một nghiệm của P(x)

Phương pháp:

Nghiệm của đa thức biến x là giá trị của x mà tại đó, đa thức có giá trị bằng 0.

Lời giải:

P(x)=(x−3).Q(x)

Để P(x) = 0thì:Q(x) = 0 hoặc (x−3)=0

- Ta có: x–3=0 => x=3

=> Nếu x=3 thì P(x)=0

* Vậy: x=3 là một nghiệm của P(x).

Bài 7.46 trang 46 SGK Toán 7 tập 2 - Kết nối tri thức

Hai bạn Tròn và Vuông tranh luận với nhau như sau:

Hãy cho biết ý kiến của em và nêu một ví dụ minh họa.

Phương pháp:

Tổng của các đa thức là đa thức có bậc không lớn hơn bậc của các đa thức thành phần

Lời giải:

Sachbaitap.com