Giải Toán 7 trang 53, 54 Kết nối tri thức với cuộc sống tập 1

Bài 3.17 trang 53 SGK Toán 7 tập 1 - Kết nối tri thức

Cho Hình 3.39, biết rằng mn//pq. Tính số đo các góc Mhk, VHn.

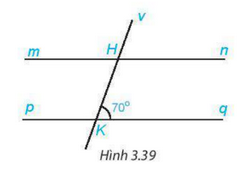
Phương pháp:

Sử dụng tính chất: Nếu 1 đường thẳng cắt hai đường thẳng song song thì:

Hai góc so le trong bằng nhau

Hai góc đồng vị bằng nhau

Lời giải:

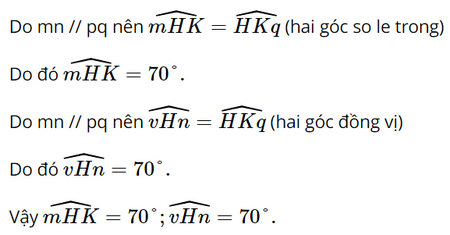
Bài 3.18 trang 53 SGK Toán 7 tập 1 - Kết nối tri thức

Cho Hình 3.40

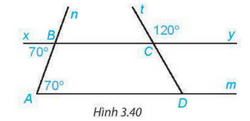
a) Giải thích tại sao Am//By.

b) Tính \(\widehat {CDm}\)

Phương pháp:

a) Sử dụng dấu hiệu nhận biết 2 đường thẳng song song.

b) Sử dụng tính chất của 2 đường thẳng song song

Lời giải:

a) Ta có 

Mà hai góc này ở vị trí so le trong nên Am // Bx hay Am // By (dấu hiệu nhận biết hai đường thẳng song song).

b) Do Am // By nên  (hai góc đồng vị) nên 

Vậy 

Bài 3.19 trang 54 SGK Toán 7 tập 1 - Kết nối tri thức

Cho Hình 3.41.

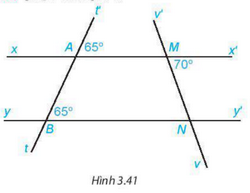
a) Giải thích tại sao xx’//yy’.

b) Tính số đo góc MNB.

Phương pháp:

a) Sử dụng dấu hiệu nhận biết 2 đường thẳng song song.

b) Sử dụng tính chất của 2 đường thẳng song song

Lời giải:

a) Vì \(\widehat {t'AM} = \widehat {ABN}( = 65^\circ )\), mà 2 góc này ở vị trí đồng vị nên xx’//yy’ ( Dấu hiệu nhận biết 2 đường thẳng song song.)

b) Vì xx’//yy’ nên \(\widehat {x'MN} = \widehat {MNB}\)( 2 góc so le trong), mà \(\widehat {x'MN} = 70^\circ  \Rightarrow \widehat {MNB} = 70^\circ \)

Bài 3.20 trang 54 SGK Toán 7 tập 1 - Kết nối tri thức

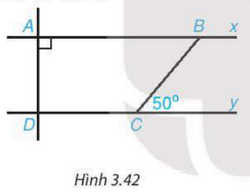
Cho Hình 3.42, biết rằng Ax//Dy, \(\widehat A = 90^\circ ,\widehat {BCy} = 50^\circ \). Tính số đo các góc ADC và ABC.

Phương pháp:

Sử dụng tính chất: Nếu 1 đường thẳng cắt hai đường thẳng song song thì:

Hai góc so le trong bằng nhau

Hai góc đồng vị bằng nhau

Lời giải:

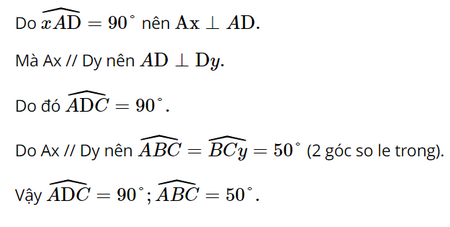
Bài 3.21 trang 54 SGK Toán 7 tập 1 - Kết nối tri thức

Cho Hình 3.43. Giải thích tại sao:

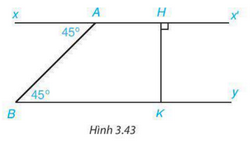
a) Ax’ // By     b) By \( \bot \) HK

Phương pháp:

a) Sử dụng dấu hiệu nhận biết 2 đường thẳng song song.

b) Sử dụng tính chất đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì vuông góc với đường thẳng kia

Lời giải:

Bài 3.22 trang 54 SGK Toán 7 tập 1 - Kết nối tri thức

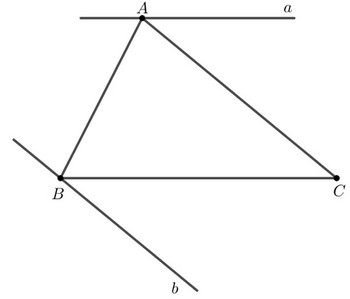
Cho tam giác ABC. Vẽ đường thẳng a đi qua A và song song với BC. Vẽ đường thẳng b đi qua B và song song với AC. Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thằng b? Vì sao?

Phương pháp:

Dựa vào tiên đề Euclid: Qua một điểm nằm ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.

Lời giải:

Qua điểm A nằm ngoài đoạn BC, vẽ được duy nhất một đường thẳng song song với BC. Do đó ta chỉ có thể vẽ được 1 đường thẳng a.

Qua điểm B nằm ngoài đoạn AC, vẽ được duy nhất một đường thẳng song song với AC. Do đó ta chỉ có thể vẽ được 1 đường thẳng b.

Bài 3.23 trang 54 SGK Toán 7 tập 1 - Kết nối tri thức

Cho Hình 3.44. Giải thích tại sao:

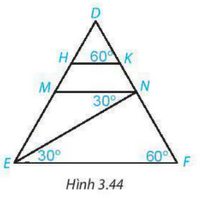
a) MN//EF

b) HK//EF

c) HK//MN

Phương pháp:

Sử dụng dấu hiệu nhận biết 2 đường thẳng song song.

Sử dụng tính chất 2 đường thẳng cùng song song với 1 đường thẳng thứ ba thì chúng song song với nhau.

Lời giải:

a) Ta có 

Mà hai góc này ở vị trí so le trong nên MN // EF (dấu hiệu nhận biết hai đường thẳng song song).

b) Ta có 

Mà hai góc này ở vị trí đồng vị nên HK // EF (dấu hiệu nhận biết hai đường thẳng song song).

c) Do MN // EF và HK // EF nên HK // MN.

Sachbaitap.com