Giải Toán 7 trang 65 Kết nối tri thức với cuộc sống tập 2
Giải bài 9.6, 9.7, 9.8, 9.9 trang 65 SGK Toán lớp 7 tập 2 kết nối tri thức với cuộc sống. Bài 9.6. Chiều cao của tam giác ứng với một cạnh của nó có phải là khoảng cách từ đỉnh đối diện đến đường thẳng chứa cạnh đó không?
Bài 9.6 trang 65 SGK Toán 7 tập 2 - Kết nối tri thức
Chiều cao của tam giác ứng với một cạnh của nó có phải là khoảng cách từ đỉnh đối diện đến đường thẳng chứa cạnh đó không?
Phương pháp:
Độ dài của đường vuông góc kẻ từ 1 điểm đến 1 đường thẳng là khoảng cách từ điểm đó đến đường thẳng.
Lời giải:
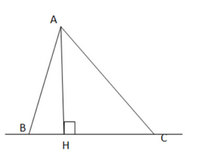
Dựa theo hình thì AH chính là chiều cao của tam giác ABC. AH ⊥ BC và AH là đoạn ngắn nhất so với AB và AC nên AH chính là khoảng cách từ a đến đoạn thẳng BC
Bài 9.7 trang 65 SGK Toán 7 tập 2 - Kết nối tri thức
Cho hình vuông ABCD. Hỏi trong bốn đỉnh của hình vuông
a) Đỉnh nào cách đều hai điểm A và C?
b) Đỉnh nào cách đều hai đường thẳng AB và AD?
Phương pháp:
a) Tìm đỉnh cách đều hai điểm A và C
b) Tìm đỉnh mà đường vuông góc kẻ từ đỉnh đó xuống hai đường thẳng AB và AD bằng nhau.
Lời giải:
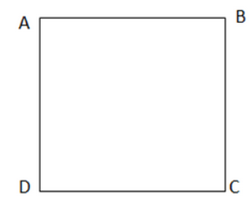
a) Đỉnh B và đỉnh D
b) Đỉnh C
Bài 9.8 trang 65 SGK Toán 7 tập 2 - Kết nối tri thức
Cho tam giác cân ABC, AB = AC. Lấy điểm M tùy ý nằm giữa B và C. ( H. 9.12)
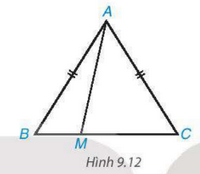
a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM nhỏ nhất.
b) Chứng minh rằng với mọi điểm M thì AM < AB
Phương pháp:
Sử dụng định lí:
+ Trong các đường xiên và đường vuông góc kẻ từ 1 điểm nằm ngoài 1 đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.
+ Trong một tam giác, cạnh đối diện với góc lớn nhất là cạnh lớn nhất.
Lời giải:
a)
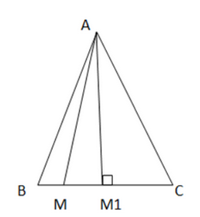
Gọi M1 là trung điểm của cạnh đáy BC. Suy ra AM1 ⊥ BC. AM1 chính là khoảng cách từ A đến BC
Theo định lí về đường xiên và đường vuông góc thì AM1 chính là đường ngắn nhất trong tam giác ABC
Vậy nếu M là trung điểm của BC thì AM sẽ có độ dài nhỏ nhất
b) Khi M nằm giữa C và B
Nếu BM < MC thì ta sẽ được góc tù ![]() . Theo định lý về góc và cạnh đối diện, AB sẽ lớn hơn AM
. Theo định lý về góc và cạnh đối diện, AB sẽ lớn hơn AM
Tương tự khi BM>MC. ta sẽ được góc tù ![]() . Theo định lý về góc và cạnh đối diện, AC sẽ lớn hơn AM
. Theo định lý về góc và cạnh đối diện, AC sẽ lớn hơn AM
Mà AB=AC. Suy ra, bất cứ điểm nào nằm giữa B và C, AM luôn bé hơn AB
Bài 9.9 trang 65 SGK Toán 7 tập 2 - Kết nối tri thức
Cho tam giác ABC vuông tại A. Hai điểm M, N theo thứ tự nằm trên các cạnh AB, AC ( M,N không phải là đỉnh của tam giác) (H. 9.13) . Chứng minh rằng MN < BC.
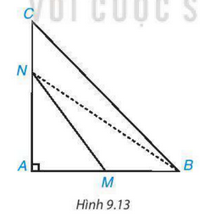
Phương pháp:
Sử dụng:
+ Góc tù là góc lớn nhất trong tam giác
+ Trong một tam giác, cạnh đối diện với góc lớn nhất là cạnh lớn nhất
Lời giải:
- Nối N với B
- NA là đường vuông góc từ điểm N xuống đoạn AN và AB
- NB là đường xiên, AB là hình chiếu của NB. NM là hình xiên, AM là hình chiếu của NM
AM < AB=> NM < NB
- Tương tự, AC là hình chiếu của đường xiên BC, AN là hình chiếu của đường xiên NB
AN< AC=> NB<BC
Từ đó ta thấy NM<BC
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải Toán 7 trang 102 Kết nối tri thức với cuộc sống tập 2 (30/08)
- Giải Toán 7 trang 101 Kết nối tri thức với cuộc sống tập 2 (30/08)
- Giải Toán 7 trang 98, 99 Kết nối tri thức với cuộc sống tập 2 (30/08)
- Giải Toán 7 trang 93 Kết nối tri thức với cuộc sống tập 2 (30/08)
- Giải Toán 7 trang 90, 91 Kết nối tri thức với cuộc sống tập 2 (30/08)
- Bài tập cuối chương X
- Luyện tập trang 100
- Bài 37. Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác
- Luyện tập trang 92
- Bài 36. Hình hộp chữ nhật và hình lập phương
- Chương X. Một số hình khối trong thực tiễn
- Bài tập cuối chương IX
- Luyện tập chung trang 82
- Bài 35. Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
- Bài 34. Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!