Giải Toán 7 trang 66, 67 Chân trời sáng tạo tập 1
Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9 trang 66, 67 SGK Toán lớp 7 chân trời sáng tạo tập 1. Bài 8. Hãy nêu các bước tạo lập hình lăng trụ đứng tam giác trong Hình 6.
Xem thêm: Bài tập cuối chương 3 - CTST
Bài 1 trang 66 SGK Toán 7 tập 1 - Chân trời sáng tạo
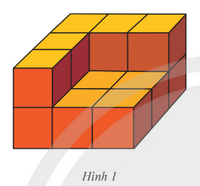
Một hình khối gồm 14 hình lập phương gắn kết với nhau như Hình 1. Mỗi hình lập phương cạnh 1 cm. Hãy tính thể tích của hình khối này.
Phương pháp:
Thể tích khối hình = tổng thể tích của các hình lập phương nhỏ
Thể tích hình lập phương cạnh a là: a3
Lời giải:
Thể tích của mỗi hình lập phương có cạnh 1 cm là:
13 = 1 (cm3)
Thể tích hình khối gồm 14 hình lập phương gắn kết với nhau là:
1 . 14 = 14 (cm3)
Vậy thể tích hình khối gồm 14 hình lập phương gắn kết với nhau là 14 cm3
Bài 2 trang 66 SGK Toán 7 tập 1 - Chân trời sáng tạo
Một bể cá hình hộp chữ nhật với kích thước mặt đáy là 5 dm và 12 dm, có mực nước là 7 dm. Người ta đổ vào đó một lượng cát (có độ thấm nước không đáng kể) thì thấy mực nước dâng thêm 1,5 dm và ngập cát đổ vào. Tính thể tích của lượng cát.
Phương pháp:
Cách 1:
Bước 1: Tính thể tích mực nước ban đầu
Bước 2: Tính thể tích nước và cát sau khi đổ cát
Bước 3: Tính thể tích cát đổ vào = thể tích sau khi đổ cát - thể tích mực nước ban đầu
Cách 2:
Thể tích lượng cát = thể tích hình hộp có kích thước mặt đáy là 5 dm và 12 dm, chiều cao 1,5 dm
Chú ý: Thể tích hình hộp chữ nhật có kích thước a,b,c là: V= a.b.c
Lời giải:
Thể tích lượng nước ban đầu là:
5 . 12 . 7 = 420 (dm3)
Chiều cao mực nước sau khi đổ cát vào bể là:
7 + 1,5 = 8,5 (dm)
Thể tích lượng cát và nước (sau khi đổ cát vào) là:
5 . 12 . 8,5 = 510 (dm3)
Thể tích của lượng cát là:
510 – 420 = 90 (dm3)
Vậy thể tích của lượng cát là 90 dm3
Bài 3 trang 66 SGK Toán 7 tập 1 - Chân trời sáng tạo
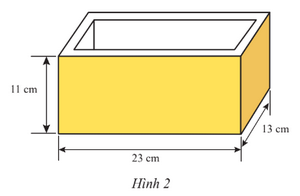
Một khuôn đúc bê tông có kích thước như Hình 2. Bề dày các mặt bên của khuôn là 1,2 cm. Bề dày mặt đáy của khuôn là 1,9 cm. Thể tích của khối bê tông được khuôn này đúc ra là bao nhiêu xăng ti mét khối?
Phương pháp:
Tính chiều dài, chiều rộng, chiều cao của lõi khuôn
Thể tích khối bê tông được khuôn này đúc ra = thể tích lõi khuôn
Chú ý: Lõi khuôn là hình hộp chữ nhật
Lời giải:
Thể tích của hình hộp chữ nhật bao quanh khối bê tông là:
23 . 13 . 11 = 3 289 (cm3)
Phần bên trong của khối bê tông có dạng hình hộp chữ nhật có:
+ Chiều dài: 23 – 2 . 1,2 = 20,6 (cm)
+ Chiều rộng: 13 – 2 . 1,2 = 10,6 (cm)
+ Chiều cao: 11 – 1,9 = 9,1 (cm).
Thể tích phần bên trong của khối bê tông là:
20,6 . 10,6 . 9,1 = 1 987,076 (cm3)
Thể tích của khối bê tông được khuôn này đúc ra là:
3 289 – 1 987,076 = 1 310,924 (cm3)
Vậy thể tích của khối bê tông được khuôn này đúc ra là 1 310,924 (cm3)
Bài 4 trang 66 SGK Toán 7 tập 1 - Chân trời sáng tạo
Phần bên trong của một cái khuôn làm bánh có dạng hình hộp chữ nhật với đáy là hình vuông cạnh 20 cm, chiều cao 5 cm ( Hình 3). Người ta dự định sơn phần bên trong bằng loại sơn không dính. Hỏi với một lượng sơn đủ bao phủ được 100 m2 thì sơn được bao nhiêu cái khuôn làm bánh?

Phương pháp:
Tính diện tích xung quanh của phần bên trong khuôn: Sxq = Cđáy . h
Số khuôn bánh = diện tích bao phủ được : diện tích 1 khuôn
Lời giải:
Đổi: 100 m2 = 1 000 000 cm2
Diện tích xung quanh của cái khuôn làm bánh là:
20 . 4 . 5 = 400 (cm2)
Diện tích đáy của cái khuôn làm bánh là:
202 = 400 (cm2)
Diện tích các mặt cần sơn là:
400 + 400 = 800 (cm2)
Với loại sơn đủ bao phủ được 100 m2 thì sơn được số cái khuôn làm bánh là:
1 000 000 : 800 = 1 250 (cái)
Vậy với loại sơn đủ bao phủ được 100 m2 thì sơn được 1 250 cái khuôn làm bánh.
Bài 5 trang 66 SGK Toán 7 tập 1 - Chân trời sáng tạo
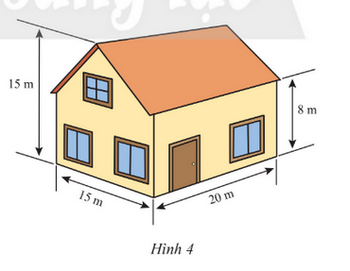
Một ngôi nhà có kích thước như Hình 4.
a) Tính thể tích của ngôi nhà.
b) Biết rằng 1 l sơn bao phủ được 4 m2 tường. Hỏi phải cần ít nhất bao nhiêu lít sơn để sơn phủ được tường mặt ngoài ngôi nhà? (không sơn cửa)? Biết tổng diện tích các cửa là 9 m2.
Phương pháp:
Chia ngôi nhà thành 1 hình hộp chữ nhật và 1 hình lăng trụ tam giác
a) Thể tích ngôi nhà = thể tích hình hộp + thể tích lăng trụ tam giác
b) Diện tích cần sơn = diện tích xung quanh hình hộp + diện tích 2 đáy lăng trụ - diện tích các cửa
Lời giải:
Đơn vị các kích thước của ngôi nhà trong hình vẽ bị sai.
Sửa lại các kích thước của ngôi nhà đều có đơn vị là mét.
Bài 6 trang 67 SGK Toán 7 tập 1 - Chân trời sáng tạo
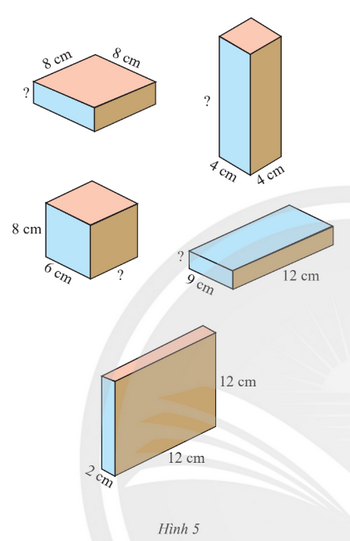
Các hình hộp chữ nhật trong Hình 5 có cùng số đo thể tích. Em hãy tìm các kích thước còn thiếu.
Phương pháp:
Bước 1: Tính thể tích hình hộp = chiều dài. Chiều rộng . chiều cao
Bước 2: Tìm kích thước còn thiếu trong các hình
Lời giải:
Các hình hộp chữ nhật trong Hình 5 có cùng số đo thể tích và đều bằng:
12 . 2 . 12 = 288 (cm3)
Chiều cao của hình hộp chữ nhật thứ nhất là:
288 : (8 . 8) = 4,5 (cm)
Chiều cao của hình hộp chữ nhật thứ hai là:
288 : (4 . 4) = 18 (cm)
Cạnh còn lại của đáy của hình hộp chữ nhật thứ ba là:
288 : (8 . 6) = 6 (cm)
Chiều cao của hình hộp chữ nhật thứ tư là:
![]()
Bài 7 trang 67 SGK Toán 7 tập 1 - Chân trời sáng tạo
Tạo lập hình lăng trụ đứng có chiều cao 2,5 cm, đáy là hình thoi có cạnh 3 cm và một góc \(60^0\)
Phương pháp:
- Vẽ 4 hình chữ nhật với kích thước 3 cm x 2,5 cm
- Gấp các cạnh BN, CP và DQ sao cho cạnh AM trùng với A’M’ , một góc bằng 60, ta được hình lăng trụ đứng ABCD.MNPQ cần tạo lập
Lời giải:
Tạo lập hình lăng trụ đứng tứ giác có chiều cao 2,5 cm, đáy là hình thoi cạnh 3 cm và một góc 60o như sau:
- Vẽ bốn hình chữ nhật và hai hình thoi với kích thước như hình vẽ sau.
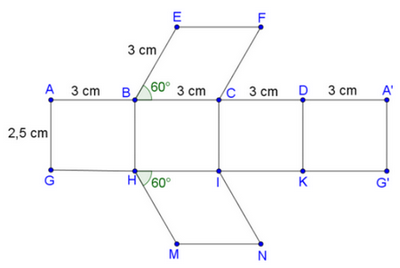
- Gấp các cạnh BH, CI và DK sao cho cạnh AG trùng với A’G’,
- Gấp cạnh BC sao cho cạnh AB trùng với BE, cạnh CD trùng với CF, cạnh EF trùng với DA’.
- Gấp cạnh HI sao cho cạnh GH trùng với HM, cạnh IN trùng với IK, cạnh MN trùng với KG’.
Khi đó, ta được hình lăng trụ đứng tứ giác ABCD.GHIK có chiều cao 2,5 cm, đáy là hình thoi có cạnh 3 cm và một góc 60o (như hình vẽ).
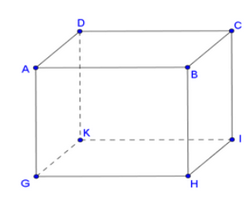
Bài 8 trang 67 SGK Toán 7 tập 1 - Chân trời sáng tạo
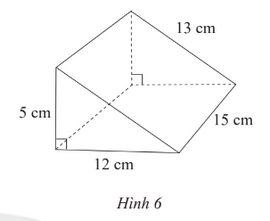
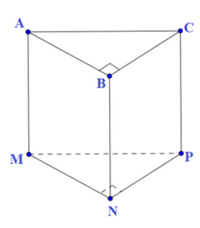
Hãy nêu các bước tạo lập hình lăng trụ đứng tam giác trong Hình 6.
Phương pháp:
Tạo lập hình lăng trụ đứng có chiều cao 15 cm, đáy là tam giác vuông có 3 cạnh là 5 cm, 12 cm, 13 cm:
- Vẽ 3 hình chữ nhật với kích thước 15 cm x 5 cm; 15 cm x 12 cm và 15 cm x 13 cm
- Gấp các cạnh BN và CP sao cho cạnh AM trùng với A’M’, đáy có một góc vuông, ta được hình lăng trụ đứng tam giác ABC.MNP
Lời giải:
Tạo lập hình lăng trụ đứng tam giác có đáy là tam giác vuông có độ dài hai cạnh góc vuông là 5 cm và 12 cm; chiều cao của hình lăng trụ đứng tam giác là 4 cm như sau:
- Vẽ ba hình chữ nhật và hai hình tam giác với kích thước như hình vẽ sau.
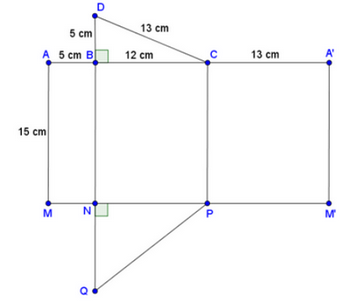
- Gấp các cạnh BN và CP sao cho cạnh AM trùng với A’M’.
- Gấp cạnh BC sao cho cạnh AB trùng với BD, cạnh CD trùng với CA’.
- Gấp cạnh NP sao cho cạnh MN trùng với NQ, cạnh PQ trùng với PM’.
Khi đó, ta được hình lăng trụ đứng tam giác ABC.MNP như Hình 6.
Bài 9 trang 67 SGK Toán 7 tập 1 - Chân trời sáng tạo
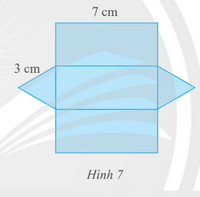
Người ta cắt một tấm bìa để tạo lập một lăng trụ đứng có đáy là tam giác đều với kích thước như Hình 7. Hãy cho biết độ dài các cạnh đáy và chiều cao của hình lăng trụ đứng.
Phương pháp:
Các cạnh không phải cạnh đáy thì là cạnh bên của lăng trụ đứng.
Độ dài cạnh bên của lăng trụ đứng là chiều cao.
Lời giải:
Hình lăng trụ đứng có đáy là tam giác đều nên độ dài tất cả các cạnh đáy bằng nhau và đều bằng 3 cm.
Chiều cao của hình lăng trụ đứng có đáy là tam giác đều là 7 cm.
Vậy hình lăng trụ đứng có đáy là tam giác đều có độ dài mỗi cạnh đáy đều bằng 3 cm và chiều cao là 7 cm.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài tập cuối chương 9 - CTST
- Bài 2. Làm quen với xác suất của biến cố ngẫu nhiên - CTST
- Bài 1. Làm quen với biến cố ngẫu nhiên - CTST
- Chương 9. Một số yếu tố xác suất - CTST
- Bài tập cuối chương 8 - CTST
- Bài 9. Tính chất ba đường phân giác của tam giác - CTST
- Bài 8. Tính chất ba đường cao của tam giác
- Bài 7. Tính chất ba đường trung tuyến của tam giác - CTST
- Bài 6. Tính chất ba đường trung trực của tam giác - CTST
- Bài 5. Đường trung trực của một đoạn thẳng - CTST
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!