Giải Toán 7 trang 79 Kết nối tri thức với cuộc sống tập 1

Bài 4.20 trang 79 SGK Toán 7 tập 1 - Kết nối tri thức

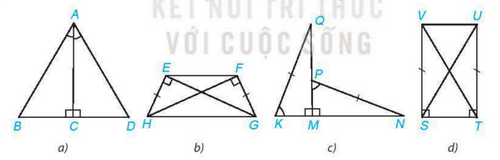
Mỗi hình sau có các cặp tam giác vuông nào bằng nhau? Vì sao?

Phương pháp:

Áp dụng các trường hợp bằng nhau của 2 tam giác vuông để chứng minh các cặp tam giác trên bằng nhau.

Lời giải:

a) Xét hai tam giác ACB vuông tại C và ACD vuông tại C có:

 (theo giả thiết).

AC chung.

Vậy  (góc nhọn – cạnh góc vuông).

b) Xét hai tam giác EGH vuông tại E và FHG vuông tại F có:

EH = FG (theo giả thiết).

HG chung.

Vậy  (cạnh huyền – cạnh góc vuông).

c) Xét hai tam giác QMK vuông tại M và NMP vuông tại M có:

QK = NP (theo giả thiết).

(theo giả thiết).

Vậy $\Delta QMK=\Delta NMP$ (cạnh huyền – góc nhọn).

d) Xét hai tam giác VST vuông tại S và UTS vuông tại T có:

VS = UT (theo giả thiết).

ST chung.

Vậy  (2 cạnh góc vuông).

Bài 4.21 trang 79 SGK Toán 7 tập 1 - Kết nối tri thức

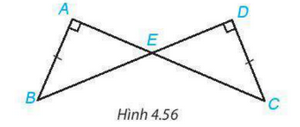
Cho hình 4.56, biết AB=CD, \(\widehat {BAC} = \widehat {BDC} = {90^o}\). Chứng minh rằng \(\Delta ABE = \Delta DCE\).

Phương pháp:

Chứng minh 2 tam giác vuông AEB và DEC bằng nhau theo trường hợp góc – cạnh - góc

Lời giải:

Vì tổng 3 góc trong 1 tam giác luôn bằng 180 độ.

Xét hai tam giác AED và DEC có:

\(\widehat {AEB} = \widehat {DEC}\)(đối đỉnh) và \(\widehat {BAC} = \widehat {BDC} = {90^o}\).

Suy ra: \(\widehat {AEB} = \widehat {DEC}\)

Xét 2 tam giác vuông AEB và DEC có:

AB=DC

\(\widehat {AEB} = \widehat {DEC}\)

=>\(\Delta AEB = \Delta DEC\)(g.c.g)

Bài 4.22 trang 79 SGK Toán 7 tập 1 - Kết nối tri thức

Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC.

Chứng minh rằng \(\Delta ABM = \Delta DCM\).

Phương pháp:

Chứng minh 2 tam giác bằng nhau theo trường hợp cạnh – góc - cạnh.

Lời giải:

Do ABCD là hình chữ nhật nên 

Hay 

Do đó tam giác ABM vuông tại B, tam giác DCM vuông tại C.

Do M là trung điểm của cạnh BC nên MB = MC.

Xét hai tam giác ABM vuông tại B và DCM vuông tại C có:

AB = CD (chứng minh trên).

MB = MC (chứng minh trên).

Vậy (2 cạnh góc vuông).

Sachbaitap.com