Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19 trang 57 SGK Toán 9 Chân trời sáng tạo tập 1

Bài 1 trang 57 SGK Toán 9 tập 1 - Chân trời sáng tạo

Biểu thức nào dưới đây có giá trị khác với các biểu thức còn lại?

A. \({\left( { - \sqrt 5 } \right)^2}\)

B. \(\sqrt {{5^2}} \)

C. \(\sqrt {{{\left( { - 5} \right)}^2}} \)

D. \( - {\left( {\sqrt 5 } \right)^2}\)

Phương pháp:

Dựa vào: Với số a không âm, ta có:

\({\left( {\sqrt a } \right)^2} = {\left( { - \sqrt a } \right)^2} = a\) và \(\sqrt {{a^2}}  = a\)

Lời giải:

Đáp án đúng là: D

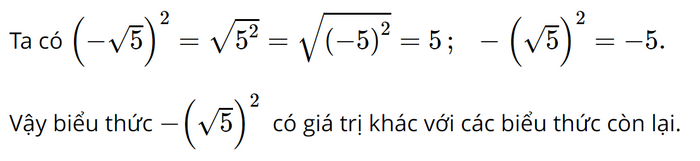
Bài 2 trang 57 SGK Toán 9 tập 1 - Chân trời sáng tạo

Có bao nhiêu số tự nhiên x để \(\sqrt {16 - x} \) là số nguyên?

A. 2

B. 3

C. 4

D. 5

Phương pháp:

Để \(\sqrt {16 - x} \) nguyên thì \(16 - x \ge 0\) và \(16 - x\) là số chính phương.

Tìm các số thỏa mãn điều kiện.

Lời giải:

Đáp án đúng ĐKXĐ: 16 – x ≥ 0 hay x ≤ 16.

Vì x là số tự nhiên nên 0 ≤ x ≤ 16.

Do đó 0 ≤ 16 – x ≤ 16.

Suy ra (16 – x) ∈ {0; 1; 4; 9; 16}.

Ta có bảng sau:

Vậy có 5 số tự nhiên x thỏa mãn yêu cầu là x ∈ {0; 7; 12; 15; 16}.

Bài 3 trang 57 SGK Toán 9 tập 1 - Chân trời sáng tạo

Giá trị của biểu thức \(\sqrt {16}  + \sqrt[3]{{ - 64}}\) bằng

A. 0

B. -2

C. 4

D. 5

Phương pháp:

Dựa vào: Với số a không âm, ta có:\(\sqrt {{a^2}}  = a\) và

Với số thực a ta có: \(\sqrt[3]{{{a^3}}} = a\)

Lời giải:

Đáp án đúng là: A

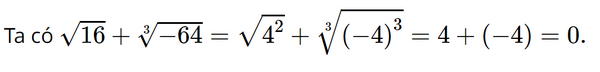
Bài 4 trang 57 SGK Toán 9 tập 1 - Chân trời sáng tạo

Đẳng thức nào sau đây không đúng?

A. \(\sqrt {16}  + \sqrt {144}  = 16\)

B. \(\sqrt {0,64} .\sqrt 9  = 2,4\)

C. \(\sqrt {{{( - 18)}^2}} :\sqrt {{6^2}}  = 3\)

D. \(\sqrt {{{( - 3)}^2}}  - \sqrt {{7^2}}  =  - 10\)

Phương pháp:

-  Xét vế trái dựa vào Với số a không âm, ta có:\(\sqrt {{a^2}}  = a\) và

Với số thực a ta có: \(\sqrt[3]{{{a^3}}} = a\)

-  Đưa thừa số ra ngoài dấu căn.

Lời giải:

Đáp án đúng là: D

Bài 5 trang 57 SGK Toán 9 tập 1 - Chân trời sáng tạo

Biết rằng \({\left( {2,6} \right)^2} = 6,76\), giá trị của biểu thức \(\sqrt {0,0676} \) bằng

A. 0,0026

B. 0,026

C. 0,26

D. 2,6

Phương pháp:

-  Dựa vào định nghĩa: Cho số thực a không âm. Số thực x thoả mãn x² = a được gọi là căn bậc hai của a.

-  Với số a không âm, ta có:\(\sqrt {{a^2}}  = a\)

Lời giải:

Đáp án đúng là: C

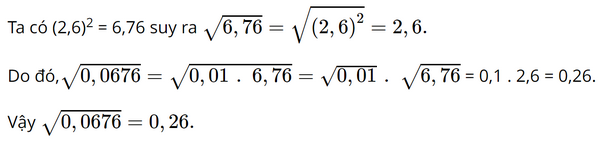
Bài 6 trang 57 SGK Toán 9 tập 1 - Chân trời sáng tạo

Rút gọn biểu thức \(\sqrt {9a}  - \sqrt {16a}  + \sqrt {64a} \) với \(a \ge 0\), ta có kết quả

A. \(15\sqrt a \)

B. 15a

C. \(7\sqrt a \)

D. 7a

Phương pháp:

Dựa vào: Với số a bất kì và b không âm, ta có:\(\sqrt {{a^2}b}  = \left| a \right|\sqrt b \)

Lời giải:

Đáp án đúng là: C

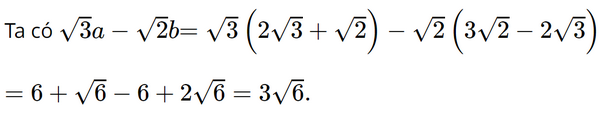
Bài 7 trang 57 SGK Toán 9 tập 1 - Chân trời sáng tạo

Cho a = \(2\sqrt 3  + \sqrt 2 \), b = \(3\sqrt 2  - 2\sqrt 3 \). Rút gọn biểu thức \(\sqrt 3 a - \sqrt 2 b\), ta có kết quả

A. \(3\sqrt 6 \)

B. \( - \sqrt 6 \)

C. \(6\sqrt 3 \)

D. \(12 - \sqrt 6 \)

Phương pháp:

Thay a và b vào biểu thức để tính.

Lời giải:

Đáp án đúng là: A

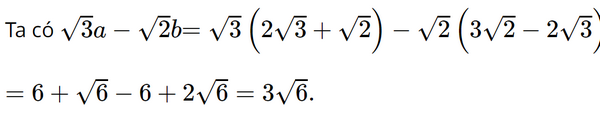
Bài 8 trang 57 SGK Toán 9 tập 1 - Chân trời sáng tạo

Trục căn thức ở mẫu biểu thức \(\frac{{\sqrt 6  - \sqrt 3 }}{{\sqrt 3 a}}\) với a > 0, ta có kết quả

A. \(\frac{{\sqrt 2  - 1}}{{\sqrt a }}\)

B. \(\frac{{\left( {\sqrt 6  - \sqrt 3 } \right)\sqrt a }}{{3a}}\)

C. \(\frac{{\left( {\sqrt 2  - 1} \right)\sqrt a }}{a}\)

D. \(\sqrt {2a}  - \sqrt a \)

Phương pháp:

Dựa vào trục căn thức ở mẫu: Với hai biểu thức A và B thoả mãn \(AB \ge 0,B \ne 0\)

\(\sqrt {\frac{A}{B}}  = \sqrt {\frac{{A.B}}{{{B^2}}}}  = \frac{{\sqrt {AB} }}{{\sqrt {{B^2}} }} = \frac{{\sqrt {AB} }}{{\left| B \right|}}\)

Lời giải:

Đáp án đúng là: A

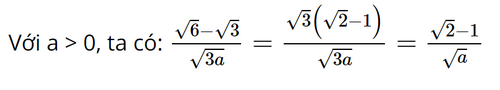
Bài 9 trang 57 SGK Toán 9 tập 1 - Chân trời sáng tạo

Kết quả của phép tính \(\sqrt {27} :\sqrt 6 .2\sqrt {18} \) là

A. 12

B. 18

C. 72

D. 144

Phương pháp:

Dựa vào: Với hai số thực a và b không âm, ta có:

\(\sqrt {a.b}  = \sqrt a .\sqrt b \)

Với số thực a không âm và số thực b dương, ta có:

\(\sqrt {\frac{a}{b}}  = \frac{{\sqrt a }}{{\sqrt b }}\)

Lời giải:

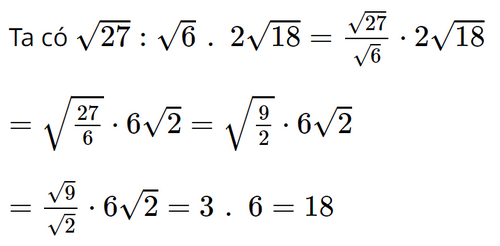
Bài 10 trang 57 SGK Toán 9 tập 1 - Chân trời sáng tạo

Rút gọn biểu thức \(\frac{1}{{2\sqrt a  + \sqrt 2 }} - \frac{1}{{2\sqrt a  - \sqrt 2 }}\) với \(a \ge 0\), \(a \ne \frac{1}{2}\), ta có kết quả

A. \(\frac{{\sqrt 2 }}{{1 - 2a}}\)

B. \(\frac{{\sqrt 2 }}{{2a - 1}}\)

C. \(\frac{{\sqrt a }}{{2a - 1}}\)

D. \(\frac{{\sqrt 2 }}{{1 - a}}\)

Phương pháp:

Quy đồng mẫu hai phân thức rồi tính

Lời giải:

Đáp án đúng là: D

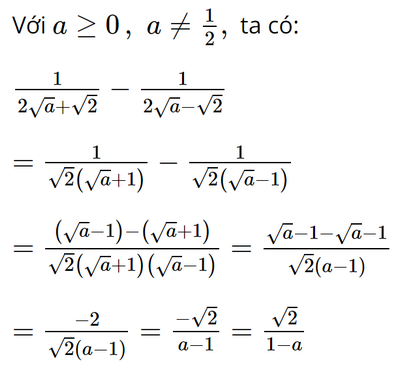
Bài 11 trang 58 SGK Toán 9 tập 1 - Chân trời sáng tạo

Tìm x, biết:

a) x² = 10

b) \(\sqrt x  = 8\)

c) x³ = - 0,027

d) \(\sqrt[3]{x} =  - \frac{2}{3}\)

Phương pháp:

-  Với a không âm. Số x thoả mãn x² = a. Mỗi số dương a có đúng hai căn bậc hai là: \(\sqrt a \) và - \(\sqrt a \).

-  Với số thực a không âm, ta có: \({\left( {\sqrt a } \right)^2} = a\).

-  Sử dụng phép khai căn bậc ba.

Lời giải:

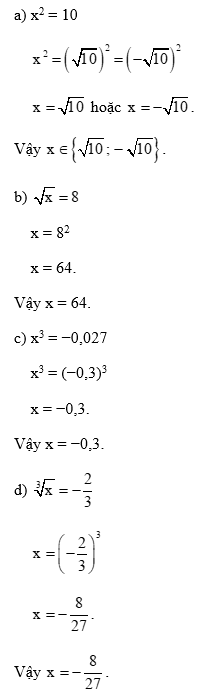
Bài 12 trang 58 SGK Toán 9 tập 1 - Chân trời sáng tạo

Biết rằng 1 < a < 5, rút gọn biểu thức

A = \(\sqrt {{{\left( {a - 1} \right)}^2}}  + \sqrt {{{\left( {a - 5} \right)}^2}} \).

Phương pháp:

Với số thực a không âm, ta có: \({\left( {\sqrt a } \right)^2} = \left| a \right|\).

Lời giải:

Vì 1 < a < 5 nên a – 1 > 0 và a – 5 < 0.

Khi đó |a – 1| = a – 1 và |a – 5| = 5 – a.

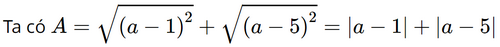
= a – 1 + 5 – a = 5.

Vậy với 1 < a < 5 thì A = 4.

Bài 13 trang 58 SGK Toán 9 tập 1 - Chân trời sáng tạo

Trục căn thức ở mẫu các biểu thức sau:

a) \(\frac{{4 - 2\sqrt 6 }}{{\sqrt {48} }}\)

b) \(\frac{{3 - \sqrt 5 }}{{3 + \sqrt 5 }}\)

c) \(\frac{a}{{a - \sqrt a }}\) với a > 0, a \( \ne \)1

Phương pháp:

Với hai biểu thức A và B thoả mãn A.B \( \ge \) 0, B \( \ne \)0, ta có:

\(\sqrt {\frac{A}{B}}  = \sqrt {\frac{{A.B}}{{{B^2}}}}  = \frac{{\sqrt {AB} }}{{\sqrt {{B^2}} }} = \frac{{\sqrt {AB} }}{{\left| B \right|}}\)

Lời giải:

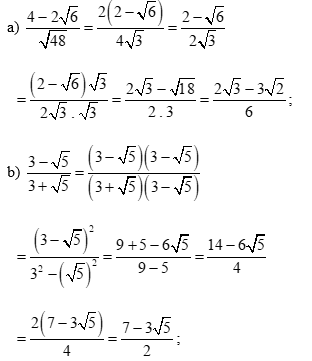
c) Với a > 0, a ≠ 1, ta có:

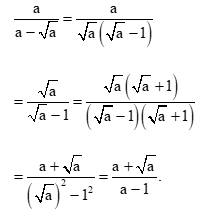
Bài 14 trang 58 SGK Toán 9 tập 1 - Chân trời sáng tạo

Biết rằng a > 0, b > 0 và ab = 16. Tính giá trị của biểu thức \(A = a\sqrt {\frac{{12b}}{a}}  + b\sqrt {\frac{{3a}}{b}} \).

Phương pháp:

Đưa thừa số vào trong căn làm xuất hiện tích ab rồi thay tích ab = 16 cho ở đề bài vào tính

Lời giải:

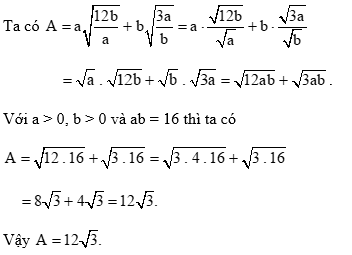
Bài 15 trang 58 SGK Toán 9 tập 1 - Chân trời sáng tạo

Tính \(\frac{{\sqrt 3  + \sqrt 2 }}{{\sqrt 3  - \sqrt 2 }} - \frac{{\sqrt 3  - \sqrt 2 }}{{\sqrt 3  + \sqrt 2 }}\).

Phương pháp:

Quy đồng mẫu thức rồi tính.

Lời giải:

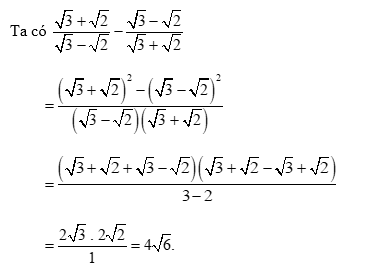
Bài 16 trang 58 SGK Toán 9 tập 1 - Chân trời sáng tạo

Một trục số được vẽ trên lưới ô vuông như Hình 1.

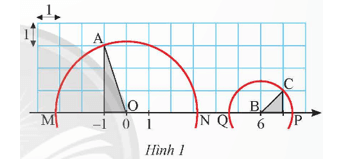
a) Đường tròn tâm O bán kính OA cắt trục số tại hai điểm M và N. Hai điểm M và N biểu diễn hai số thực nào?

b) Đường tròn tâm B bán kính BC cắt trục số tại hai điểm P và Q. Hai điểm P và Q biểu diễn hai số thực nào?

Phương pháp:

Tính bán kính mỗi đường tròn rồi suy ra các số thực mà các điểm biểu diễn.

Lời giải:

Bài 17 trang 58 SGK Toán 9 tập 1 - Chân trời sáng tạo

Cho hình hộp chữ nhật có chiều dài \(\sqrt {12} \)cm, chiều rộng\(\sqrt 8 \)cm, chiều cao \(\sqrt 6 \) như Hình 2.

a) Tính thể tích của hình hộp chữ nhật đó.

b) Tính diện tích xung quanh của hình hộp chữ nhật đó.

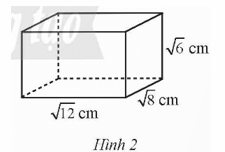
Phương pháp:

- Áp dụng công thức tính thể tích hình hộp chữ nhật = chiều dài.chiều rộng.chiều cao

- Áp dụng công thức tính diện tích xung quanh hình hộp chữ nhật = 2(chiều dài + chiều rộng) . chiều cao

Lời giải:

a) Thể tích của hình hộp chữ nhật đó là:

Bài 18 trang 58 SGK Toán 9 tập 1 - Chân trời sáng tạo

Rút gọn các biểu thức sau:

a) \(\left( {a\sqrt {\frac{3}{a}}  + 3\sqrt {\frac{a}{3}}  + \sqrt {12{a^3}} } \right):\sqrt 3 a\) với a > 0

b) \(\frac{{1 - a}}{{1 + \sqrt a }} + \frac{{1 - a\sqrt a }}{{1 - \sqrt a }}\) với \(a \ge 0;a \ne 1\)

Phương pháp:

-  Đưa thừa số vào trong căn rồi tính

-  Quy đồng mẫu thức rồi tính.

Lời giải:

a) Với a > 0, ta có:

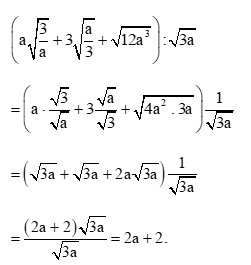
b) Với a ≥ 0, a ≠ 1, ta có:

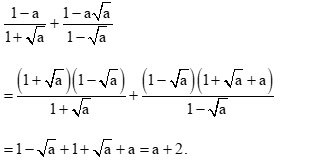
Bài 19 trang 58 SGK Toán 9 tập 1 - Chân trời sáng tạo

Cho biểu thức \(P = \left( {\frac{1}{{a + \sqrt a }} - \frac{1}{{\sqrt a  + 1}}} \right):\frac{{\sqrt a  - 1}}{{a + 2\sqrt a  + 1}}\) với a > 0 và a \( \ne \)1.

a) Rút gọn biểu thức P.

b) Tính giá trị của P khi a = 0,25

Phương pháp:

-  Quy đồng mẫu thức rồi tính.

-  Thay giá trị a vào biểu thức sau rút gọn để tính.

Lời giải:

a) Với a > 0, a ≠ 1, ta có:

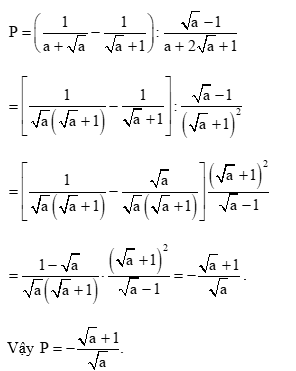
b) Khi a = 0,25 (TMĐK), ta có:

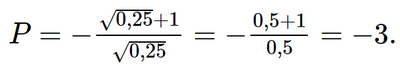
Vậy khi a = 0,25 thì P = −3.

Sachbaitap.com