Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9 trang 41 SGK Toán 9 Chân trời sáng tạo tập 1

Bài 1 trang 41 SGK Toán 9 tập 1 - Chân trời sáng tạo

Tìm các căn bậc hai của mỗi số sau:

a) 16

b) 2500

c) \(\frac{4}{{81}}\)

d) 0,09

Phương pháp:

Dựa vào VD1 trang 38 và làm tương tự.

Lời giải:

a) Ta có 4² = 16, nên 16 có hai căn bậc hai là 4 và −4.

b) Ta có 50² = 2 500, nên 2 500 có hai căn bậc hai là 50 và −50.

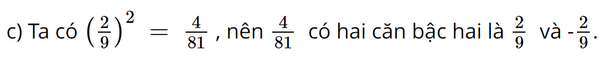
d) Ta có 0,3² = 0,09, nên 0,09 có hai căn bậc hai là 0,3 và −0,3.

Bài 2 trang 41 SGK Toán 9 tập 1 - Chân trời sáng tạo

Tính

a) \(\sqrt {100} \)

b) \(\sqrt {225} \)

c) \(\sqrt {2,25} \)

d) \(\sqrt {\frac{{16}}{{225}}} \)

Phương pháp:

Dựa vào VD3 trang 38 và làm tương tự.

Lời giải:

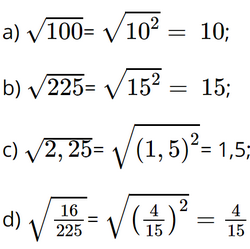
Bài 3 trang 41 SGK Toán 9 tập 1 - Chân trời sáng tạo

Biết rằng 25² = 625, tìm các căn bậc hai của các số 625 và 0,0625

Phương pháp:

Dựa vào VD1 trang 38 và làm tương tự.

Lời giải:

Vì 25² = 625 nên 625 có hai căn bậc hai là 25 và –25.

Khi đó, 0,0625 có hai căn bậc hai là 0,25 và –0,25.

Bài 4 trang 41 SGK Toán 9 tập 1 - Chân trời sáng tạo

Sử dụng máy tính cầm tay, tính (kết quả làm tròn đế chữ số thập phân thứ tư):

a) \(\sqrt {54} \)

b) \(\sqrt {24,68} \)

c) \(\sqrt 5  + \sqrt 6  + \sqrt 7 \)

Phương pháp:

Sử dụng máy tính cầm tay bỏ túi.

Lời giải:

Bài 5 trang 41 SGK Toán 9 tập 1 - Chân trời sáng tạo

Tính giá trị của các biểu thức:

a) \({\left( {\sqrt {5,25} } \right)^2} + {\left( { - \sqrt {1,75} } \right)^2}\)

b) \({\left( {\sqrt {102} } \right)^2} + \sqrt {{{98}^2}} \)

Phương pháp:

Dựa vào VD4 trang 38 và làm tương tự.

Lời giải:

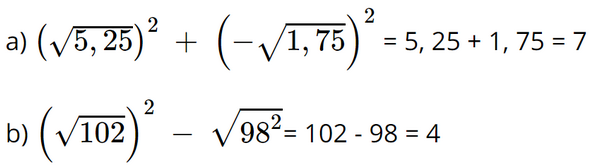
Bài 6 trang 41 SGK Toán 9 tập 1 - Chân trời sáng tạo

Tìm x, biết:

a) x² = 121

b) 4x² = 9

c) x² = 10

Phương pháp:

- Đưa vế phải về bình phương của một số

- Lấy căn bậc hai của cả hai vế để tìm x.

Lời giải:

a) x² = 121

x² = 11² = (−11)²

x = 11 hoặc x = −11.

Vậy x ∈ {−11; 11}.

b) 4x² = 9

Bài 7 trang 41 SGK Toán 9 tập 1 - Chân trời sáng tạo

Tính giá trị của các biểu thức sau khi x = 16; y = 9

a) \(\sqrt x  + \sqrt y \)

b) \(\sqrt {x + y} \)

c) \(\frac{1}{2}\sqrt {xy} \)

d) \(\frac{1}{6}x\sqrt y \)

Phương pháp:

Thay giá trị x và y vào từng biểu thức để tính.

Lời giải:

Bài 8 trang 41 SGK Toán 9 tập 1 - Chân trời sáng tạo

Cho biểu thức P = \(\sqrt {{x^2} - xy + 1} \). Tính giá trị của P khi:

a) x = 3; y = - 2

b) x = 1; y = 4

Phương pháp:

Thay giá trị x và y vào từng biểu thức để tính.

Lời giải:

a) Thay x = 3, y = −2 vào biểu thức P, ta có:

Vậy khi x = 16, y = 9 giá trị của các biểu thức bằng 5.

Bài 9 trang 41 SGK Toán 9 tập 1 - Chân trời sáng tạo

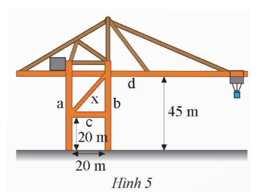
Trên cần trục ở Hình 5, hai trụ a và b đứng cách nhau 20 m, hai xà ngang c và d lần lượt có độ cao 20 m và 45 m so với mặt đất. Xà chéo x có độ dài bao nhiêu mét (kết quả làm tròn đến hàng đơn vị)?

Phương pháp:

Dựa vào định lí Pythagore trong tam giác vuông để tìm xà chéo x.

Lời giải:

Gọi các điểm A, B, C, D, E như trên hình vẽ.

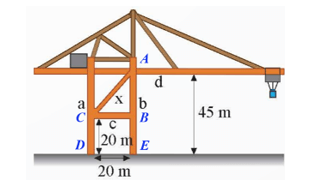
Vì hai trụ a và b đứng cách nhau 20 m nên DE = BC = 20 m.

Vì xà ngang d có độ cao 45 m so với mặt đất nên AE = 45 m.

Suy ra AB = AE – BE = 45 – 20 = 25 (m).

Áp dụng định lí Pythagore vào tam giác ABC vuông tại B, ta có:

AC² = AB² + BC² = 25² + 20² = 1025.

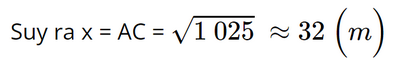
Vậy xà chéo x có độ dài khoảng 32 mét (làm tròn đến hàng đơn vị).

Sachbaitap.com