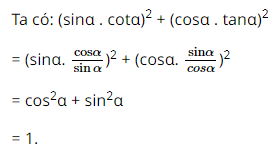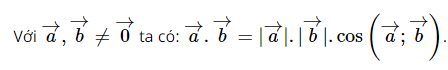Giải SBT Toán 10 trang 106, 107, 108 Cánh Diều tập 1
Giải bài 67, 68, 69, 70, 71 trang 106, bài 72, 73, 74, 75, 76, 77, 78 trang 107, bài 79, 80, 81, 82 trang 108 SBT Toán 10 Cánh Diều tập 1. Bài 77. Một người quan sát đứng ở bờ sông muốn đo độ rộng của khúc sông chỗ chảy qua vị trí đang đứng.
Xem thêm: Bài tập cuối chương IV
Bài 67 trang 106 SBT Toán 10 - Cánh Diều
Cho góc nhọn \(\alpha \). Biểu thức (sin\(\alpha \). cot\(\alpha \))2 + (cos\(\alpha \) . tan\(\alpha \))2 bằng:
A. 2
B. tan²\(\alpha \) + cot²\(\alpha \)
C. 1
D. sin\(\alpha \) + cos\(\alpha \)
Phương pháp:
Sử dụng các công thức lượng giác cơ bản để biến đổi giả thiết
Lời giải:
Đáp án đúng là C
Bài 68 trang 106 SBT Toán 10 - Cánh Diều
Cho các vectơ \(\overrightarrow a ,\overrightarrow b \ne \overrightarrow 0 \). Phát biểu nào sau đây là đúng?
A. \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\left| {\cos \left( {\overrightarrow a ,\overrightarrow b } \right)} \right|\)
B. \(\left| {\overrightarrow a .\overrightarrow b } \right| = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)
C. \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\sin \left( {\overrightarrow a ,\overrightarrow b } \right)\)
D. \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)
Phương pháp:
Sử dụng định nghĩa tích vô hướng của hai vectơ
Lời giải:
Đáp án đúng là D
Bài 69 trang 106 SBT Toán 10 - Cánh Diều
Cho tứ giác ABCD. Biểu thức \(\overrightarrow {AB} .\overrightarrow {CD} + \overrightarrow {BC} .\overrightarrow {CD} + \overrightarrow {CA} .\overrightarrow {CD} \) bằng:
A. CD²
B. 0
C. \(\overrightarrow 0 \)
D. 1
Phương pháp:
Bước 1: Đặt \(\overrightarrow {CD} \) là nhân tử chung
Bước 2: Sử dụng các quy tắc vectơ và định nghĩa tích vô hướng của hai vectơ để biến đổi giả thiết
Lời giải:
Đáp án đúng là B
Bài 70 trang 106 SBT Toán 10 - Cánh Diều
Cho góc nhọn \(\alpha \). Biểu thức tan\(\alpha \). tan(90° - \(\alpha \)) bằng:
A. tan\(\alpha \) + cot\(\alpha \)
B. tan²\(\alpha \)
C. 1
D. tan²\(\alpha \) + cot²\(\alpha \)
Phương pháp:
Sử dụng định lí giá trị lượng giác của hai góc phụ nhau và các công thức lượng giác cơ bản để biến đổi giả thiết
Lời giải:
Đáp án đúng là C
Bài 71 trang 106 SBT Toán 10 - Cánh Diều
Cho \(\alpha \) thoả mãn \(\sin \alpha = \frac{3}{5}\). Tính cos\(\alpha \), tan\(\alpha \), cot\(\alpha \), sin(90° - \(\alpha \)), cos(90° - \(\alpha \)), sin(180° – \(\alpha \)),
cos(180° – \(\alpha \)) trong các trường hợp sau:
a) 0° < \(\alpha \) < 90°
b) 90° < \(\alpha \) < 180°
Lời giải:
a) Theo giả thiết, 0° < \(\alpha \) < 90° \( \Rightarrow \cos \alpha > 0,\tan \alpha > 0,\cot \alpha > 0\)
+ Ta có: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Rightarrow {\cos ^2}\alpha = 1 - {\sin ^2}\alpha = 1 - {\left( {\frac{3}{5}} \right)^2} = \frac{{16}}{{25}}\) \( \Rightarrow \cos \alpha = \frac{4}{5}\)
+ \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{3}{4};\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{4}{3}\)
+ \(\sin ({90^0} - \alpha ) = \cos \alpha = \frac{4}{5};\cos ({90^0} - \alpha ) = \sin \alpha = \frac{3}{5}\)
+ \(\sin \left( {{{180}^0} - \alpha } \right) = \sin \alpha = \frac{3}{5};\cos \left( {{{180}^0} - \alpha } \right) = - \cos \alpha = - \frac{4}{5}\)
b) Theo giả thiết, 90° < \(\alpha \) < 180° \( \Rightarrow \cos \alpha < 0,\tan \alpha < 0,\cot \alpha < 0\)
+ Ta có: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Rightarrow {\cos ^2}\alpha = 1 - {\sin ^2}\alpha = 1 - {\left( {\frac{3}{5}} \right)^2} = \frac{{16}}{{25}}\) \( \Rightarrow \cos \alpha = - \frac{4}{5}\)
+ \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = - \frac{3}{4};\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = - \frac{4}{3}\)
+ \(\sin ({90^0} - \alpha ) = \cos \alpha = - \frac{4}{5};\cos ({90^0} - \alpha ) = \sin \alpha = \frac{3}{5}\)
+ \(\sin \left( {{{180}^0} - \alpha } \right) = \sin \alpha = \frac{3}{5};\cos \left( {{{180}^0} - \alpha } \right) = - \cos \alpha = \frac{4}{5}\)
Bài 72 trang 107 SBT Toán 10 - Cánh Diều
Cho tam giác ABC có AB = 4, AC = 6, \(\widehat {BAC}\) = 60°. Tính (làm tròn kết quả đến hàng đơn vị):
a) Độ dài cạnh BC và độ lớn góc B
b) Bán kính đường tròn ngoại tiếp R
c) Diện tích của tam giác ABC
d) Độ dài đường cao xuất phát tử A
e) \(\overrightarrow {AB.} \overrightarrow {AC} ,\overrightarrow {AM} .\overrightarrow {AC} \) với M là trung điểm của BC
Lời giải:
a) Áp dụng định lí cosin cho ∆ABC ta có:
+ \(B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\)\( = {4^2} + {6^2} - 2.4.6.\cos {60^0} = 28\) \( \Rightarrow BC = 2\sqrt 7 \)
+ \(\cos B = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}} \Rightarrow \widehat B \approx {79^0}\)
b) Áp dụng định lí sin cho ∆ABC ta có: \(\frac{{BC}}{{\sin A}} = 2R \Rightarrow R = \frac{{BC}}{{2\sin A}} = \frac{5}{{2.\sin {{60}^0}}} \approx 3\)
c) Diện tích tam giác ABC là: \({S_{ABC}} = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}.4.6.\sin {60^0} \approx 10\)
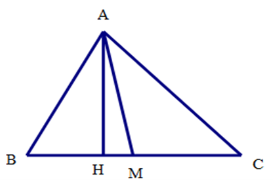
d) Gọi AH là một đường cao của tam giác ABC
Ta có: \({S_{ABC}} = \frac{1}{2}AH.BC \Rightarrow AH = \frac{{2{S_{ABC}}}}{{BC}} \approx 4\)
e) Ta có:
+\(\overrightarrow {AB.} \overrightarrow {AC} = AB.AC.\cos \widehat {BAC} = 4.6.\cos {60^0} = 12\)
+ Do M là trung điểm BC nên \(\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)
\(\overrightarrow {AM} .\overrightarrow {AC} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\overrightarrow {AC} = \frac{1}{2}\overrightarrow {AB} .\overrightarrow {AC} + \frac{1}{2}{\overrightarrow {AC} ^2} = \frac{1}{2}.12 + \frac{1}{2}{.6^2} = 24\)
Bài 73 trang 107 SBT Toán 10 - Cánh Diều
Cho tam giác ABC. Chứng minh rằng \(\overrightarrow {AB} .\overrightarrow {AC} = \frac{1}{2}\left( {A{B^2} + A{C^2} - B{C^2}} \right)\) (*)
Lời giải:
Xét \(A{B^2} + A{C^2} - B{C^2} = \left( {{{\overrightarrow {AB} }^2} + {{\overrightarrow {AC} }^2} - {{\overrightarrow {BC} }^2}} \right) = \left[ {{{\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)}^2} - 2\overrightarrow {AB} .\overrightarrow {AC} - {{\overrightarrow {BC} }^2}} \right]\)
\( = \left[ {\left( {\overrightarrow {AB} + \overrightarrow {AC} - \overrightarrow {BC} } \right)\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {BC} } \right) - 2\overrightarrow {AB} .\overrightarrow {AC} } \right]\) \( = \left[ {\left( {\overrightarrow {AB} + \overrightarrow {CB} - \overrightarrow {CA} } \right)\left( {\overrightarrow {AC} + \overrightarrow {AC} } \right) - 2\overrightarrow {AB} .\overrightarrow {AC} } \right]\)
\( = \left( {2\overrightarrow {AB} .2\overrightarrow {AC} - 2\overrightarrow {AB} .\overrightarrow {AC} } \right) = 2\overrightarrow {AB} .\overrightarrow {AC} \)
Vậy \(\overrightarrow {AB} .\overrightarrow {AC} = \frac{1}{2}\left( {A{B^2} + A{C^2} - B{C^2}} \right)\) (ĐPCM)
Bài 74 trang 107 SBT Toán 10 - Cánh Diều
Cho tam giác ABC có AB = 5, BC = 6, CA = 7. Tính:
a) sin\(\widehat {ABC}\)
b) Diện tích tam giác ABC
c) Độ dài trung tuyến AM
Lời giải:
a) Ta có: \(\cos \widehat {ABC} = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2AB.BC}} = \frac{1}{5}\)
Mặt khác, \({\sin ^2}\widehat {ABC} + {\cos ^2}\widehat {ABC} = 1 \Rightarrow {\sin ^2}\widehat {ABC} = \frac{{24}}{{25}}\) \( \Rightarrow \sin \widehat {ABC} = \frac{{2\sqrt 6 }}{5}\) (Do \({0^0} < \widehat {ABC} < {180^0}\))
b) Diện tích ∆ABC là: \(S = \frac{1}{2}AB.BC.\sin \widehat {ABC} = \frac{1}{2}.5.6.\frac{{2\sqrt 6 }}{5} = 6\sqrt 6 \)
c) Gọi AM là một đường trung tuyến của ∆ABC, ta có:
\(A{M^2} = \frac{{A{B^2} + A{C^2}}}{2} - \frac{{B{C^2}}}{4} = 28\) \( \Rightarrow AM = 2\sqrt 7 \)
Bài 75 trang 107 SBT Toán 10 - Cánh Diều
Cho ba điểm phân biệt I, A, B và số thực k ≠ 1 thoả mãn \(\overrightarrow {IA} = k\overrightarrow {IB} \). Chứng minh rằng với O là điểm bất kì ta có:
\(\overrightarrow {OI} = \left( {\frac{1}{{1 - k}}} \right)\overrightarrow {OA} - \left( {\frac{k}{{1 - k}}} \right)\overrightarrow {OB} \) (*)
Lời giải:
Theo giả thiết, \(\overrightarrow {IA} = k\overrightarrow {IB} \)
Xét vế phải (*) ta có:
VT = \(\left( {\frac{1}{{1 - k}}} \right)\overrightarrow {OA} - \left( {\frac{k}{{1 - k}}} \right)\overrightarrow {OB} = \left( {\frac{1}{{1 - k}}} \right)\left( {\overrightarrow {OI} + \overrightarrow {IA} } \right) - \left( {\frac{k}{{1 - k}}} \right)\left( {\overrightarrow {OI} + \overrightarrow {IB} } \right)\)
\( = \left( {\frac{1}{{1 - k}}} \right)\overrightarrow {OI} + \left( {\frac{1}{{1 - k}}} \right)\overrightarrow {IA} - \left( {\frac{k}{{1 - k}}} \right)\overrightarrow {OI} - \left( {\frac{k}{{1 - k}}} \right)\overrightarrow {IB} \) \( = \left( {\frac{1}{{1 - k}} - \frac{k}{{1 - k}}} \right)\overrightarrow {OI} + \left( {\frac{1}{{1 - k}}} \right).k\overrightarrow {IB} - \left( {\frac{k}{{1 - k}}} \right)\overrightarrow {IB} \)
\( = \overrightarrow {OI} + \left( {\frac{1}{{1 - k}}} \right).k\overrightarrow {IB} - \left( {\frac{k}{{1 - k}}} \right)\overrightarrow {IB} = \overrightarrow {OI} + \left( {\frac{k}{{1 - k}} - \frac{k}{{1 - k}}} \right)\overrightarrow {IB} \) \( = \overrightarrow {OI} \) (ĐPCM)
Bài 76 trang 107 SBT Toán 10 - Cánh Diều
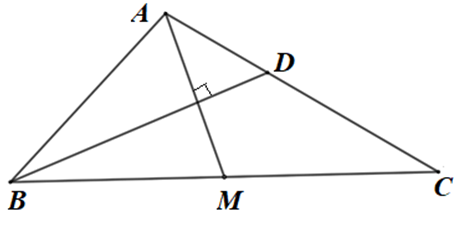
Cho tam giác ABC có AB = 4, AC = 5, \(\widehat {BAC}\) = 120°. Điểm M là trung điểm của đoạn thẳng BC, điểm D thoả mãn \(\overrightarrow {AD} = \frac{2}{5}\overrightarrow {AC} \). Tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AC} \) và chứng minh \(AM \bot BD\)
Lời giải:
a) Ta có: \(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos \widehat {BAC} = 4.5.\cos {120^0} = - 10\)
b) Do M là trung điểm BC nên \(\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\); \(AD = \frac{2}{5}AC = 2\)
Xét \(\overrightarrow {AM} .\overrightarrow {BD} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\left( {\overrightarrow {AD} - \overrightarrow {AB} } \right)\)\( = \frac{1}{2}\overrightarrow {AB} .\overrightarrow {AD} - \frac{1}{2}{\overrightarrow {AB} ^2} + \frac{1}{2}\overrightarrow {AC} .\overrightarrow {AD} - \frac{1}{2}\overrightarrow {AC} .\overrightarrow {AB} \)
\( = \frac{1}{2}AB.AD.\cos \widehat {BAD} - \frac{1}{2}A{B^2} + \frac{1}{2}.\frac{2}{5}A{C^2} - \frac{1}{2}\overrightarrow {AB} .\overrightarrow {AC} \)
\( = \frac{1}{2}.4.2.\cos {120^0} - \frac{1}{2}{.4^2} + \frac{1}{5}{.5^2} - \frac{1}{2}.( - 10) = 0\)
\( \Rightarrow \overrightarrow {AM} .\overrightarrow {BD} = 0 \Rightarrow AM \bot BD\)
Bài 77 trang 107 SBT Toán 10 - Cánh Diều
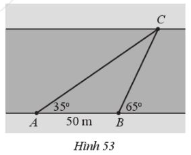
Một người quan sát đứng ở bờ sông muốn đo độ rộng của khúc sông chỗ chảy qua vị trí đang đứng (khúc sông tương đối thẳng, có thể xem hai bờ song song với nhau).
Từ vị trí đang đứng A, người đó đo được góc nghiêng \(\alpha \) = 35° so với bờ sông tới một vị trí C quan sát được ở phía bờ bên kia. Sau đó di chuyển dọc bờ sông đến vị trí B cách A một khoảng d = 50 m và tiếp tục đo được góc nghiêng \(\beta \)=65° so với bờ sông tới vị trí C đã chọn (Hình 53). Hỏi độ rộng của con sông chỗ chảy qua vị trí người quan sát đang đứng là bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?
Lời giải:
Ta có: \(\widehat {ABC} = {180^0} - {65^0} = {115^0} \Rightarrow \widehat {ACB} = {180^0} - \left( {\widehat {CAB} + \widehat {ABC}} \right) = {30^0}\)
Áp dụng định lí sin cho ∆ABC ta có: \(\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}} \Rightarrow BC = \frac{{AB.\sin A}}{{\sin C}} = \frac{{50.\sin {{35}^0}}}{{\sin {{30}^0}}} \approx 57,36\) (m)
Diện tích tam giác ABC là: \(S = \frac{1}{2}BC.AB.\sin \widehat {ABC} = \frac{1}{2}.57,36.50.\sin {115^0} \approx 1299,65\) (m2)
Gọi hc là chiều cao kẻ từ đỉnh C của ∆ABC
Ta có: \(S = \frac{1}{2}AB.{h_C} \Rightarrow {h_C} = \frac{{2S}}{{AB}} \approx 51,99\) (m)
Vậy chiều rộng khúc sông là 51,99 m
Bài 78 trang 107 SBT Toán 10 - Cánh Diều
Cho hai vectơ \(\overrightarrow a ,\overrightarrow b \) và \(\left| {\overrightarrow a } \right| = 4,\left| {\overrightarrow b } \right| = 5,\left( {\overrightarrow a ,\overrightarrow b } \right) = {135^0}\). Tính \(\left( {\overrightarrow a + 2\overrightarrow b } \right).\left( {2\overrightarrow a - \overrightarrow b } \right)\)
Phương pháp:
Rút gọn biểu thức \(\left( {\overrightarrow a + 2\overrightarrow b } \right).\left( {2\overrightarrow a - \overrightarrow b } \right)\) rồi sử dụng định nghĩa tích vô hướng của hai vectơ
Lời giải:
Ta có: \(\left( {\overrightarrow a + 2\overrightarrow b } \right).\left( {2\overrightarrow a - \overrightarrow b } \right) = 2{\overrightarrow a ^2} - \overrightarrow a .\overrightarrow b + 4\overrightarrow a .\overrightarrow b - 2{\overrightarrow b ^2} = 2{\left| {\overrightarrow a } \right|^2} + 3\overrightarrow a .\overrightarrow b - 2{\left| {\overrightarrow b } \right|^2}\)
Xét \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = 4.5.\cos {135^0} = - 10\sqrt 2 \)
\( \Rightarrow \left( {\overrightarrow a + 2\overrightarrow b } \right).\left( {2\overrightarrow a - \overrightarrow b } \right) = {2.4^2} + 3.\left( { - 10\sqrt 2 } \right) - {2.5^2} = - 18 - 30\sqrt 2 \)
Bài 79 trang 108 SBT Toán 10 - Cánh Diều
a) Chứng minh đẳng thức \({\left| {\overrightarrow a + \overrightarrow b } \right|^2} = {\left| {\overrightarrow a } \right|^2} + {\left| {\overrightarrow b } \right|^2} + 2\overrightarrow a .\overrightarrow b \) với \(\overrightarrow a ,\overrightarrow b \) là hai vectơ bất kì
b) Cho \(\left| {\overrightarrow a } \right| = 2,\left| {\overrightarrow b } \right| = 3,\left| {\overrightarrow a + \overrightarrow b } \right| = \sqrt 7 \). Tinh \(\overrightarrow a .\overrightarrow b \) và \(\left( {\overrightarrow a ,\overrightarrow b } \right)\)
Phương pháp:
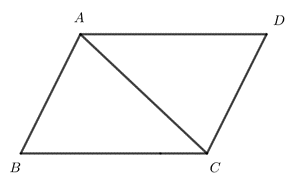
Bước 1: Dựng hình bình hành ABCD sao cho \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AD} = \overrightarrow b \)
Bước 2: Sử dụng các quy tắc vectơ và hệ thức lượng trong tam giác để chứng minh đẳng thức
\({\left| {\overrightarrow a + \overrightarrow b } \right|^2} = {\left| {\overrightarrow a } \right|^2} + {\left| {\overrightarrow b } \right|^2} + 2\overrightarrow a .\overrightarrow b \)
Bước 3: Áp dụng đẳng thức \({\left| {\overrightarrow a + \overrightarrow b } \right|^2} = {\left| {\overrightarrow a } \right|^2} + {\left| {\overrightarrow b } \right|^2} + 2\overrightarrow a .\overrightarrow b \) để tính \(\overrightarrow a .\overrightarrow b \) và \(\left( {\overrightarrow a ,\overrightarrow b } \right)\)
Lời giải:
a) Xét hình bình hành ABCD thỏa mãn \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AD} = \overrightarrow b \)
Theo quy tắc hình bình hành ta có:
\(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \Rightarrow \left| {\overrightarrow a + \overrightarrow b } \right| = AC\)
Mà \(A{C^2} = A{B^2} + B{C^2} - 2AB.AC.\cos B = A{B^2} + A{D^2} - 2AB.AD.\cos B\)
Mặt khác, \(\widehat {BAD} + \widehat B = {180^0} \Rightarrow \cos \widehat B = - \cos \widehat {BAD}\)
\( \Rightarrow A{C^2} = A{B^2} + A{D^2} + 2AB.AD.\cos \widehat {BAD} = {\left| {\overrightarrow {AB} } \right|^2} + {\left| {\overrightarrow {AD} } \right|^2} + 2AB.AD.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = {\left| {\overrightarrow {AB} } \right|^2} + {\left| {\overrightarrow {AD} } \right|^2} + 2\overrightarrow {AB} .\overrightarrow {AD} \)
\( \Rightarrow {\left| {\overrightarrow a + \overrightarrow b } \right|^2} = {\left| {\overrightarrow a } \right|^2} + {\left| {\overrightarrow b } \right|^2} + 2\overrightarrow a .\overrightarrow b \) (ĐPCM)
b) Theo a) \({\left| {\overrightarrow a + \overrightarrow b } \right|^2} = {\left| {\overrightarrow a } \right|^2} + {\left| {\overrightarrow b } \right|^2} + 2\overrightarrow a .\overrightarrow b \)
\( \Rightarrow \overrightarrow a .\overrightarrow b = \frac{{{{\left| {\overrightarrow a + \overrightarrow b } \right|}^2} - {{\left| {\overrightarrow a } \right|}^2} - {{\left| {\overrightarrow b } \right|}^2}}}{2} = \frac{{{{\sqrt 7 }^2} - {2^2} - {3^2}}}{2} = - 3\)
Ta có: \(\overrightarrow a .\overrightarrow b = - 3 \Leftrightarrow \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = - 3 \Leftrightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{ - 3}}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = - \frac{1}{2}\) \( \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {120^0}\)
Bài 80 trang 108 SBT Toán 10 - Cánh Diều
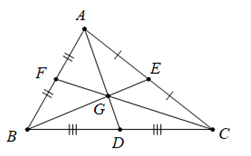
Cho tam giác ABC có ba trung tuyến AD, BE, CF. Chứng minh rằng:
\(\overrightarrow {AD} .\overrightarrow {BC} + \overrightarrow {BE} .\overrightarrow {CA} + \overrightarrow {CF} .\overrightarrow {AB} = 0\)(*)
Phương pháp:
Sử dụng tính chất trung điểm của đoạn thẳng để biến đổi vế trái đẳng thức (*)
Lời giải:
+ Do D là trung điểm BC nên \(\overrightarrow {AD} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)
+ Do E là trung điểm AC nên \(\overrightarrow {BE} = \frac{1}{2}\left( {\overrightarrow {BA} + \overrightarrow {BC} } \right)\)
+ Do F là trung điểm AB nên \(\overrightarrow {CF} = \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {CB} } \right)\)
Ta có: \(\overrightarrow {AD} .\overrightarrow {BC} + \overrightarrow {BE} .\overrightarrow {CA} + \overrightarrow {CF} .\overrightarrow {AB} \)\( = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\overrightarrow {BC} + \frac{1}{2}\left( {\overrightarrow {BA} + \overrightarrow {BC} } \right).\overrightarrow {CA} + \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {CB} } \right).\overrightarrow {AB} \)
\( = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {AC} .\overrightarrow {BC} + \overrightarrow {BA} .\overrightarrow {CA} + \overrightarrow {BC} .\overrightarrow {CA} + \overrightarrow {CA} .\overrightarrow {AB} + \overrightarrow {CB} .\overrightarrow {AB} } \right)\)
\( = \frac{1}{2}\left( { - \overrightarrow {BA} .\overrightarrow {BC} + \overrightarrow {CA} .\overrightarrow {CB} + \overrightarrow {AB} .\overrightarrow {AC} - \overrightarrow {CB} .\overrightarrow {CA} - \overrightarrow {AC} .\overrightarrow {AB} + \overrightarrow {BC} .\overrightarrow {BA} } \right)\)\( = \frac{1}{2}.0 = 0\) (ĐPCM)
Bài 81 trang 108 SBT Toán 10 - Cánh Diều
Cho tử giác ABCD. M là điểm thay đổi trong mặt phẳng thoả mãn \(\left( {\overrightarrow {MA} + \overrightarrow {MB} } \right).\left( {\overrightarrow {MC} + \overrightarrow {MD} } \right) = 0\). Chứng minh rằng điểm M luôn nằm trên một đường tròn cố định.
Lời giải:
Theo giả thiết, \(\left( {\overrightarrow {MA} + \overrightarrow {MB} } \right).\left( {\overrightarrow {MC} + \overrightarrow {MD} } \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}\overrightarrow {MA} + \overrightarrow {MB} = 0\\\overrightarrow {MC} + \overrightarrow {MD} = 0\end{array} \right.\)
Gọi P, Q lần lượt là trung điểm của AB và CD \( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MP} \\\overrightarrow {MC} + \overrightarrow {MD} = 2\overrightarrow {MQ} \end{array} \right.\)
\( \Rightarrow \left( {\overrightarrow {MA} + \overrightarrow {MB} } \right).\left( {\overrightarrow {MC} + \overrightarrow {MD} } \right) = 0 \Leftrightarrow 2\overrightarrow {MP} .2\overrightarrow {MQ} = 0 \Leftrightarrow \overrightarrow {MP} .\overrightarrow {MQ} = 0\)
+ Nếu M không trùng với P hoặc Q thì \(\overrightarrow {MP} .\overrightarrow {MQ} = 0 \Leftrightarrow MP \bot MQ\)
\( \Rightarrow \) Tập hợp các điểm M là đường tròn đường kính PQ
+ Nếu M trùng với P hoặc Q thì hiển nhiên M thuộc đường tròn đường kính PQ
Vậy M luôn thuộc đường tròn đường kính PQ cố định
Bài 82 trang 108 SBT Toán 10 - Cánh Diều
Cho tam giác ABC và đường thẳng d không có điểm chung với bất kì cạnh nào của tam giác. M là điểm thay đổi trên đường thẳng d. Xác định vị trí của M sao cho biểu thức \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right|\) đạt giá trị nhỏ nhất.
Lời giải:
Gọi G là trọng tâm tam giác ABC. Khi đó \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
Ta có: \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = \left| {\overrightarrow {MG} + \overrightarrow {GA} + \overrightarrow {MG} + \overrightarrow {GB} + \overrightarrow {MG} + \overrightarrow {GC} } \right|\)
\( = \left| {3\overrightarrow {MG} + \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right)} \right| = 3\left| {\overrightarrow {MG} } \right|\)\( \ge 3HG\) (với H là hình chiếu của G trên d)
Vậy với M là hình chiếu của G trên đường thẳng d thì biểu thức \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right|\) đạt giá trị nhỏ nhất
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài tập cuối chương VII
- Bài 6. Ba đường conic
- Bài 5. Phương trình đường tròn
- Bài 4. Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng
- Bài 3. Phương trình đường thẳng
- Bài 2. Biểu thức tọa độ của các phép toán vectơ
- Bài 1. Tọa độ của vectơ
- Chương VII. Phương pháp tọa độ trong mặt phẳng
- Bài tập cuối chương VI
- Bài 5. Xác suất của biến cố
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!