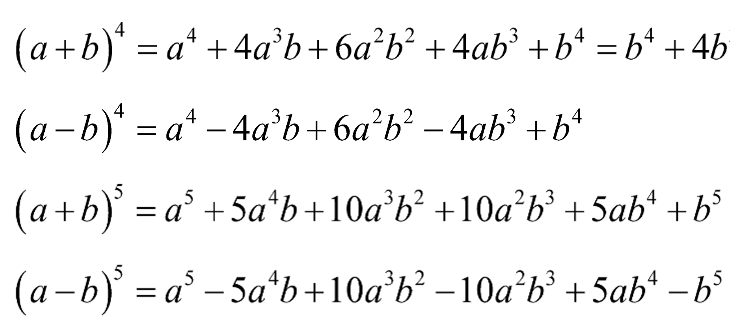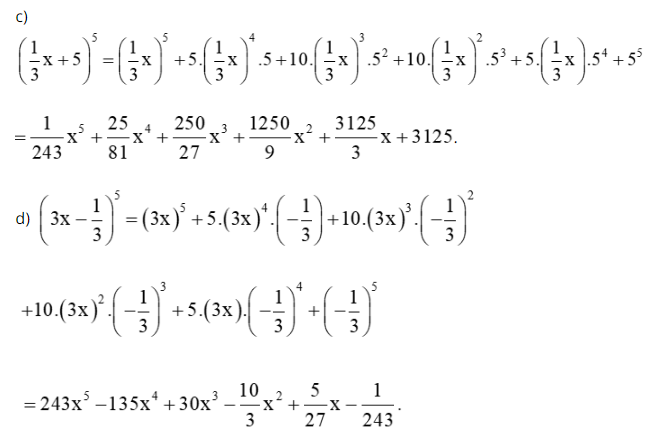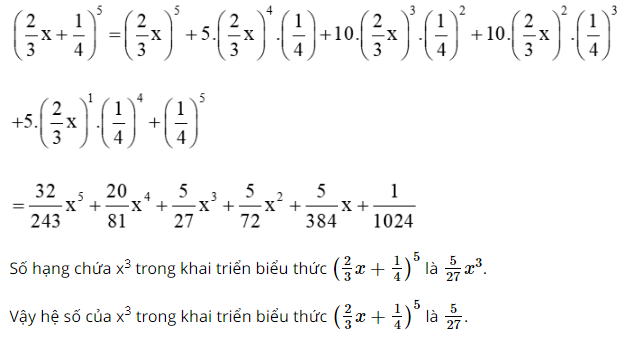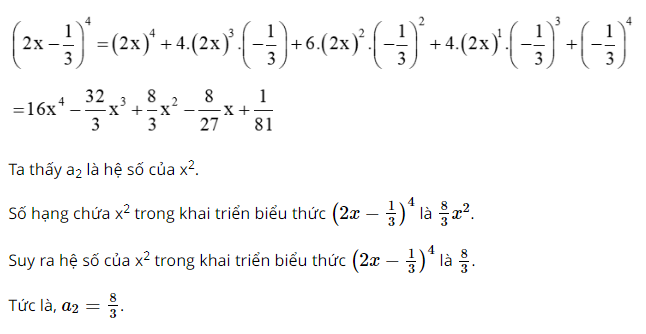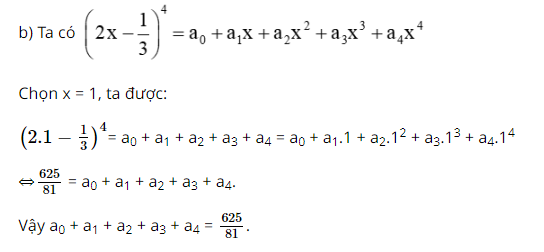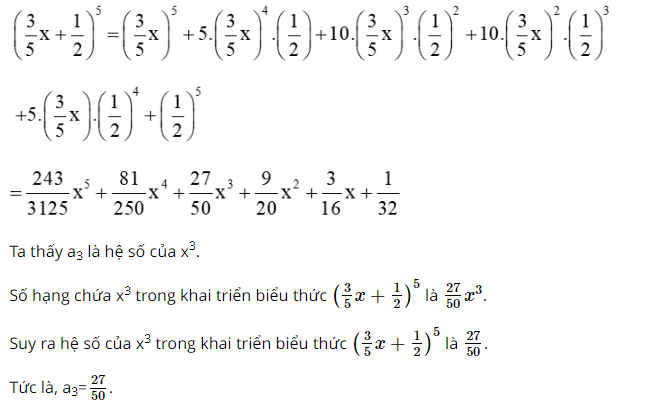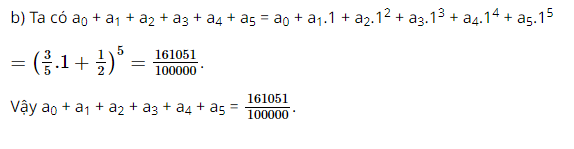Giải SBT Toán 10 trang 15, 16 Cánh Diều tập 2
Giải bài 28 trang 15, bài 29, 30, 31, 32, 33, 34, 35, 36, 37 trang 16 SBT Toán 10 Cánh Diều tập 2 - Bài 37. Tính các tổng sau (Không sử dụng máy tính cầm tay):
Bài 28 trang 15 SBT Toán 10 - Cánh Diều
Trong các phát biểu sau, phát biểu nào sai?
A.\({(a + b)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}\)
B. \({(a - b)^4} = {a^4} - 4{a^3}b + 6{a^2}{b^2} - 4a{b^3} + {b^4}\)
C. \({(a + b)^4} = {b^4} + 4{b^3}a + 6{a^2}{b^2} - 4b{a^3} + {a^4}\)
D. \({(a + b)^4} = {a^4} + {b^4}\)
Phương pháp:
Áp dụng nhị thức Newton để khai triển \({(a + b)^4}\)và \({(a - b)^4} = {\left[ {a + ( - b)} \right]^4}\) để tìm câu đúng
Lời giải:
Đáp án đúng là D
Công thức khai triển nhị thức Newton (a + b)4 là:
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4 = b4 + 4b3a + 6b2a2 + 4ba3 + a4.
Do đó phương án A, C đúng, phương án D sai.
Công thức khai triển nhị thức Newton (a – b)4 là:
(a + b)4 = a4 – 4a3b + 6a2b2 – 4ab3 + b4.
Do đó phương án B đúng.
Vậy ta chọn phương án D.
Bài 29 trang 16 SBT Toán 10 - Cánh Diều
Trong các phát biểu sau, phát biểu nào đúng?
A.\({(a + b)^5} = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}\)
B. \({(a - b)^5} = {a^5} - 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} - 5a{b^4} + {b^5}\)
C. \({(a + b)^5} = {a^5} + {b^5}\)
D. \({(a - b)^5} = {a^5} - {b^5}\)
Phương pháp:
Áp dụng nhị thức Newton để khai triển \({(a + b)^5}\) để tìm câu đúng
Lời giải:
Công thức khai triển nhị thức Newton (a + b)5 là:
(a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5.
Do đó phương án A đúng, phương án C sai.
Công thức khai triển nhị thức Newton (a – b)5 là:
(a – b)5 = a5 – 5a4b + 10a3b2 – 10a2b3 + 5ab4 – b5.
Do đó các phương án B, D sai.
Vậy ta chọn phương án A.
Bài 30 trang 16 SBT Toán 10 - Cánh Diều
Hệ số của \({x^3}\) trong khai triển biểu thức \({(2x - 1)^4}\) là:
A. 32 B. -32 C. 8 D. -8
Phương pháp:
Áp dụng công thức khai triển: \({(a - b)^4} = {a^4} - 4{a^3}b + 6{a^2}{b^2} - 4a{b^3} + {b^4}\) với a = 2x và b = 1
Lời giải:
Đáp án đúng là B
Ta có: (2x – 1)4 = (2x)4 – 4.(2x)3.1 + 6.(2x)2.12 – 4.(2x).13 + 14
= 16x4 – 32x3 + 24x2 – 8x + 1
Số hạng chứa x3 trong khai triển biểu thức (2x – 1)4 là –32x3.
Vậy hệ số của x3 trong khai triển biểu thức (2x – 1)4 là –32.
Do đó ta chọn phương án B.
Bài 31 trang 16 SBT Toán 10 - Cánh Diều
Hệ số của x trong khai triển biểu thức \({(x - 2)^5}\) là:
A. 32 B. -32 C. 80 D. -80
Phương pháp:
Áp dụng công thức khai triển: \({(a + b)^5} = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}\) với a = 1 và b = -2
Lời giải:
Đáp án đúng là C
Ta có: (x – 2)5 = x5 – 5x4.2 + 10x3.22 – 10x2.23 + 5x.24 – 25
= x5 – 10x4 + 40x3 – 80x2 + 80x – 32
Số hạng chứa x trong khai triển biểu thức (x – 2)5 là 80x.
Vậy hệ số của x trong khai triển biểu thức (x – 2)5 là 80.
Do đó ta chọn phương án C.
Bài 32 trang 16 SBT Toán 10 - Cánh Diều
Khai triển các biểu thức sau:
a) \({(4x + 1)^4}\) b) \({(5x - 3)^4}\) c) \({\left( {\frac{1}{3}x + 5} \right)^5}\) d) \({\left( {3x - \frac{1}{3}} \right)^5}\)
Phương pháp:
Áp dụng các công thức khai triển:
Lời giải:
a) (4x + 1)4 = (4x)4 + 4.(4x)3.1 + 6.(4x)2.12 + 4.4x.13 + 14
= 256x4 + 256x3 + 96x2 + 16x + 1.
b) (5x – 3)4 = (5x)4 + 4.(5x)3.(–3) + 6.(5x)2.(–3)2 + 4.5x.(–3)3 + (–3)4
= 625x4 – 1500x3 + 1350x2 – 540x + 81.
Bài 33 trang 16 SBT Toán 10 - Cánh Diều
Xác định hệ số của \({x^2}\) trong khai triển biểu thức \({(4x - 3)^4}\)
Phương pháp:
Áp dụng công thức khai triển: \({(a - b)^4} = {a^4} - 4{a^3}b + 6{a^2}{b^2} - 4a{b^3} + {b^4}\)
Lời giải:
Ta có: (4x – 3)4 = (4x)4 – 4.(4x)3.3 + 6.(4x)2.32 – 4.4x.33 + 34
= 256x4 – 768x3 + 864x2 – 432x + 81
Số hạng chứa x2 trong khai triển biểu thức (4x – 3)4 là 864x2.
Vậy hệ số của x2 trong khai triển biểu thức (4x – 3)4 là 864.
Bài 34 trang 16 SBT Toán 10 - Cánh Diều
Xác định hệ số của \({x^3}\) trong khai triển biểu thức \({\left( {\frac{2}{3}x + \frac{1}{4}} \right)^5}\)
Phương pháp:
Áp dụng công thức khai triển \({(a + b)^5} = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}\)
Lời giải:
Ta có:
Bài 35 trang 16 SBT Toán 10 - Cánh Diều
Cho \({\left( {2x - \frac{1}{3}} \right)^4} = {a_0} + {a_1}x + {a_2}{x^2} + {a_3}{x^3} + {a_4}{x^4}\). Tính:
a) \({a_2}\)
b) \({a_0} + {a_1} + {a_2} + {a_3} + {a_4}\)
Phương pháp:
Bước 1: Áp dụng công thức khai triển: \({(a - b)^4} = {a^4} - 4{a^3}b + 6{a^2}{b^2} - 4a{b^3} + {b^4}\) với \(a = 2x,b = \frac{1}{3}\)
Bước 2: Thay x = 1 vào khai triển trong giả thiết để tính tổng các hệ số của khai triển
Lời giải:
a) Ta có:
Bài 36 trang 16 SBT Toán 10 - Cánh Diều
Cho \({\left( {\frac{3}{5}x + \frac{1}{2}} \right)^5} = {a_0} + {a_1}x + {a_2}{x^2} + {a_3}{x^3} + {a_4}{x^4} + {a_5}{x^5}\). Tính:
a) \({a_3}\)
b) \({a_0} + {a_1} + {a_2} + {a_3} + {a_4} + {a_5}\)
Phương pháp:
Bước 1: Áp dụng công thức khai triển: \({(a + b)^5} = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}\) với \(a = \frac{3}{5}x,b = \frac{1}{2}\)
Bước 2: Thay x = 1 vào khai triển trong giả thiết để tính tổng các hệ số của khai triển
Lời giải:
Ta có:
Bài 37 trang 16 SBT Toán 10 - Cánh Diều
Tính các tổng sau (Không sử dụng máy tính cầm tay):
a) \(T = C_4^0 + \frac{1}{2}C_4^1 + \frac{1}{3}C_4^2 + \frac{1}{4}C_4^3 + \frac{1}{5}C_4^4\)
b) \(S = C_6^1 + 2C_6^2 + 3C_6^3 + 4C_6^4 + 5C_5^6 + 6C_6^6\)
Phương pháp:
Bước 1: Ở ý a) áp dụng kết quả \(\frac{1}{{k + 1}}C_n^k = \frac{1}{{n + 1}}C_{n + 1}^{k + 1}\) với \(0 \le k \le n\) (chứng minh ở Bài 27a trang 14 SBT Toán 10 tập 2) và khai triển (a + b)5 với a = 1 và b = 1
Bước 2: Ở ý b) áp dụng kết quả \(kC_n^k = nC_{n - 1}^{k - 1}\) với \(1 \le k \le n\) (chứng minh ở Bài 27a trang 14 SBT Toán 10 tập 2) và khai triển (a + b)5 với a = 1 và b = 1
Lời giải:
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài tập cuối chương VII
- Bài 6. Ba đường conic
- Bài 5. Phương trình đường tròn
- Bài 4. Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng
- Bài 3. Phương trình đường thẳng
- Bài 2. Biểu thức tọa độ của các phép toán vectơ
- Bài 1. Tọa độ của vectơ
- Chương VII. Phương pháp tọa độ trong mặt phẳng
- Bài tập cuối chương VI
- Bài 5. Xác suất của biến cố
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!