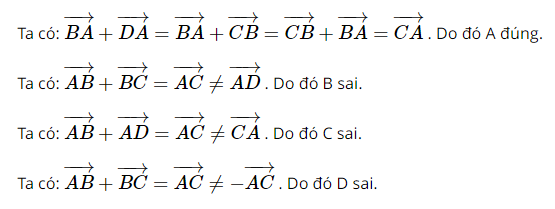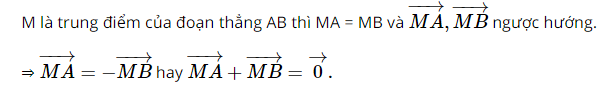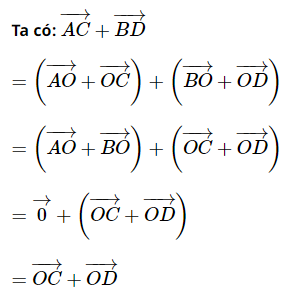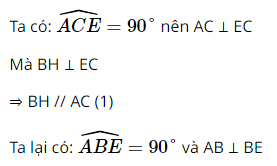Giải SBT Toán 10 trang 92, 93 Cánh Diều tập 1

Bài 32 trang 92 SBT Toán 10 - Cánh Diều

Cho ba điểm M, N, P phân biệt. Phát biểu nào sau đây là đúng?

A. \(\overrightarrow {MN}  - \overrightarrow {NP}  = \overrightarrow {MP} \)      

B. \( - \overrightarrow {MN}  + \overrightarrow {NP}  = \overrightarrow {MP} \)

C. \(\overrightarrow {MN}  + \overrightarrow {NP}  = \overrightarrow {MP} \)      

D. \(\overrightarrow {MN}  + \overrightarrow {NP}  =  - \overrightarrow {MP} \)

Lời giải:

Ta có: \(\overrightarrow {MN}  + \overrightarrow {NP}  = \overrightarrow {MP} \) 

Chọn C

Bài 33 trang 92 SBT Toán 10 - Cánh Diều

Cho tứ giác ABCD là hình bình hành. Khẳng định nào sau đây là đúng?

A. \(\overrightarrow {BA}  + \overrightarrow {DA}  = \overrightarrow {CA} \)

B. \(\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AD} \)

C. \(\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {CA} \)      

D. \(\overrightarrow {AB}  + \overrightarrow {BC}  =  - \overrightarrow {AC} \)

Lời giải:

Đáp án đúng là A

Bài 34 trang 92 SBT Toán 10 - Cánh Diều

Cho các điểm A, B, O. Khẳng định nào sau đây là đúng?

A. \(\overrightarrow {AB}  = \overrightarrow {OA}  - \overrightarrow {OB} \)      

B. \(\overrightarrow {AB}  = \overrightarrow {OB}  - \overrightarrow {OA} \)

C. \(\overrightarrow {AB}  = \overrightarrow {OA}  + \overrightarrow {OB} \)

D. \(\overrightarrow {AB}  = \overrightarrow {OB}  + \overrightarrow {OA} \) 

Lời giải:

Với 3 điểm A, B, O  ta có: \(\overrightarrow {AB}  = \overrightarrow {OB}  - \overrightarrow {OA} \)

Chọn B

Bài 35 trang 92 SBT Toán 10 - Cánh Diều

Cho ba điểm A, B, M phân biệt. Điều kiện cần và đủ để điểm M là trung điểm của đoạn thẳng AB là:

A. \(\overrightarrow {MA}  = \overrightarrow {MB} \)  

B. \(\left| {\overrightarrow {MA} } \right| = \left| {\overrightarrow {MB} } \right|\)

C. \(\overrightarrow {MA} ,\overrightarrow {MB} \) ngược hướng

D. \(\overrightarrow {MA}  + \overrightarrow {MB}  = \overrightarrow 0 \) 

Lời giải:

Đáp án đúng là D

Vậy điều kiện đủ đề M là trung điểm của đoạn thẳng AB là

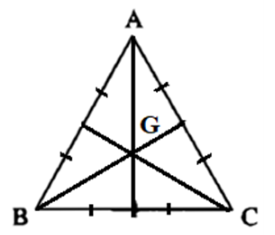
Bài 36 trang 92 SBT Toán 10 - Cánh Diều

Cho tam giác ABC. Điều kiện cần và đủ để điểm G là trọng tâm tam giác ABC là:

A. \(\overrightarrow {GA}  + \overrightarrow {GB}  = \overrightarrow {GC} \)      

B. \(\overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow {AG} \)

C. \(\overrightarrow {GC}  + \overrightarrow {GA}  = \overrightarrow {GB} \)      

D. \(\overrightarrow {GA}  + \overrightarrow {GB}  - \overrightarrow {GC}  = \overrightarrow 0 \)

Lời giải:

Ta có: Điều kiện cần và đủ để điểm G là trọng tâm tam giác ABC là \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \)

\( \Leftrightarrow \overrightarrow {GB}  + \overrightarrow {GC}  =  - \overrightarrow {GA}  \Leftrightarrow \overrightarrow {GB}  + \overrightarrow {GC}  = \ovaerrightarrow {AG} \)

Chọn B

Bài 37 trang 92 SBT Toán 10 - Cánh Diều

Cho tứ giác ABCD, O là trung điểm của AB. Chứng minh \(\overrightarrow {OC}  + \overrightarrow {OD}  = \overrightarrow {AC}  + \overrightarrow {BD} \)(*)

Lời giải:

Bài 38 trang 92 SBT Toán 10 - Cánh Diều

Cho tam giác ABC vuông tại A, \(AB = 4a,AC = 5a\). Tính

a)  \(\left| {\overrightarrow {AB}  - \overrightarrow {AC} } \right|\)          

b) \(\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right|\)

Lời giải:

∆ABC vuông tại A,  \(AB = 4a,AC = 5a\) \( \Rightarrow BC = \sqrt {A{B^2} + A{C^2}}  = a\sqrt {41} \)

a) Ta có: \(\left| {\overrightarrow {AB}  - \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} } \right| = BC = a\sqrt {41} \)

b) Dựng hình chữ nhật ABCD. Khi đó \(AD = BC = a\sqrt {41} \)

Ta có: \(\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD = a\sqrt {41} \)

Bài 39 trang 92 SBT Toán 10 - Cánh Diều

Cho tam giác đều ABC cạnh a. Tính:

a)  \(\left| {\overrightarrow {AB}  + \overrightarrow {BC} } \right|\)          

b) \(\left| {\overrightarrow {AB}  - \overrightarrow {AC} } \right|\)           

c) \(\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right|\)

Phương pháp:

Bước 1: Lấy G là trọng tâm tam giác ABC

Bước 2: Sử dụng quy tắc cộng, quy tắc trừ, quy tắc 3 điểm (lấy G là điểm trung gian) để biến đổi và tính độ dài các vectơ tương ứng

Lời giải:

Gọi G là trọng tâm tam giác ABC

Khi đó \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \), \(GA = GB = GC = \frac{{a\sqrt 3 }}{3}\)

a) Ta có: \(\left| {\overrightarrow {AB}  + \overrightarrow {BC} } \right| = \left| {\overrightarrow {AC} } \right| = AC = a\)

b) Ta có: \(\left| {\overrightarrow {AB}  - \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} } \right| = BC = a\)

c) Ta có: \(\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {\left( {\overrightarrow {GB}  - \overrightarrow {GA} } \right) + \left( {\overrightarrow {GC}  - \overrightarrow {GA} } \right)} \right| = \left| {\left( {\overrightarrow {GB}  + \overrightarrow {GC} } \right) - 2\overrightarrow {GA} } \right|\) (1)

Lại có: \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0  \Leftrightarrow \overrightarrow {GB}  + \overrightarrow {GC}  =  - \overrightarrow {GA} \) (2)

Từ (1) và (2) suy ra \(\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| { - \overrightarrow {GA}  - 2\overrightarrow {GA} } \right| = \left| { - 3\overrightarrow {GA} } \right| = 3\left| {\overrightarrow {GA} } \right| = 3GA = 3.\frac{{a\sqrt 3 }}{3} = a\sqrt 3 \)

Bài 40 trang 92 SBT Toán 10 - Cánh Diều

Cho tam giác ABC thỏa mãn \(\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AB}  - \overrightarrow {AC} } \right|\) (*). Chứng minh tam giác ABC vuông tại A.

Phương pháp:

Bước 1: Dựng hình bình hành ABDC

Bước 2: Sử dụng quy tắc trừ hai vectơ và quy tắc hình bình hành để biến đổi giả thiết (*)

Bước 3: Sử dụng dấu hiệu nhận biết hình chữ nhật để chứng minh tam giác ABC vuông tại A

Lời giải:

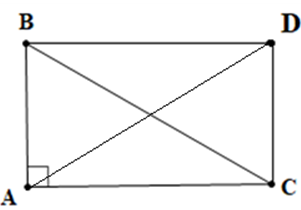
Dựng hình bình hành ABDC. Khi đó  \(\overrightarrow {AB}  + \overrightarrow {AC}  = \overrightarrow {AD} \)

Ta có: \(\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AB}  - \overrightarrow {AC} } \right| \Leftrightarrow \left| {\overrightarrow {AD} } \right| = \left| {\overrightarrow {CB} } \right| \Leftrightarrow AD = BC\)

\( \Rightarrow \) Hình bình hành ABCD có hai đường chéo bằng nhau nên là hình chữ nhật

\( \Rightarrow \widehat {BAC} = {90^0}\). Vậy tam giác ABC vuông tại A (ĐPCM)

Bài 41 trang 93 SBT Toán 10 - Cánh Diều

Cho hai vectơ \(\overrightarrow a ,\overrightarrow b \) khác vectơ \(\overrightarrow 0 \). Chứng minh rằng nếu hai vectơ cùng hướng thì \(\left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| = \left| {\overrightarrow a  + \overrightarrow b } \right|\)

Lời giải:

Lấy một điểm A trên mặt phẳng. Dựng \(\overrightarrow {AB}  = \overrightarrow a ,\overrightarrow {BC}  = \overrightarrow b \) sao cho \(\overrightarrow {AB} ,\overrightarrow {BC} \)cùng hướng

\( \Rightarrow \left| {\overrightarrow a } \right| = AB,\left| {\overrightarrow b } \right| = BC\)

Ta có: \(\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC}  \Leftrightarrow \overrightarrow a  + \overrightarrow b  = \overrightarrow {AC} \)

Lại có: AB + BC = AC \( \Rightarrow \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| = AC = \left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow a  + \overrightarrow b } \right|\)  (ĐPCM)

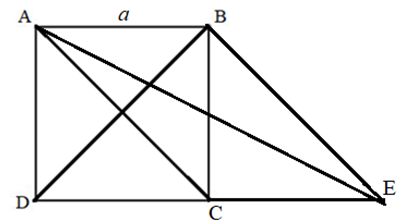
Bài 42 trang 93 SBT Toán 10 - Cánh Diều

Cho hình vuông ABCD cạnh a. Tính \(\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right|\)

Lời giải:

Dựng hình bình hành ABEC. Khi đó \(\overrightarrow {AB}  + \overrightarrow {AC}  = \overrightarrow {AE} \)

Ta có: \(\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AE} } \right| = AE\)

Xét tam giác ADE vuông tại D có \(AE = \sqrt {A{D^2} + D{E^2}}  = \sqrt {{a^2} + {{(2a)}^2}}  = \sqrt {5{a^2}}  = a\sqrt 5 \)

Vậy \(\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = AE = a\sqrt 5 \)

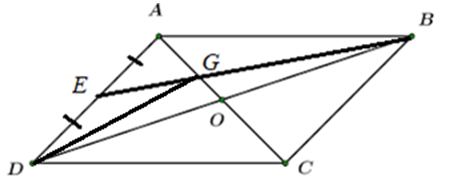
Bài 43 trang 93 SBT Toán 10 - Cánh Diều

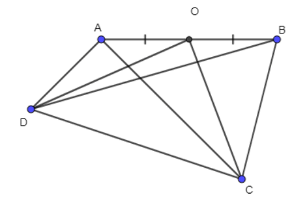
Cho tứ giác ABCD là hình bình hành. Gọi O là giao điểm của hai đường chéo , E là trung điểm của AD, G là giao điểm của BE và AC. Tính:

a) \(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD} \)           

b) \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GD} \)

Lời giải:

a) Do ABCD là hình bình hành nên O là trung điểm AC và BD

\( \Rightarrow \overrightarrow {OA}  + \overrightarrow {OC}  = \overrightarrow 0 ,\overrightarrow {OB}  + \overrightarrow {OD}  = \overrightarrow 0 \) \(\begin{array}{l} \Rightarrow \overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD}  = \left( {\overrightarrow {OA}  + \overrightarrow {OC} } \right) + \left( {\overrightarrow {OB}  + \overrightarrow {OD} } \right)\\ = \overrightarrow 0  + \overrightarrow 0  = \overrightarrow 0 \end{array}\)

b) Xét tam giác ABD có AO và BE là hai đường trung tuyến cắt nhau tại G

\( \Rightarrow \) G là trọng tâm ∆ABD \( \Rightarrow \overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GD}  = \overrightarrow 0 \)

Bài 44 trang 93 SBT Toán 10 - Cánh Diều

 Cho tam giác ABC. Tìm tập hợp các điểm M trong mặt phẳng thỏa mãn \(\left| {\overrightarrow {AB}  + \overrightarrow {BM} } \right| = \left| {\overrightarrow {AC}  - \overrightarrow {AM} } \right|\)

Phương pháp:

Sử dụng các quy tắc cộng, trừ 2 vectơ để biến đổi giả thiết rồi kết luận

Lời giải:

Ta có: \(\left| {\overrightarrow {AB}  + \overrightarrow {BM} } \right| = \left| {\overrightarrow {AC}  - \overrightarrow {AM} } \right| \Leftrightarrow \left| {\overrightarrow {AM} } \right| = \left| {\overrightarrow {MC} } \right| \Leftrightarrow AM = MC\)

Vậy tập hợp các điểm M cần tìm là đường trung trực của đoạn thẳng AC

Bài 45 trang 93 SBT Toán 10 - Cánh Diều

Cho hai tam giác ABC và A’B’C’ có cùng trọng tâm là G. Chứng minh \(\overrightarrow {AA'}  + \overrightarrow {BB'}  + \overrightarrow {CC'}  = \overrightarrow 0 \)

Phương pháp:

Sử dụng tính chất trọng tâm tam giác, quy tắc 3 điểm (lấy G là điểm trung gian) để biến đổi \(\overrightarrow {AA'}  + \overrightarrow {BB'}  + \overrightarrow {CC'} \) rồi kết luận

Lời giải:

Do G là trọng tâm tam giác ABC và tam giác A’B’C’ nên: \(\left\{ \begin{array}{l}\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \\\overrightarrow {GA'}  + \overrightarrow {GB'}  + \overrightarrow {GC'}  = \overrightarrow 0 \end{array} \right.\)

Ta có: \(\overrightarrow {AA'}  + \overrightarrow {BB'}  + \overrightarrow {CC'}  = \overrightarrow {GA'}  - \overrightarrow {GA}  + \overrightarrow {GB'}  - \overrightarrow {GB}  + \overrightarrow {GC'}  - \overrightarrow {GC} \)

                                  \( = \left( {\overrightarrow {GA'}  + \overrightarrow {GB'}  + \overrightarrow {GC'} } \right) - \left( {\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC} } \right)\)\( = \overrightarrow 0  - \overrightarrow 0  = \overrightarrow 0 \) (ĐPCM)

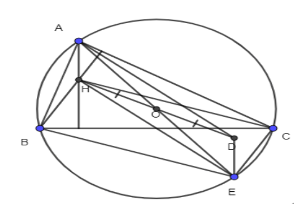
Bài 46 trang 93 SBT Toán 10 - Cánh Diều

Cho tam giác nhọn ABC có các cạnh đôi một khác nhau. Gọi H, O lần lượt là trực tâm và tâm đường tròn ngoại tiếp của tam giác, D là điểm đối xứng với H qua O. Chứng minh \(\overrightarrow {HA}  + \overrightarrow {HB}  + \overrightarrow {HC}  = \overrightarrow {HD} \)

Lời giải:

Vẽ đường kính AE

Mà CH ⊥ AB

⇒ BE // CH (2)

Từ (1) và (2) suy ra BHEC là hình bình hành

Xét tứ giác AHDE, có:

O là trung điểm của HD (gt)

O là trung điểm của AE

Do đó AHDE là hình bình hành

Khi đó, ta có:

 Sachbaitap.com