Giải SGK Toán 11 Chân trời sáng tạo tập 2 trang 41
Giải bài 1, 2, 3, 4, 5, 6 trang 41 SGK Toán lớp 11 Chân trời sáng tạo tập 2. Một người gửi tiết kiệm khoản tiền 10 triệu đồng vào một ngân hàng với lãi suất 5%/năm. Tính tổng số tiền vốn và lãi mà người đó nhận được sau một năm, nếu tiền lãi được tính theo thể thức:
Bài 1 trang 41 SGK Toán 11 - Chân trời sáng tạo tập 2
Dùng định nghĩa để tính đạo hàm của các hàm số sau:
a) \(f\left( x \right) = - {x^2}\);
b) \(f\left( x \right) = {x^3} - 2x\);
c) \(f\left( x \right) = \frac{4}{x}\).
Phương pháp:
Tính giới hạn \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\).
Lời giải:
a) Với bất kì x0 ∈ ℝ, ta có:
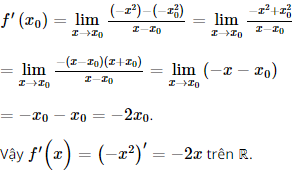
b) Với bất kì x0 ∈ ℝ, ta có:
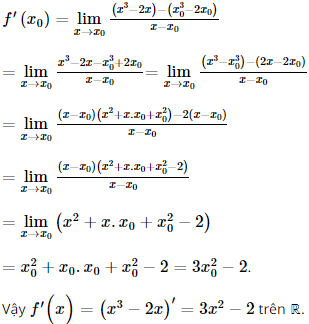
c) Với bất kì x0 ≠ 0, ta có:
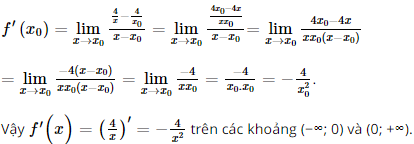
Bài 2 trang 41 SGK Toán 11 - Chân trời sáng tạo tập 2
Cho hàm số \(f\left( x \right) = - 2{x^2}\) có đồ thị \(\left( C \right)\) và điểm \(A\left( {1; - 2} \right) \in \left( C \right)\). Tính hệ số góc của tiếp tuyến với \(\left( C \right)\) tại điểm \(A\).
Phương pháp:
Hệ số góc: \(f'\left( {{x_0}} \right)\).
Lời giải:
Hệ số góc của tiếp tuyến với (C) tại điểm A là:
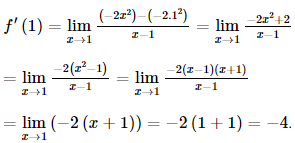
Vậy hệ số góc của tiếp tuyến với (C) tại điểm A là −4.
Bài 3 trang 41 SGK Toán 11 - Chân trời sáng tạo tập 2
Viết phương trình tiếp tuyến của đồ thị hàm số \(y = {x^3}\)
a) Tại điểm \(\left( { - 1;1} \right)\);
b) Tại điểm có hoành độ bằng 2.
Phương pháp:
Hệ số góc: \(f'\left( {{x_0}} \right)\).
Phương trình tiếp tuyến: \(y - f\left( {{x_0}} \right) = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right)\).
Lời giải:
Ta có: (x3)′=3x2.
a) Vì điểm M(−1; 1) không thuộc đồ thị hàm số (C) nên không có phương trình tiếp tuyến tại điểm M(−1; 1).
b) Với x0=2⇔y0=23=8. Do đó N(2;8).
Tiếp tuyến của (C) tại điểm N(2;8) có hệ số góc là: f′(2)=3.22=12.
Phương trình tiếp tuyến của (C) tại điểm N là: y–8=12(x−2)⇔y=12x–24+8⇔y=12x–16.
Bài 4 trang 41 SGK Toán 11 - Chân trời sáng tạo tập 2
Một chuyển động thẳng xác định bởi phương trình \(s\left( t \right) = 4{t^3} + 6t + 2\), trong đó \(s\) tính bằng mét và \(t\) là thời gian tính bằng giây. Tính vận tốc tức thời của chuyển động tại \(t = 2\).
Phương pháp:
Vận tốc tức thời của chuyển động tại thời điểm \({t_0}\) là: \(v\left( {{t_0}} \right) = s'\left( {{t_0}} \right)\)
Lời giải:
Vận tốc tức thời của chuyển động tại t = 2 là:
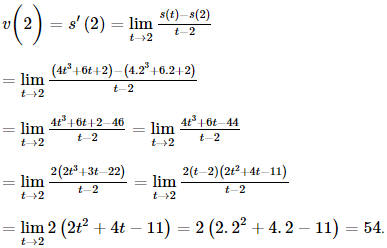
Vậy vận tốc tức thời của chuyển động lúc t = 2 là v(2) = 54 m/s.
Bài 5 trang 41 SGK Toán 11 - Chân trời sáng tạo tập 2
Một người gửi tiết kiệm khoản tiền 10 triệu đồng vào một ngân hàng với lãi suất 5%/năm. Tính tổng số tiền vốn và lãi mà người đó nhận được sau một năm, nếu tiền lãi được tính theo thể thức:
a) Lãi kép với kì hạn 6 tháng;
b) Lãi kép liên tục.
Phương pháp:
a) Sử dụng công thức \(T = A.{\left( {1 + \frac{r}{n}} \right)^n}\).
b) Sử dụng công thức \(T = A.{e^{rt}}\).
Lời giải:
a) Nếu tiền lãi được tính theo thể thức lãi kép với kì hạn 6 tháng.
Tổng số tiền vốn và lãi người đó nhận được sau 1 năm là:
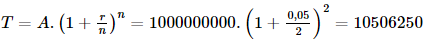 (đồng).
(đồng).
Vậy tổng số tiền vốn và lãi người đó nhận được sau 1 năm là 10 506 250 đồng, nếu tiền lãi được tính theo thể thức lãi kép với kì hạn 6 tháng.
b) Nếu tiền lãi được tính theo thể thức lãi kép liên tục.
Tổng số tiền vốn và lãi người đó nhận được sau 1 năm là:
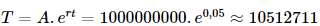 (đồng).
(đồng).
Vậy tổng số tiền vốn và lãi người đó nhận được sau 1 năm là 10 512 711 đồng, nếu tiền lãi được tính theo thể thức lãi kép liên tục.
Bài 6 trang 41 SGK Toán 11 - Chân trời sáng tạo tập
Một người gửi tiết kiệm khoản tiền 10 triệu đồng vào một ngân hàng với lãi suất 5%/năm. Tính tổng số tiền vốn và lãi mà người đó nhận được sau một năm, nếu tiền lãi được tính theo thể thức:
a) Lãi kép với kì hạn 6 tháng;
b) Lãi kép liên tục.
Phương pháp:
a) Sử dụng công thức \(T = A.{\left( {1 + \frac{r}{n}} \right)^n}\).
b) Sử dụng công thức \(T = A.{e^{rt}}\).
Lời giải:

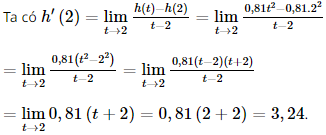
Vậy vận tốc tức thời của chuyển động lúc t = 2 là v(2) = h' (2) = 3,24 m/s.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài tập cuối chương 9
- Bài 2. Biến cố hợp và quy tắc cộng xác suất
- Bài 1. Biến cố giao và quy tắc nhân xác suất
- CHƯƠNG IX. XÁC SUẤT
- Bài tập cuối chương 8
- Bài 5. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
- Bài 4. Khoảng cách trong không gian
- Bài 3. Hai mặt phẳng vuông góc
- Bài 2. Đường thẳng vuông góc với mặt phẳng
- Bài 1. Hai đường thẳng vuông góc
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
