Giải SGK Toán 11 Chân trời sáng tạo tập 2 trang 48, 49
Giải bài 1, 2, 3, 4, 5, 6, 7 trang 48, 49 SGK Toán lớp 11 Chân trời sáng tạo tập 2. Trên Mặt Trăng, quãng đường rơi tự do của một vật được cho bởi công thức s(t) = 0,8 t2, trong đó t là thời gian được tính bằng giây và \({\rm{s}}\) tính bằng mét. Một vật được thả rơi từ độ cao 200 m phía trên Mặt Trăng. Tại thời điểm \(t = 2\) sau khi thả vật đó, tính:
Bài 1 trang 48 SGK Toán 11 - Chân trời sáng tạo tập 2
Tính đạo hàm của các hàm số sau:
a) \(y = 2{{\rm{x}}^3} - \frac{{{x^2}}}{2} + 4{\rm{x}} - \frac{1}{3}\);
b) \(y = \frac{{ - 2{\rm{x}} + 3}}{{{\rm{x}} - 4}}\);
c) \(y = \frac{{{x^2} - 2{\rm{x}} + 3}}{{{\rm{x}} - 1}}\); d) \(y = \sqrt {5{\rm{x}}} \).
Phương pháp:
Áp dụng đạo hàm của tổng, hiệu, tích thương.
Lời giải:
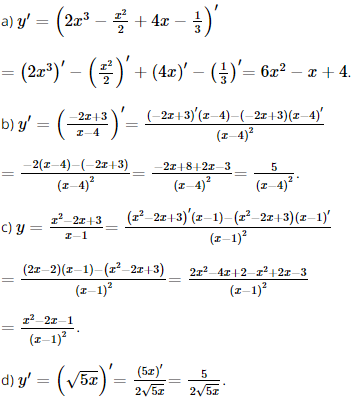
Bài 2 trang 49 SGK Toán 11 - Chân trời sáng tạo tập 2
Tính đạo hàm của các hàm số sau:
a) \(y = \sin 3x\);
b) \(y = {\cos ^3}2x\);
c) \(y = {\tan ^2}x\);
d) \(y = \cot \left( {4 - {x^2}} \right)\).
Phương pháp:
Sử dụng công thức tính đạo hàm của hàm hợp: \(y{'_x} = y{'_u}.u{'_x}\).
Lời giải:
a) y' = (sin3x)' = cos3x×(3x)' = 3cos3x.
b) y' = (cos32x)' = 3cos22x(cos2x)' = −6cos22xsin2x.
c) y' = (tan2x)' = 2tanx×(tanx)'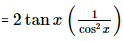 = 2tanx(1 + tan2x).
= 2tanx(1 + tan2x).
d) y' = [cot(4 – x2)]' =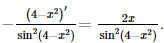
Bài 3 trang 49 SGK Toán 11 - Chân trời sáng tạo tập 2
Tính đạo hàm của các hàm số sau:
a) \(y = \left( {{x^2} - x} \right){.2^x}\);
b) \(y = {x^2}{\log _3}x\);
c) \(y = {e^{3x + 1}}\).
Phương pháp:
a) b) Sử dụng đạo hàm của tổng, hiệu, tích thương.
c) Sử dụng công thức tính đạo hàm của hàm hợp: \(y{'_x} = y{'_u}.u{'_x}\).
Lời giải:
a) y' = [(x2 – x)×2x]' = (x2 – x)'×2x + (x2 – x)×(2x)'
= (2x – 1)×2x + (x2 – x)×2x×ln2
= 2x(x2ln2 + 2x – 1 – xln2).
b) y' = (x2log3x)' = (x2)'log3x + x2(log3x)'
= 2xlog3x +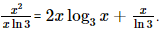
c) y' = (e3x + 1)' = e3x + 1×(3x + 1)' = 3e3x + 1.
Bài 4 trang 49 SGK Toán 11 - Chân trời sáng tạo tập 2
Tính đạo hàm cấp hai của các hàm số sau:
a) \(y = 2{x^4} - 5{x^2} + 3\);
b) \(y = x{e^x}\).
Phương pháp:
Tính \(y'\), sau đó tính y''.
Lời giải:
a) y' = (2x4 – 5x2 + 3)' = 8x3 – 10x.
y" = (8x3 – 10x)' = 24x2 – 10.
Vậy y" = 24x2 – 10.
b) y' = (xex)' = x'ex + x×(ex)' = ex + xex.
y" = (ex + xex)' = ex + ex + xex = 2ex + xex.
Vậy y" = 2ex + xex.
Bài 5 trang 49 SGK Toán 11 - Chân trời sáng tạo tập 2
Cân nặng trung bình của một bé gái trong độ tuổi từ 0 đến 36 tháng có thể được tính gần đúng bởi hàm số \(w\left( t \right) = 0,000758{t^3} - 0,0596{t^2} + 1,82t + 8,15\), trong đó \(t\) được tính bằng tháng và \(w\) được tính bằng pound (nguồn: https://www.cdc.gov/growthcharts/data/who/GrChrt_Boys). Tính tốc độ thay đổi cân nặng của bé gái đó tại thời điểm 10 tháng tuổi.
Phương pháp:
Tính \({\rm{w}}'\left( {10} \right)\).
Lời giải:
Tốc độ thay đổi cân nặng của bé gái đó tại thời điểm t là:
w'(t) = (0,000758t3 – 0,0596t2 + 1,82t + 8,15)' = 0,002274t2 – 0,1192t + 1,82.
Tốc độ thay đổi cân nặng của bé gái đó tại thời điểm 10 tháng tuổi là:
w'(10) = 0,002274×(10)2 – 0,1192×10 + 1,82. = 0,8554 (pound/tháng).
Vậy tốc độ thay đổi cân nặng của bé gái đó tại thời điểm 10 tháng tuổi là 0,8554 pound/tháng.
Bài 6 trang 49 SGK Toán 11 - Chân trời sáng tạo tập 2
Một công ty xác định rằng tổng chi phí của họ, tính theo nghìn đô-la, để sản xuất \(x\) mặt hàng là \(C\left( x \right) = \sqrt {5{x^2} + 60} \) và công ty lên kế hoạch nâng sản lượng trong \(t\) tháng kể từ nay theo hàm số \(x\left( t \right) = 20t + 40\). Chi phí sẽ tăng nhanh thế nào sau 4 tháng kể từ khi công ty thực hiện kế hoạch đó?
Phương pháp:
Tính \(C'\left( t \right)\) với \(t = 4\).
Lời giải:
Ta có 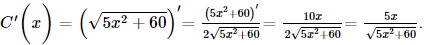
Có x'(t) = (20t + 40)' = 20; x(4) = 120.
Khi đó, tốc độ tăng chi phí của công ty sau t tháng là: C'(x(t)) = C'(x)×x'(t).
Tốc độ tăng chi phí của công ty sau 4 tháng kể từ khi công ty thực hiện kế hoạch đó là:
C'(x(4)) = C'(120)×x'(4) =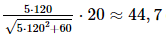 (nghìn đô-la/tháng).
(nghìn đô-la/tháng).
Tốc độ tăng chi phí của công ty sau 4 tháng kể từ khi công ty thực hiện kế hoạch đó khoảng 44,7 nghìn đô/tháng.
Bài 7 trang 49 SGK Toán 11 - Chân trời sáng tạo tập 2
Trên Mặt Trăng, quãng đường rơi tự do của một vật được cho bởi công thức \(s\left( t \right) = 0,81{t^2}\), trong đó \(t\) là thời gian được tính bằng giây và \({\rm{s}}\) tính bằng mét. Một vật được thả rơi từ độ cao 200 m phía trên Mặt Trăng. Tại thời điểm \(t = 2\) sau khi thả vật đó, tính:
a) Quãng đường vật đã rơi;
b) Gia tốc của vật.
Phương pháp:
a) Tính \(s\left( 2 \right)\).
b) Tính a(2) = s''(2).
Lời giải:
a) Quãng đường vật đã rơi tại thời điểm t = 2 là: s(2) = 0,81×22 = 3,24 (m).
Vậy sau 2 giây vật đã rơi được 3,24 m.
b) Có v(t) = s'(t) = (0,81t2)' = 1,62t.
a(t) = v'(t) = (1,62t)' = 1,62.
Vậy gia tốc của vật tại thời điểm t = 2 là 1,62 m/s2.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài tập cuối chương 9
- Bài 2. Biến cố hợp và quy tắc cộng xác suất
- Bài 1. Biến cố giao và quy tắc nhân xác suất
- CHƯƠNG IX. XÁC SUẤT
- Bài tập cuối chương 8
- Bài 5. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
- Bài 4. Khoảng cách trong không gian
- Bài 3. Hai mặt phẳng vuông góc
- Bài 2. Đường thẳng vuông góc với mặt phẳng
- Bài 1. Hai đường thẳng vuông góc
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
