Giải SGK Toán 11 trang 140, 141 Chân trời sáng tạo tập 1
Giải bài 1 trang 140, bài 2, 3, 4 trang 141 SGK Toán lớp 11 Chân trời sáng tạo tập 1. Lương tháng của một số nhân viên một văn phòng được ghi lại như sau (đơn vị: triệu đồng):
Bài 1 trang 140 SGK Toán 11 tập 1 - Chân trời sáng tạo
Lương tháng của một số nhân viên một văn phòng được ghi lại như sau (đơn vị: triệu đồng):

a) Tìm tứ phân vị của dãy số liệu trên.
b) Tổng hợp lại dãy số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:

c) Hãy ước lượng tứ phân vị của số liệu ở bảng tần số ghép nhóm trên.
Phương pháp:
a) Sắp xếp dãy số liệu theo thứ tự không giảm và tìm tứ phân vị.
b) Đếm và lập bảng.
c) Sử dụng công thức tính tứ phân vị.
Lời giải:
a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:

Tứ phân vị thứ nhất là: \(\frac{1}{2}\left( {{x_6} + {x_7}} \right) = \frac{1}{2}\left( {8,9 + 9,2} \right) = 9,05\)
Tứ phân vị thứ hai là: \(\frac{1}{2}\left( {{x_{13}} + {x_{14}}} \right) = \frac{1}{2}\left( {10,7 + 10,9} \right) = 10,8\)
Tứ phân vị thứ ba là: \(\frac{1}{2}\left( {{x_{18}} + {x_{19}}} \right) = \frac{1}{2}\left( {12,2 + 12,5} \right) = 12,35\)
b)

c) Tổng số nhân viên văn phòng là: \(n = 3 + 6 + 8 + 7 = 24\).
Gọi \({x_1};{x_2};...;{x_{24}}\) là lương tháng của các nhân viên văn phòng được xếp theo thứ tự không giảm.
Ta có:
\({x_1},{x_2},{x_3} \in \begin{array}{*{20}{l}}{\left[ {6;8} \right)}\end{array};{x_4},...,{x_9} \in \begin{array}{*{20}{l}}{\left[ {8;10} \right)}\end{array};{x_{10}},...,{x_{17}} \in \begin{array}{*{20}{l}}{\left[ {10;12} \right)}\end{array};{x_{18}},...,{x_{24}} \in \begin{array}{*{20}{l}}{\left[ {12;14} \right)}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{13}} + {x_{14}}} \right)\)
Ta có: \(n = 24;{n_m} = 8;C = 3 + 6 = 9;{u_m} = 10;{u_{m + 1}} = 12\)
Do \({x_{13}},{x_{14}} \in \begin{array}{*{20}{l}}{\left[ {10;12} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10 + \frac{{\frac{{24}}{2} - 9}}{8}.\left( {12 - 10} \right) = 10,75\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_6} + {x_7}} \right)\).
Ta có: \(n = 24;{n_m} = 6;C = 3;{u_m} = 8;{u_{m + 1}} = 10\)
Do \({x_6},{x_7} \in \begin{array}{*{20}{l}}{\left[ {8;10} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 8 + \frac{{\frac{{24}}{4} - 3}}{6}.\left( {10 - 8} \right) = 9\)
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{18}} + {x_{19}}} \right)\).
Ta có: \(n = 24;{n_j} = 7;C = 3 + 6 + 8 = 17;{u_j} = 12;{u_{j + 1}} = 14\)
Do \({x_{18}},{x_{19}} \in \begin{array}{*{20}{l}}{\left[ {12;14} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 12 + \frac{{\frac{{3.24}}{4} - 17}}{7}.\left( {14 - 12} \right) \approx 12,3\)
Bài 2 trang 141 SGK Toán 11 tập 1 - Chân trời sáng tạo
Số điểm một cầu thủ bóng rổ ghi được trong 20 trận đấu được cho ở bảng sau:

a) Tìm tứ phân vị của dãy số liệu trên.
b) Tổng hợp lại dãy số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:

c) Hãy ước lượng tứ phân vị của số liệu từ bảng tần số ghép nhóm trên.
Lời giải:
a) Sắp xếp dãy số liệu theo thứ tự không giảm ta được:
6; 8; 8; 10; 11; 11; 12; 13; 14; 14; 14; 15; 18; 18; 21; 22; 23; 24; 25; 25.

b) Ta có bảng tần số ghép nhóm theo mẫu sau:
|
Điểm số |
[6; 10] |
[11; 15] |
[16; 20] |
[21; 25] |
|
Số trận |
4 |
8 |
2 |
6 |
c) Ta có bảng hiểu chỉnh bảng trên như sau:
|
Điểm số |
[5,5; 10,5) |
[10,5; 15,5) |
[15,5; 20,5) |
[20,5; 25,5) |
|
Số trận |
4 |
8 |
2 |
6 |
Gọi x1; x2; ...; x20 là lương tháng của nhân viên một văn phòng theo thứ tự không giảm.
Ta có: x1; ...; x4 ∈ [5,5; 10,5), x5; ...; x12 ∈ [10,5; 15,5), x13; x14 ∈ [15,5; 20,5), x15; ...; x20 ∈ [20,5; 25,5).
Khi đó:

Bài 3 trang 141 SGK Toán 11 tập 1 - Chân trời sáng tạo
Kiểm tra điện lượng của một số viên pin tiểu do một hãng sản xuất thu được kết quả sau:

Hãy ước lượng số trung bình, mốt và tứ phân vị của mẫu số liệu ghép nhóm trên.
Lời giải:
Ta có:
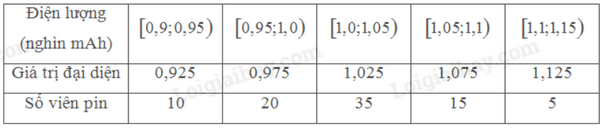
Tổng số viên pin là: \(n = 10 + 20 + 35 + 15 + 5 = 85\).
• Điện lượng trung bình của một số viên pin tiểu sau khi ghép nhóm là:
\(\bar x = \frac{{10.0,925 + 20.0,975 + 35.1,025 + 15.1,075 + 5.1,125}}{{85}} \approx 1,02\left( {mAh} \right)\)
• Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\begin{array}{*{20}{c}}{\left[ {1,0;1,05} \right)}\end{array}\).
Do đó: \({u_m} = 1,0;{n_{m - 1}} = 20;{n_m} = 35;{n_{m + 1}} = 15;{u_{m + 1}} - {u_m} = 1,05 - 1,0 = 0,05\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 1,0 + \frac{{35 - 20}}{{\left( {35 - 20} \right) + \left( {35 - 15} \right)}}.0,05 \approx 1,02\left( {mAh} \right)\)
Gọi \({x_1};{x_2};...;{x_{85}}\) là điện lượng của các viên pin được xếp theo thứ tự không giảm.
Ta có:
\(\begin{array}{l}{x_1},...,{x_{10}} \in \begin{array}{*{20}{c}}{\left[ {0,9;0,95} \right)}\end{array};{x_{11}},...,{x_{30}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {0,95;1,0} \right)}\end{array}}\end{array};{x_{31}},...,{x_{65}} \in \begin{array}{*{20}{c}}{\left[ {1,0;1,05} \right)}\end{array};\\{x_{66}},...,{x_{80}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {1,05;1,1} \right)}\end{array}}\end{array};{x_{81}},...,{x_{85}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {1,1;1,15} \right)}\end{array}}\end{array}}\end{array}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \({x_{43}}\)
Ta có: \(n = 85;{n_m} = 35;C = 10 + 20 = 30;{u_m} = 1,0;{u_{m + 1}} = 1,05\)
Do \({x_{43}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {1,0;1,05} \right)}\end{array}}\end{array}}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 1,0 + \frac{{\frac{{85}}{2} - 30}}{{35}}.\left( {1,05 - 1,0} \right) \approx 1,02\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_{21}} + {x_{22}}} \right)\).
Ta có: \(n = 85;{n_m} = 20;C = 10;{u_m} = 0,95;{u_{m + 1}} = 1,0\)
Do \({x_{21}},{x_{22}} \in \begin{array}{*{20}{c}}{\left[ {0,95;1,0} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 0,95 + \frac{{\frac{{85}}{4} - 10}}{{20}}.\left( {1,0 - 0,95} \right) \approx 0,98\)
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{64}} + {x_{65}}} \right)\).
Ta có: \(n = 85;{n_j} = 35;C = 10 + 20 = 30;{u_j} = 1,0;{u_{j + 1}} = 1,05\)
Do \({x_{64}},{x_{65}} \in \begin{array}{*{20}{c}}{\left[ {1,0;1,05} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 1,0 + \frac{{\frac{{3.85}}{4} - 30}}{{35}}.\left( {1,05 - 1,0} \right) \approx 1,048\)
Bài 4 trang 141 SGK Toán 11 tập 1 - Chân trời sáng tạo
Cân nặng của một số lợn con mới sinh thuộc hai giống A và B được cho ở biểu đồ dưới đây (đơn vị: kg).
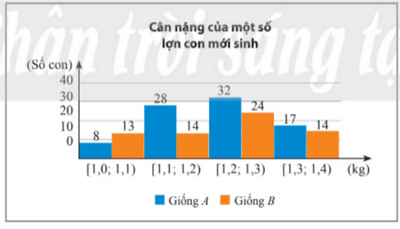
a) Hãy so sánh cân nặng của lợn con mới sinh giống A và giống B theo số trung bình và trung vị.
b) Hãy ước lượng tứ phân vị thứ nhất và thứ ba của cân nặng lợn con mới sinh giống A và của cân nặng lợn con mới sinh giống B.
Phương pháp:
Lập bảng tần số ghép nhóm rồi tính số trung bình, số trung vị, tứ phân vị thứ nhất và thứ ba theo bảng tần số ghép nhóm rồi so sánh.
Lời giải:
Ta có số liệu thống kê cân nặng của một số lợn con mới sinh thuộc hai giống A và B như sau:
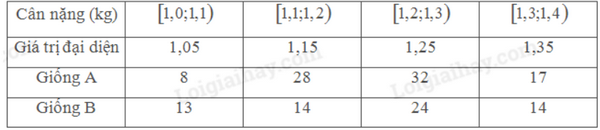
• Tổng số lợn con giống A là: \(n = 8 + 28 + 32 + 17 = 85\)
Cân nặng trung bình của lợn con giống A là:
\(\bar x = \frac{{8.1,05 + 28.1,15 + 32.1,25 + 17.1,35}}{{85}} \approx 1,22\left( {kg} \right)\)
Nhóm chứa số trung vị của giống A là: \(\begin{array}{*{20}{l}}{\;\left[ {1,2;1,3} \right)}\end{array}\)
Ta có: \(n = 85;{n_m} = 31;C = 8 + 28 = 36;{u_m} = 1,2;{u_{m + 1}} = 1,3\)
Trung vị của cân nặng của lợn con giống A là:
\({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 1,2 + \frac{{\frac{{85}}{2} - 31}}{{36}}.\left( {1,3 - 1,2} \right) \approx 1,23\left( {kg} \right)\)
• Tổng số lợn con giống B là: \(n = 13 + 14 + 24 + 14 = 65\)
Cân nặng trung bình của lợn con giống B là:
\(\bar x = \frac{{13.1,05 + 14.1,15 + 24.1,25 + 14.1,35}}{{65}} = 1,21\left( {kg} \right)\)
Nhóm chứa số trung vị của giống B là: \(\begin{array}{*{20}{l}}{\;\left[ {1,2;1,3} \right)}\end{array}\)
Ta có: \(n = 65;{n_m} = 24;C = 13 + 14 = 27;{u_m} = 1,2;{u_{m + 1}} = 1,3\)
Trung vị của cân nặng của lợn con giống B là:
\({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 1,2 + \frac{{\frac{{65}}{2} - 27}}{{24}}.\left( {1,3 - 1,2} \right) \approx 1,22\left( {kg} \right)\)
Vậy số cân nặng trung bình và số trung vị giống A lớn hơn giống B.
b) • Giống A
Gọi \({x_1};{x_2};...;{x_{85}}\) là cân nặng của các con lợn con được xếp theo thứ tự không giảm.
Ta có:
\({x_1},...,{x_8} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}{\;\left[ {1,0;1,1} \right)}\end{array}}\end{array};{x_9},...,{x_{36}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}{\;\left[ {1,1;1,2} \right)}\end{array}}\end{array}}\end{array};{x_{37}},...,{x_{68}} \in \begin{array}{*{20}{l}}{\;\left[ {1,2;1,3} \right)}\end{array};{x_{69}},...,{x_{85}} \in \begin{array}{*{20}{l}}{\;\left[ {1,3;1,4} \right)}\end{array}\)
Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_{21}} + {x_{22}}} \right)\).
Ta có: \(n = 85;{n_m} = 28;C = 8;{u_m} = 1,1;{u_{m + 1}} = 1,2\)
Do \({x_{21}},{x_{22}} \in \begin{array}{*{20}{c}}{\left[ {1,1;1,2} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 1,1 + \frac{{\frac{{85}}{4} - 8}}{{28}}.\left( {1,2 - 1,1} \right) \approx 1,15\)
Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{64}} + {x_{65}}} \right)\).
Ta có: \(n = 85;{n_j} = 32;C = 8 + 28 = 34;{u_j} = 1,2;{u_{j + 1}} = 1,3\)
Do \({x_{64}},{x_{65}} \in \begin{array}{*{20}{c}}{\left[ {1,2;1,3} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 1,2 + \frac{{\frac{{3.85}}{4} - 34}}{{32}}.\left( {1,3 - 1,2} \right) \approx 1,29\)
• Giống B
Gọi \({y_1};{y_2};...;{y_{65}}\) là cân nặng của các con lợn con được xếp theo thứ tự không giảm.
Ta có:
\({y_1},...,{y_{13}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}{\;\left[ {1,0;1,1} \right)}\end{array}}\end{array};{y_{14}},...,{y_{27}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}{\;\left[ {1,1;1,2} \right)}\end{array}}\end{array}}\end{array};{y_{28}},...,{y_{51}} \in \begin{array}{*{20}{l}}{\;\left[ {1,2;1,3} \right)}\end{array};{y_{52}},...,{y_{65}} \in \begin{array}{*{20}{l}}{\;\left[ {1,3;1,4} \right)}\end{array}\)
Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{y_{16}} + {y_{17}}} \right)\).
Ta có: \(n = 65;{n_m} = 14;C = 13;{u_m} = 1,1;{u_{m + 1}} = 1,2\)
Do \({y_{16}},{y_{17}} \in \begin{array}{*{20}{c}}{\left[ {1,1;1,2} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 1,1 + \frac{{\frac{{65}}{4} - 13}}{{14}}.\left( {1,2 - 1,1} \right) \approx 1,12\)
Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{y_{49}} + {y_{50}}} \right)\).
Ta có: \(n = 65;{n_j} = 24;C = 13 + 14 = 27;{u_j} = 1,2;{u_{j + 1}} = 1,3\)
Do \({y_{49}},{y_{50}} \in \begin{array}{*{20}{c}}{\left[ {1,2;1,3} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 1,2 + \frac{{\frac{{3.65}}{4} - 27}}{{24}}.\left( {1,3 - 1,2} \right) \approx 1,29\)
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài tập cuối chương 9
- Bài 2. Biến cố hợp và quy tắc cộng xác suất
- Bài 1. Biến cố giao và quy tắc nhân xác suất
- CHƯƠNG IX. XÁC SUẤT
- Bài tập cuối chương 8
- Bài 5. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
- Bài 4. Khoảng cách trong không gian
- Bài 3. Hai mặt phẳng vuông góc
- Bài 2. Đường thẳng vuông góc với mặt phẳng
- Bài 1. Hai đường thẳng vuông góc
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
