Giải SGK Toán 11 trang 50 Chân trời sáng tạo tập 1
Giải bài 1, 2, 3, 4, 5, 6, 7 trang 50 SGK Toán lớp 11 Chân trời sáng tạo tập 1. Trên lưới ô vuông, mỗi ô cạnh 1 đơn vị, người ta vẽ 8 hình vuông và tô màu khác nhau như Hình 3. Tìm dãy số biểu diễn độ dài cạnh của 8 hình vuông đỏ từ nhỏ đến lớn. Có nhận xét gì về dãy số trên?
Bài 1 trang 50 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tìm \({u_2},{u_3}\) và dự đoán công thức số hạng tổng quát \({u_n}\) của dãy số:
\(\left\{ \begin{array}{l}{u_1} = 1\\{u_{n + 1}} = \frac{{{u_n}}}{{1 + {u_n}}}\left( {n \ge 1} \right)\end{array} \right.\)
Phương pháp:
‒ Lần lượt thay giá trị \(n = 1;2;3\) vào biểu thức \({u_{n + 1}}\).
‒ Tìm điểm chung của các số hạng của dãy số \(\left( {{u_n}} \right)\).
Lời giải:
Ta có:
\(\begin{array}{l}{u_2} = \frac{{{u_1}}}{{1 + {u_1}}} = \frac{1}{{1 + 1}} = \frac{1}{2}\\{u_3} = \frac{{{u_2}}}{{1 + {u_2}}} = \frac{{\frac{1}{2}}}{{1 + \frac{1}{2}}} = \frac{1}{3}\end{array}\)
Suy ra, \({u_n} = \frac{1}{n}\)
Bài 2 trang 50 SGK Toán 11 tập 1 - Chân trời sáng tạo
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{1}{{1.2}} + \frac{1}{{2.3}} + ... + \frac{1}{{n\left( {n + 1} \right)}}\). Tìm \({u_1},{u_2},{u_3}\) và dự đoán công thức số hạng tổng quát \({u_n}\).
Phương pháp:
‒ Lần lượt thay giá trị \(n = 1;2;3\) vào biểu thức \({u_n}\).
‒ Tìm điểm chung của các số hạng của dãy số \(\left( {{u_n}} \right)\).
Lời giải:

Bài 3 trang 50 SGK Toán 11 tập 1 - Chân trời sáng tạo
Xét tính tăng, giảm của dãy số \(\left( {{y_n}} \right)\) với \({y_n} = \sqrt {n + 1} - \sqrt n \).
Phương pháp:
Bước 1: Tìm \({y_{n + 1}}\).
Bước 2: Xét hiệu \({y_{n + 1}} - {y_n}\) hoặc xét thương \(\frac{{{y_{n + 1}}}}{{{y_n}}}\) nếu các số hạng của dãy số \(\left( {{y_n}} \right)\) là số dương.
Bước 3: Kết luận:
– Nếu \({y_{n + 1}} - {y_n} > 0\) hoặc \(\frac{{{y_{n + 1}}}}{{{y_n}}} > 1\) thì \({y_{n + 1}} > {y_n},\forall n \in {\mathbb{N}^*}\), vậy dãy số \(\left( {{y_n}} \right)\) là dãy số tăng.
– Nếu \({y_{n + 1}} - {y_n} < 0\) hoặc \(\frac{{{y_{n + 1}}}}{{{y_n}}} < 1\) thì \({y_{n + 1}} < {y_n},\forall n \in {\mathbb{N}^*}\), vậy dãy số \(\left( {{y_n}} \right)\) là dãy số giảm.
Lời giải:
Cách 1:
Ta có: \({y_n} = \sqrt {n + 1} - \sqrt n = \frac{{\left( {\sqrt {n + 1} - \sqrt n } \right)\left( {\sqrt {n + 1} + \sqrt n } \right)}}{{\sqrt {n + 1} + \sqrt n }} = \frac{{\left( {n + 1} \right) - n}}{{\sqrt {n + 1} + \sqrt n }} = \frac{1}{{\sqrt {n + 1} + \sqrt n }}\)
\( \Rightarrow {y_{n + 1}} = \frac{1}{{\sqrt {\left( {n + 1} \right) + 1} - \sqrt {n + 1} }} = \frac{1}{{\sqrt {n + 2} + \sqrt {n + 1} }}\)
Xét hiệu:
\(\begin{array}{l}{y_{n + 1}} - {y_n} = \frac{1}{{\sqrt {n + 2} + \sqrt {n + 1} }} - \frac{1}{{\sqrt {n + 1} + \sqrt n }} = \frac{{\left( {\sqrt {n + 1} + \sqrt n } \right) - \left( {\sqrt {n + 2} + \sqrt {n + 1} } \right)}}{{\left( {\sqrt {n + 2} + \sqrt {n + 1} } \right)\left( {\sqrt {n + 1} + \sqrt n } \right)}}\\ = \frac{{\sqrt {n + 1} + \sqrt n - \sqrt {n + 2} - \sqrt {n + 1} }}{{\left( {\sqrt {n + 2} + \sqrt {n + 1} } \right)\left( {\sqrt {n + 1} + \sqrt n } \right)}} = \frac{{\sqrt n - \sqrt {n + 2} }}{{\left( {\sqrt {n + 2} + \sqrt {n + 1} } \right)\left( {\sqrt {n + 1} + \sqrt n } \right)}}\end{array}\)
\(\forall n \in {\mathbb{N}^*}\) ta có:
\(\begin{array}{l}\left. \begin{array}{l}0 < n < n + 2 \Leftrightarrow \sqrt n < \sqrt {n + 2} \Leftrightarrow \sqrt n - \sqrt {n + 2} < 0\\\sqrt {n + 2} > 0,\sqrt {n + 1} > 0,\sqrt n > 0 \Leftrightarrow \left( {\sqrt {n + 2} + \sqrt {n + 1} } \right)\left( {\sqrt {n + 1} + \sqrt n } \right) > 0\end{array} \right\}\\ \Rightarrow \frac{{\sqrt n - \sqrt {n + 2} }}{{\left( {\sqrt {n + 2} + \sqrt {n + 1} } \right)\left( {\sqrt {n + 1} + \sqrt n } \right)}} < 0\end{array}\)
Vậy \({y_{n + 1}} - {y_n} < 0 \Leftrightarrow {y_{n + 1}} < {y_n}\). Vậy dãy số \(\left( {{y_n}} \right)\) là dãy số giảm.
Cách 2:
Ta có: \({y_n} = \sqrt {n + 1} - \sqrt n = \frac{{\left( {\sqrt {n + 1} - \sqrt n } \right)\left( {\sqrt {n + 1} + \sqrt n } \right)}}{{\sqrt {n + 1} + \sqrt n }} = \frac{{\left( {n + 1} \right) - n}}{{\sqrt {n + 1} + \sqrt n }} = \frac{1}{{\sqrt {n + 1} + \sqrt n }}\)
\( \Rightarrow {y_{n + 1}} = \frac{1}{{\sqrt {\left( {n + 1} \right) + 1} - \sqrt {n + 1} }} = \frac{1}{{\sqrt {n + 2} + \sqrt {n + 1} }}\)
\(\forall n \in {\mathbb{N}^*}\) ta có:
\(\begin{array}{l}0 < n < n + 2 \Leftrightarrow \sqrt n < \sqrt {n + 2} \Leftrightarrow \sqrt {n + 1} + \sqrt n < \sqrt {n + 2} + \sqrt {n + 1} \\ \Leftrightarrow \frac{1}{{\sqrt {n + 1} + \sqrt n }} > \frac{1}{{\sqrt {n + 2} + \sqrt {n + 1} }} \Leftrightarrow {y_n} > {y_{n + 1}}\end{array}\)
Vậy dãy số \(\left( {{y_n}} \right)\) là dãy số giảm.
Bài 4 trang 50 SGK Toán 11 tập 1 - Chân trời sáng tạo
Xét tính bị chặn của các dãy số sau:
a) \(\left( {{a_n}} \right)\) với \({a_n} = {\sin ^2}\frac{{n\pi }}{3} + \cos \frac{{n\pi }}{4}\);
b) \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{6n - 4}}{{n + 2}}\)
Phương pháp:
a) Sử dụng tính chất của hàm lượng giác.
b) Sử dụng tính chất của bất đẳng thức.
Lời giải:
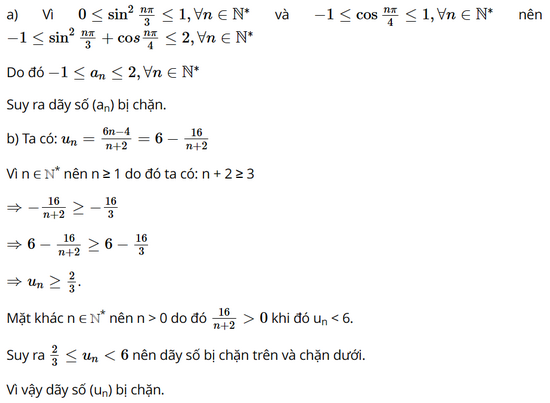
Bài 5 trang 50 SGK Toán 11 tập 1 - Chân trời sáng tạo
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{2n - 1}}{{n + 1}}\).
Chứng minh \(\left( {{u_n}} \right)\) là dãy số tăng và bị chặn.
Phương pháp:
• Chứng minh \(\left( {{u_n}} \right)\) là dãy số tăng:
Bước 1: Tìm \({u_{n + 1}}\).
Bước 2: Xét hiệu \({u_{n + 1}} - {u_n}\).
Bước 3: Chứng minh \({u_{n + 1}} - {u_n} > 0 \Leftrightarrow {u_{n + 1}} > {u_n},\forall n \in {\mathbb{N}^*}\), từ đó kết luận dãy số \(\left( {{u_n}} \right)\) là dãy số tăng.
• Chứng minh \(\left( {{u_n}} \right)\) bị chặn: Sử dụng tính chất của bất đẳng thức.
Lời giải:
• Ta có: \({u_{n + 1}} = \frac{{2\left( {n + 1} \right) - 1}}{{\left( {n + 1} \right) + 1}} = \frac{{2n + 2 - 1}}{{n + 1 + 1}} = \frac{{2n + 1}}{{n + 2}}\)
Xét hiệu:
\(\begin{array}{l}{u_{n + 1}} - {u_n} = \frac{{2n + 1}}{{n + 2}} - \frac{{2n - 1}}{{n + 1}} = \frac{{\left( {2n + 1} \right)\left( {n + 1} \right) - \left( {2n - 1} \right)\left( {n + 2} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\\ = \frac{{\left( {2{n^2} + n + 2n + 1} \right) - \left( {2{n^2} - n + 4n - 2} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\\ = \frac{{2{n^2} + n + 2n + 1 - 2{n^2} + n - 4n + 2}}{{\left( {n + 2} \right)\left( {n + 1} \right)}} = \frac{3}{{\left( {n + 2} \right)\left( {n + 1} \right)}} > 0,\forall n \in {\mathbb{N}^*}\end{array}\)
Vậy \({u_{n + 1}} - {u_n} > 0 \Leftrightarrow {u_{n + 1}} > {u_n}\). Vậy dãy số \(\left( {{u_n}} \right)\) là dãy số tăng.
• Ta có: \({u_n} = \frac{{2n - 1}}{{n + 1}} = \frac{{2\left( {n + 1} \right) - 3}}{{n + 1}} = 2 - \frac{3}{{n + 1}}\)
\(\forall n \in {\mathbb{N}^*}\) ta có:
\(n + 1 > 0 \Leftrightarrow \frac{3}{{n + 1}} > 0 \Leftrightarrow 2 - \frac{3}{{n + 1}} < 2 \Leftrightarrow {u_n} < 2\). Vậy \(\left( {{u_n}} \right)\) bị chặn trên.
\(n \ge 1 \Leftrightarrow n + 1 \ge 1 + 1 \Leftrightarrow n + 1 \ge 2 \Leftrightarrow \frac{3}{{n + 1}} \le \frac{3}{2} \Leftrightarrow 2 - \frac{3}{{n + 1}} \ge 2 - \frac{3}{2} \Leftrightarrow {u_n} \ge \frac{1}{2}\)
Vậy \(\left( {{u_n}} \right)\) bị chặn dưới.
Ta thấy dãy số \(\left( {{u_n}} \right)\) bị chặn trên và bị chặn dưới nên dãy số \(\left( {{u_n}} \right)\) bị chặn.
Bài 6 trang 50 SGK Toán 11 tập 1 - Chân trời sáng tạo
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{na + 2}}{{n + 1}}\). Tìm giá trị của \(a\) để:
a) \(\left( {{u_n}} \right)\) là dãy số tăng;
b) \(\left( {{u_n}} \right)\) là dãy số giảm.
Phương pháp:
Bước 1: Tìm \({u_{n + 1}}\).
Bước 2: Xét hiệu \({u_{n + 1}} - {u_n}\).
Bước 3:
– Để \(\left( {{u_n}} \right)\) là dãy số tăng thì ta tìm \(a\) sao cho \({u_{n + 1}} - {u_n} > 0,\forall n \in {\mathbb{N}^*}\).
– Để \(\left( {{u_n}} \right)\) là dãy số giảm thì ta tìm \(a\) sao cho \({u_{n + 1}} - {u_n} < 0,\forall n \in {\mathbb{N}^*}\).
Lời giải:

Vì n ∈ ℕ* nên (n + 1)(n + 2) > 0 nên dấu của hiệu un+1 – un phụ thuộc vào dấu của biểu thức a – 2.
a) Để (un) là dãy số tăng thì un+1 – un > 0 nên a – 2 > 0 ⇔ a > 2.
b) Để (un) là dãy số giảm thì un+1 – un < 0 nên a – 2 < 0 ⇔ a < 2.
Bài 7 trang 50 SGK Toán 11 tập 1 - Chân trời sáng tạo
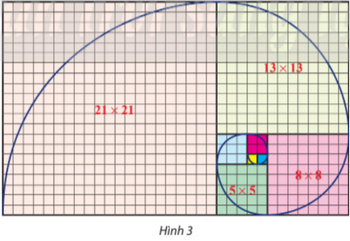
Trên lưới ô vuông, mỗi ô cạnh 1 đơn vị, người ta vẽ 8 hình vuông và tô màu khác nhau như Hình 3. Tìm dãy số biểu diễn độ dài cạnh của 8 hình vuông đỏ từ nhỏ đến lớn. Có nhận xét gì về dãy số trên?
Phương pháp:
Dựa vào hình vẽ, tìm độ dài cạnh của các hình vuông theo thứ tự từ nhỏ đến lớn.
Lời giải:
Ta có: \({u_1} = 1;{u_2} = 1;{u_3} = 2;{u_4} = 3;{u_5} = 5;{u_6} = 8;{u_7} = 13;{u_8} = 21\)
Ta có:
\(\begin{array}{l}{u_3} = 2 = {u_2} + {u_1}\\{u_4} = 3 = {u_3} + {u_2}\\{u_5} = 5 = {u_4} + {u_3}\\{u_6} = 8 = {u_5} + {u_4}\\{u_7} = 13 = {u_6} + {u_5}\\{u_8} = 21 = {u_7} + {u_6}\end{array}\)
Ta thấy dãy số này kể từ số hạng thứ 3 bằng tổng của hai số hạng đứng trước nó.
Vậy dãy số này có công thức truy hồi là:
\(\left\{ \begin{array}{l}{u_1} = 1;{u_2} = 1\\{u_n} = {u_{n - 1}} + {u_{n - 2}}\left( {n \ge 3} \right)\end{array} \right.\)
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài tập cuối chương 9
- Bài 2. Biến cố hợp và quy tắc cộng xác suất
- Bài 1. Biến cố giao và quy tắc nhân xác suất
- CHƯƠNG IX. XÁC SUẤT
- Bài tập cuối chương 8
- Bài 5. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
- Bài 4. Khoảng cách trong không gian
- Bài 3. Hai mặt phẳng vuông góc
- Bài 2. Đường thẳng vuông góc với mặt phẳng
- Bài 1. Hai đường thẳng vuông góc
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
