Giải SGK Toán 12 tập 1 Chân trời sáng tạo trang 64
Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 64 SGK Toán 12 Chân trời sáng tạo tập 1. Cho hình hộp ABCD.A′B′C′D′ có A(1; 0; 1), B(2; 1; 2), D(1; –1; 1), C′(4; 5; –5). Tìm toạ độ các đỉnh còn lại của hình hộp.
Bài 1 trang 64 SGK Toán 12 Tập 1 Chân trời sáng tạo
Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\), ta có biểu thức tọa độ của tích vô hướng \(\overrightarrow a .\overrightarrow b = {a_1}{b_1} + {a_2}{b_2} + {a_3}{b_3}\)
Lời giải:
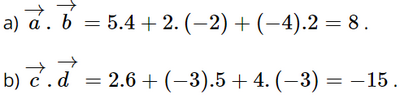
Bài 2 trang 64 SGK Toán 12 Tập 1 Chân trời sáng tạo
Cho hai vectơ \(\overrightarrow a \) = (0; 1; 3) và \(\overrightarrow b \) = (–2; 3; 1). Tìm toạ độ của vectơ \(2\overrightarrow b - \frac{3}{2}\overrightarrow a \)
Lời giải:
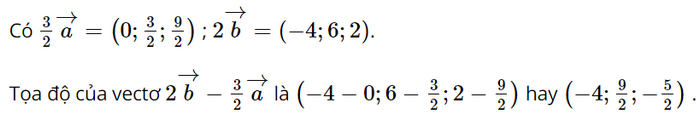
Bài 3 trang 64 SGK Toán 12 Tập 1 Chân trời sáng tạo
Cho ba điểm A(2; 1; –1), B(3; 2; 0) và C(2; –1; 3).
a) Chứng minh rằng A, B, C là ba đỉnh của một tam giác. Tính chu vi tam giác ABC.
b) Tìm toạ độ trung điểm của các cạnh của tam giác ABC.
c) Tìm toạ độ trọng tâm G của tam giác ABC.
Phương pháp:
a) A, B, C không thẳng hàng thì tạo thành một tam giác. Chu vi tam giác bằng tổng độ dài 3 cạnh
b) Cho tam giác ABC có \(A({a_1};{a_2};{a_3})\), \(B({b_1};{b_2};{b_3})\), \(C({c_1};{c_2};{c_3})\), ta có \(M(\frac{{{a_1} + {b_1}}}{2};\frac{{{a_2} + {b_2}}}{2};\frac{{{a_3} + {b_3}}}{2})\) là trung điểm của AB
c) \(G(\frac{{{a_1} + {b_1} + {c_1}}}{3};\frac{{{a_2} + {b_2} + {c_2}}}{3};\frac{{{a_3} + {b_3} + {c_3}}}{3})\) là trọng tâm của tam giác ABC
Lời giải:

Bài 4 trang 64 SGK Toán 12 Tập 1 Chân trời sáng tạo
Cho điểm M(1; 2; 3). Hãy tìm toạ độ của các điểm:
a) \({M_1},{M_2},{M_3}\) lần lượt là hình chiếu vuông góc của M trên các mặt phẳng toạ độ (Oxy), (Oyz), (Oxz).
b) M′, M″, M′′′ lần lượt là điểm đối xứng của M qua O, mặt phẳng (Oxy) và trục Oy.
Phương pháp:
a) Có \(A({a_1};{a_2};{a_3})\), tọa độ của hình chiếu của A lên (Oxy) là \(({a_1};{a_2};0)\), lên (Oyz) là \((0;{a_2};{a_3})\), lên (Oxz) là \(({a_1};0;{a_3})\)
b) Áp dụng công thức tìm tọa độ trung điểm
Lời giải:

Bài 5 trang 64 SGK Toán 12 Tập 1 Chân trời sáng tạo
Cho ba điểm A(3; 3; 3), B(1; 1; 2) và C(5; 3; 1).
a) Tìm điểm M trên trục Oy cách đều hai điểm B, C.
b) Tìm điểm N trên mặt phẳng (Oxy) cách đều ba điểm A, B, C.
Phương pháp:
Áp dụng công thức tính độ lớn vecto \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \)
Lời giải:
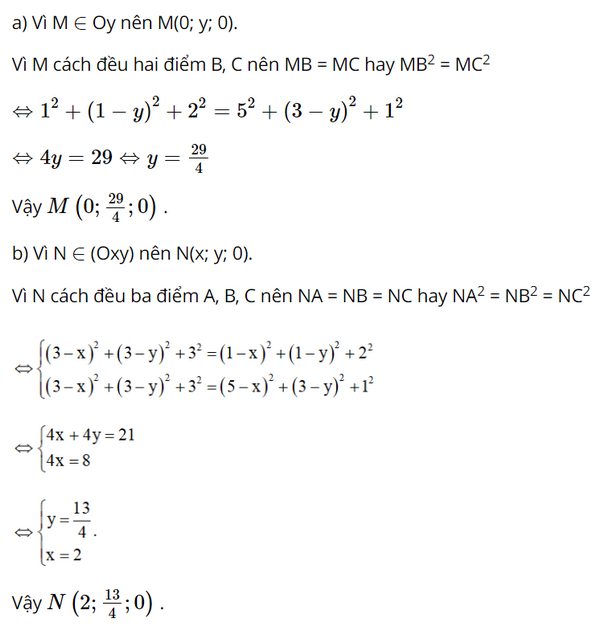
Bài 6 trang 64 SGK Toán 12 Tập 1 Chân trời sáng tạo
Cho các điểm A(–1; –1; 0), B(0; 3; –1), C(–1; 14; 0), D(–3; 6; 2). Chứng minh rằng ABCD là hình thang.
Phương pháp:
Chứng minh ABCD có một cặp cạnh đối song song thì ABCD là hình thang
Lời giải:

Bài 7 trang 64 SGK Toán 12 Tập 1 Chân trời sáng tạo
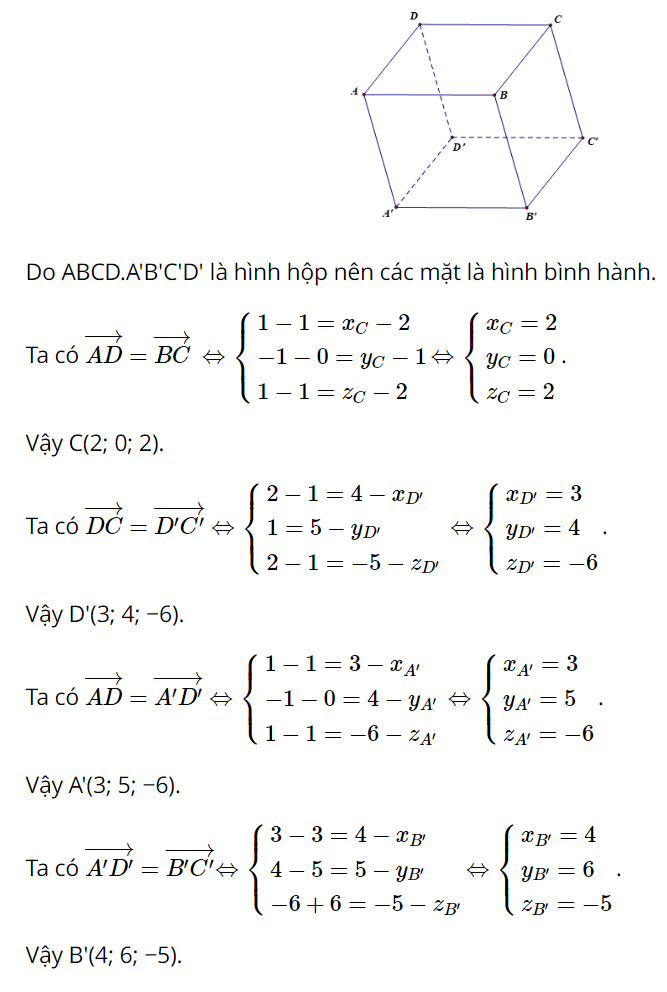
Cho hình hộp ABCD.A′B′C′D′ có A(1; 0; 1), B(2; 1; 2), D(1; –1; 1), C′(4; 5; –5). Tìm toạ độ các đỉnh còn lại của hình hộp.
Phương pháp:
Áp dụng tính chất 2 vecto bằng nhau
Lời giải:
Bài 8 trang 64 SGK Toán 12 Tập 1 Chân trời sáng tạo
Tính công sinh bởi lực \(\overrightarrow F \)= (20; 30; –10) (đơn vị: N) tạo bởi một drone giao hàng (Hình 7) khi thực hiện một độ dịch chuyển \(\overrightarrow d \)= (150; 200; 100) (đơn vị: m).

Phương pháp:
Áp dụng công thức tính công \(A = \overrightarrow F .\overrightarrow d \)
Lời giải:
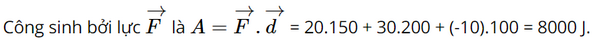
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải SGK Toán 12 tập 2 Chân trời sáng tạo trang 27 (29/07)
- Giải SGK Toán 12 tập 2 Chân trời sáng tạo trang 20 (29/07)
- Giải SGK Toán 12 tập 2 Chân trời sáng tạo trang 11, 12 (29/07)
- Giải SGK Toán 12 tập 1 Chân trời sáng tạo trang 92, 93 (29/07)
- Giải SGK Toán 12 tập 1 Chân trời sáng tạo trang 89 (29/07)
- Bài 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số bằng máy tính cầm tay
- Bài 1: Vẽ đồ thị hàm số bằng phần mềm Geogebra
- Hoạt động thực hành và trải nghiệm
- Bài tập cuối chương 3
- Bài 2: Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm
- Bài 1: Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm
- Chương 3: Các số đặc trưng đo mức độ phân tán cho mẫu số liệu ghép nhóm
- Bài tập cuối chương 2
- Bài 3: Biểu thức toạ độ của các phép toán vectơ
- Bài 2: Toạ độ của vectơ trong không gian
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
