Giải Toán 7 trang 14, 15 Chân trời sáng tạo tập 2
Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9 trang 14, 15 SGK Toán lớp 7 chân trời sáng tạo tập 2. Bài 8. Một tam giác có độ dài ba cạnh tỉ lệ với 3; 4; 5 và có chu vi là 60 cm. Tính độ dài các cạnh của tam giác đó.
Bài 1 trang 14 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho hai đại lượng a và b tỉ lệ thuận với nhau. Biết rằng khi a = 2 thì b = 18.
a) Tìm hệ số tỉ lệ k của a đối với b.
b) Tính giá trị của b khi a = 5.
Phương pháp:
a) Biểu diễn a theo b
b) Thay a = 5 vào công thức liên hệ giữa a và b, tìm b
Lời giải:
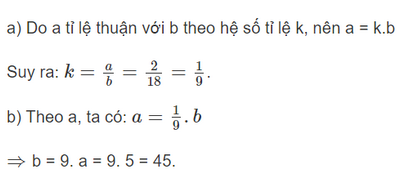
Bài 2 trang 14 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho hai đại lượng x và y tỉ lệ thuận với nhau. Biết rằng khi x = 7 thì y = 21.
a) Tìm hệ số tỉ lệ của y đối với x và biểu diễn y theo x
b) Tìm hệ số tỉ lệ của x đối với y và biểu diễn x theo y
Phương pháp:
Nếu x tỉ lệ thuận với y theo hệ số tỉ lệ k thì y tỉ lệ thuận với x theo hệ số tỉ lệ \(\dfrac{1}{k}\)
Lời giải:
a) Hệ số tỉ lệ của y đối với x là: k = 21 : 7 = 3.
Vậy ta có: y = 3. x
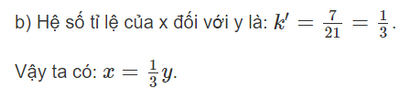
Bài 3 trang 14 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho m và n là hai đại lượng tỉ lệ thuận với nhau. Hãy viết công thức tính m theo n và tìm các giá trị chưa biết trong bảng sau:
|
n |
-2 |
-1 |
0 |
1 |
2 |
|
m |
? |
? |
? |
-5 |
? |
Phương pháp:
Biểu diễn m theo n.
Thay giá trị của n vào công thức để tìm m tương ứng.
Lời giải:
Vì n = 1, m = -5, mà m và n là 2 đại lượng tỉ lệ thuận nên ta có: hệ số tỉ lệ của m đối với n là: k = (-5) : 1 = -5
Từ đó ta có mối liên hệ: m = -5.n
| n | -2 | -1 | 0 | 1 | 2 |
| m | 10 | 5 | 0 | -5 | -10 |
Bài 4 trang 14 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho biết hai đại lượng S và t tỉ lệ thuận với nhau:
|
S |
1 |
2 |
3 |
4 |
5 |
|
t |
-3 |
? |
? |
? |
? |
a) Tính các giá trị chưa biết trong bảng trên
b) Viết công thức tính t theo S
Phương pháp:
Áp dụng tính chất của đại lượng tỉ lệ thuận:\(\dfrac{S_1}{t_1}=\dfrac{S_2}{t_2}=\dfrac{S_3}{t_3}=...\)
Lời giải:
a)
| S | 1 | 2 | 3 | 4 | 5 |
| t | -3 | -6 | -9 | -12 | -15 |
b) Hệ số tỉ lệ của t đối với S là: k = (-3) : 1 = -3
Vậy ta có: t = (-3).S
Bài 5 trang 14 SGK Toán 7 tập 2 - Chân trời sáng tạo
Trong các trường hợp sau, hãy kiểm tra đại lượng x có tỉ lệ thuận với đại lượng y hay không:
a)
|
x |
2 |
4 |
6 |
-8 |
|
y |
1,2 |
2,4 |
3,6 |
- 4,8 |
b)
|
x |
1 |
2 |
3 |
4 |
5 |
|
y |
3 |
6 |
9 |
12 |
25 |
Phương pháp:
Kiểm tra các tỉ lệ x và y tương ứng.
+ Nếu các tỉ lệ bằng nhau thì 2 đại lượng x và y tỉ lệ thuận.
+ Nếu có tỉ lệ không bằng nhau thì 2 đại lượng x và y không tỉ lệ thuận.
Lời giải:
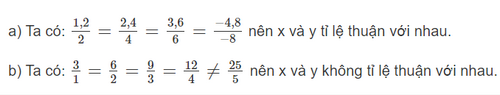
Bài 6 trang 15 SGK Toán 7 tập 2 - Chân trời sáng tạo
Hai chiếc nhẫn bằng kim loại đồng chất có thể tích là \(3c{m^3}\) và \(2c{m^3}\). Hỏi mỗi chiếc nhẫn nặng bao nhiêu gam, biết rằng hai chiếc nhẫn nặng 96,5 g? (Cho biết khối lượng và thể tích là hai đại lượng ti lệ thuận với nhau)
Phương pháp:
Áp dụng tính chất của dãy tỉ số bằng nhau: \(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+c}{b+d}\)
Lời giải:

Bài 7 trang 15 SGK Toán 7 tập 2 - Chân trời sáng tạo
Bốn cuộn dây điện cùng loại có tổng khối lượng là 26 kg.
a) Tính khối lượng từng cuộn, biết cuộn thứ nhất nặng bằng \(\dfrac{1}{2}\) cuộn thứ hai , bằng \(\dfrac{1}{4}\)cuộn thứ ba và bằng \(\dfrac{1}{6}\) cuộn thứ tư.
b) Biết cuộn thứ nhất dài 100m, hãy tính xem một mét dây điện nặng bao nhiêu gam.
Phương pháp:
Gọi khối lượng cuộn 1 là x và biểu diễn khối lượng các cuộn còn lại theo x
Lời giải:
a) Gọi khối lượng cuộn dây thứ nhất, thứ hai, thứ ba và thứ tư lần lượt là: a, b, c, d. (a, b, c, d > 0).
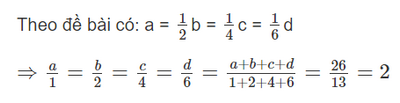
⇒ a = 2; b = 2. 2 = 4; c = 2. 4 = 8; d = 2. 6 = 12
Vậy khối lượng các cuộn dây thứ nhất, thứ hai, thứ ba, thứ tư lần lượt là: 2 kg; 4kg; 8 kg và 12 kg.
b) Cuộn dây thứ nhất nặng 2 kg tương ứng dài 100m. Nên một mét dây điện nặng: 2 : 100 = 0,02 kg = 20 g.
Bài 8 trang 15 SGK Toán 7 tập 2 - Chân trời sáng tạo
Một tam giác có độ dài ba cạnh tỉ lệ với 3; 4; 5 và có chu vi là 60 cm. Tính độ dài các cạnh của tam giác đó.
Phương pháp:
Sử dụng tính chất của dãy tỉ số bằng nhau: \(\dfrac{a}{b} = \dfrac{c}{d}=\dfrac{e}{f} = \dfrac{{a +c+e}}{{b +d+f}}\)
Lời giải:
Gọi độ dài 3 cạnh của tam giác lần lượt là: a, b, c. (a,b,c>0).
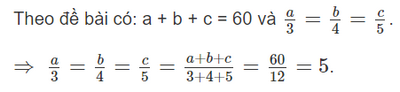
⇒ a = 5. 3 =15; b = 5.4 = 20; c = 5.5 = 25.
Vậy độ dài ba cạnh của tam giác là: 15 cm, 20 cm, 25 cm.
Bài 9 trang 15 SGK Toán 7 tập 2 - Chân trời sáng tạo
Tiến, Hùng và Mạnh cùng đi câu cá trong dịp hè. Tiến câu được 12 con, Hùng câu được 8 con và Mạnh câu được 10 con. Số tiền bán cá thu được tổng cộng là 180 nghìn đồng. Hỏi nếu đem số tiền trên chia cho các bạn theo tỉ lệ với số cá từng người câu được thì mỗi bạn nhận được bao nhiêu tiền?
Phương pháp:
Sử dụng tính chất của dãy tỉ số bằng nhau: \(\dfrac{a}{b} = \dfrac{c}{d}=\dfrac{e}{f} = \dfrac{{a+c+e}}{{b+d+f}}\)
Lời giải:
Gọi số tiền 3 bạn Tiến, Hùng, Mạnh câu được lần lượt là T,H,M ( nghìn đồng) (T,H,M > 0)
Theo đề bài 3 bạn bán tổng cộng được 180 nghìn nên ta có :
T + H + M = 180
Đem số tiền chia cho các bạn tỉ lệ với số cá từng người câu được, ta sẽ có : \(\dfrac{T}{{12}} = \dfrac{H}{8} = \dfrac{M}{{10}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{T}{{12}}=\dfrac{H}{8} = \dfrac{M}{{10}} = \dfrac{{T + H + M}}{{12 + 8 + 10}} = \dfrac{{180}}{{30}}= 6\)
\( \Rightarrow T = 6.12=72; H=6.8=48;M=6.10=60\)
Vậy số tiền Tiến, Hùng, Mạnh bán được lần lượt là : 72 nghìn, 48 nghìn và 60 nghìn đồng.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài tập cuối chương 9 - CTST
- Bài 2. Làm quen với xác suất của biến cố ngẫu nhiên - CTST
- Bài 1. Làm quen với biến cố ngẫu nhiên - CTST
- Chương 9. Một số yếu tố xác suất - CTST
- Bài tập cuối chương 8 - CTST
- Bài 9. Tính chất ba đường phân giác của tam giác - CTST
- Bài 8. Tính chất ba đường cao của tam giác
- Bài 7. Tính chất ba đường trung tuyến của tam giác - CTST
- Bài 6. Tính chất ba đường trung trực của tam giác - CTST
- Bài 5. Đường trung trực của một đoạn thẳng - CTST
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
