Giải Toán 7 trang 18 Kết nối tri thức với cuộc sống tập 2

Bài 6.22 trang 18 SGK Toán 7 tập 2 - Kết nối tri thức

Cho biết x, y là hai đại lượng tỉ lệ nghịch. Thay mỗi dấu “?” trong bảng sau bằng số thích hợp.

Viết công thức mô tả mối quan hệ phụ thuộc giữa hai đại lượng x và y.

Phương pháp:

Sử dụng tính chất của hai đại lượng tỉ lệ nghịch: x₁y₁ = x₂y₂=….

Lời giải:

Bài 6.23 trang 18 SGK Toán 7 tập 2 - Kết nối tri thức

Theo bảng giá trị dưới đây, hai đại lượng x và y có phải là hai đại lượng tỉ lệ nghịch không?

Phương pháp:

Kiểm tra tích 2 giá trị tương ứng của chúng có luôn bằng nhau không.

+ Nếu bằng thì 2 đại lượng đó tỉ lệ nghịch

+ Nếu không bằng thì 2 đại lượng đó không là hai đại lượng tỉ lệ nghịch

Lời giải:

Hai đại lượng x và y ở bảng giá trị không phải là hai đại lượng tỉ lệ nghịch.

Bài 6.24 trang 18 SGK Toán 7 tập 2 - Kết nối tri thức

Cho biết y tỉ lệ nghịch với x theo hệ số tỉ lệ a, x tỉ lệ nghịch với z theo hệ số tỉ lệ b. Hỏi y tỉ lệ thuận hay tỉ lệ nghịch với z và hệ số tỉ lệ là bao nhiêu?

Phương pháp:

+ Sử dụng định nghĩa 2 đại lượng tỉ lệ thuận và tỉ lệ nghịch:

Nếu y = a.x (a là hằng số khác 0) thì y tỉ lệ thuận với x theo hệ số tỉ lệ a.

Nếu \(y = \dfrac{a}{x}\)(a là hằng số khác 0) thì y tỉ lệ nghịch với x theo hệ số tỉ lệ a

+ Biểu diễn đại lượng y theo z.

Nếu y = k. z ( k là hằng số) thì y và z là hai đại lượng tỉ lệ thuận.

Nếu \(y = \dfrac{k}{z}\) ( k là hằng số) thì y và z là hai đại lượng tỉ lệ nghịch.

Vì y tỉ lệ nghịch với x theo hệ số tỉ lệ a nên y = \(\dfrac{a}{x}\)

Vì x tỉ lệ nghịch với z theo hệ số tỉ lệ b nên x = \(\dfrac{b}{z}\)

Do đó, \(y = \dfrac{a}{x} = \dfrac{a}{{\dfrac{b}{z}}} = a:\dfrac{b}{z} = a.\dfrac{z}{b} = \dfrac{a}{b}.z\) ( \(\dfrac{a}{b}\) là hằng số vì a,b là các hằng số)

Vậy y có tỉ lệ thuận với z và hệ số tỉ lệ là \(\dfrac{a}{b}\)

Lời giải:

y tỉ lệ nghịch với x theo hệ số tỉ lệ a => 

  x tỉ lệ nghịch với z theo hệ số tỉ lệ b => 

=> y tỉ lệ nghịch với z.

* Công thức: 

Ta có: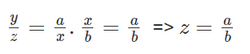 

* Vậy: y tỉ lệ thuận với z theo hệ số tỉ lệ là 

Bài 6.25 trang 18 SGK Toán 7 tập 2 - Kết nối tri thức

Với cùng số tiền để mua 17 tập giấy A4 loại 1 có thể mua bao nhiêu tập giấy A4 loại 2, biết rằng giá tiền giấy loại 2 chỉ bằng 85% giá tiền giấy loại 1.

Phương pháp:

Số tập giấy mua được và giá tiền tương ứng là hai đại lượng tỉ lệ nghịch.

Áp dụng tính chất của hai đại lượng tỉ lệ thuận :\(\dfrac{{{x_1}}}{{{x_2}}} = \dfrac{{{y_2}}}{{{y_1}}}\)

Lời giải:

Gọi x (số tập giấy) là số tập giấy A4 loại 2.

- Giả sử số tiền mua 17 tập giấy A4 loại 1 là a.

Mà giá tiền giấy loại 2 chỉ bằng 85% nên giá mua là 0,85a.

- Vì số tiền mua tập giấy không đổi nên số tiền và số tập giấy là hai đại lượng tỉ lệ nghịch.

- Theo tính chất của 2 đại lượng tỉ lệ nghịch, ta có:

17a = 0,85ax => 

* Vậy: số tập giấy A4 loại 2 có thể mua là 20 tập giấy.

Bài 6.26 trang 18 SGK Toán 7 tập 2 - Kết nối tri thức

Ba đội máy cày làm trên ba cánh đồng cùng diện tích. Đội thứ nhất hoàn thành công việc trong 4 ngày, đội thứ hai trong 6 ngày và đội thứ ba trong 8 ngày. Hỏi mỗi đội có mấy máy cày, biết rằng số máy cày của đội thứ nhất nhiều hơn số máy cày của đội thứ hai là 2 máy và năng suất của các máy như nhau?

Phương pháp:

Gọi số máy mỗi đội lần lượt là x,y,z (máy) (x,y,z \( \in \)N*).

Số máy cày và thời gian hoàn thành là 2 đại lượng tỉ lệ nghịch

Sử dụng tính chất của dãy tỉ số bằng nhau: \(\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{e}{f} = \dfrac{{a - c}}{{b - d}}\)

Lời giải:

Gọi x, y và z lần lượt là số máy cày ở mỗi đội thứ nhất, thứ hai và thứ ba.

Theo đề bài, ta có: x–y=2

- Vì năng suất của các máy như nhau, nên ta có: 

4x = 6y = 8z hay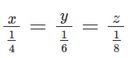  

- Theo tính chất của dãy tỉ số bằng nhau, ta có:

=> Suy ra: 

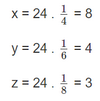
* Vậy:  

• Số máy cày ở đội thứ nhất là 8 máy.
• Số máy cày ở đội thứ hai là 4 máy.
• Số máy cày ở đội thứ ba là 3 máy.

Sachbaitap.com