Giải Toán 7 trang 46, 47 Chân trời sáng tạo tập 2
Giải bài 1, 2, 3, 4, 5, 6 trang 46, 47 SGK Toán lớp 7 chân trời sáng tạo tập 2. Bài 5. Cho tam giác ABC có BC = 1cm, AB = 4cm. Tìm độ dài cạnh AC, biết rằng độ dài này là một số nguyên xăngtimét.
Bài 1 trang 46 SGK Toán 7 tập 2 - Chân trời sáng tạo
Tìm số đo các góc chưa biết của các tam giác trong Hình 5.
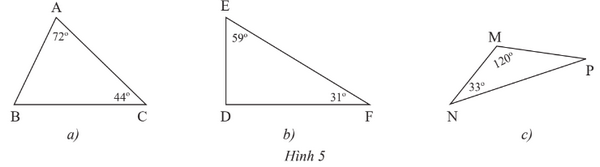
Phương pháp:
Sử dụng định lí về tổng các góc trong tam giác
Lời giải:
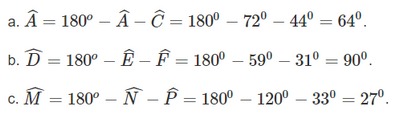
Bài 2 trang 47 SGK Toán 7 tập 2 - Chân trời sáng tạo
Tính số đo x của góc trong Hình 6.
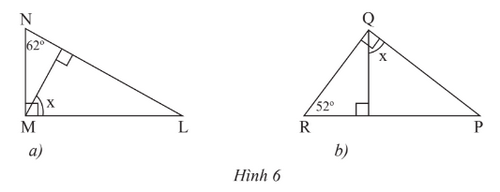
Phương pháp:
Sử dụng định lí tổng 3 góc trong tam giác
Lời giải:

Bài 3 trang 47 SGK Toán 7 tập 2 - Chân trời sáng tạo
Hãy chia tứ giác ABCD trong Hình 7 thành hai tam giác để tính tổng số đo của bốn góc \(\widehat A\),\(\widehat B\),\(\widehat C\),\(\widehat D\).
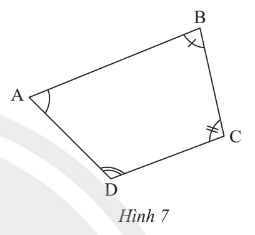
Phương pháp:
Ta chia tứ giác thành 2 tam giác
Áp dụng định lí tổng ba góc trong một tam giác
Lời giải:
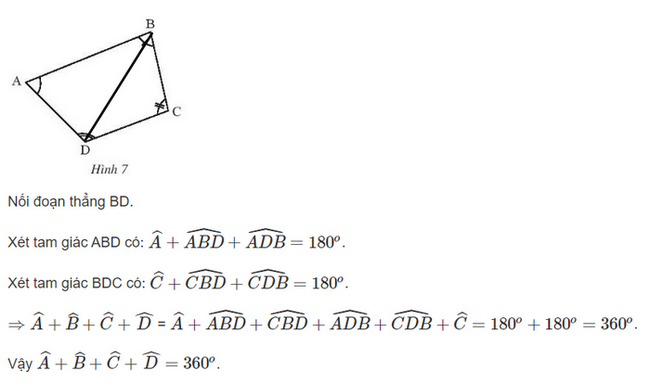
Bài 4 trang 47 SGK Toán 7 tập 2 - Chân trời sáng tạo
Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của tam giác?
a) 4cm; 5cm; 7cm
b) 2cm; 4cm; 6cm
c) 3cm; 4cm; 8cm
Phương pháp:
Khi kiểm tra 3 đoạn thẳng có thỏa mãn bất đẳng thức tam giác không, để nhanh gọn, ta chỉ cần kiểm tra tổng độ dài của 2 cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất hay không
Lời giải:
a) 5 - 4 < 7 < 4 + 5.
b) 2+ 4 = 6.
c) 3 + 4 < 8.
Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba câu a) 4cm, 5cm, 7cm có thể là độ dài ba cạnh của một tam giác.
Bài 5 trang 47 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho tam giác ABC có BC = 1cm, AB = 4cm. Tìm độ dài cạnh AC, biết rằng độ dài này là một số nguyên xăngtimét.
Phương pháp:
Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại và lớn hơn hiệu độ dài 2 cạnh còn lại: b – c < a < b + c ( với a, b, c là độ dài 3 cạnh của tam giác)
Kết hợp điều kiện độ dài cạnh CA là số nguyên
Lời giải:
Áp dụng đính lí về độ dài 3 cạnh của một tam giác ta có: 4 - 1 < AC < 4 + 1, hay 3 < AC < 5.
Vì độ đài AC là một số nguyên, nên độ dài AC có thể là: 4.
Thử lại giá trị vừa tìm được 5 < 3 + 4 thỏa mãn định lí.
Vậy độ dài AC = 4cm.
Bài 6 trang 47 SGK Toán 7 tập 2 - Chân trời sáng tạo
Trong một trường học, người ta bắt đầu đánh dấu ba khu vực A, B, C là ba đỉnh của một tam giác, biết các khoảng cách AC = 15m, AB = 45m
a) Nếu đặt ở khu vực C một thiết bị phát wifi có bán kính hoạt động 30m thì tại khu vực B có nhận được tín hiệu không? Vì sao?
b) Cũng câu hỏi như trên với thiết bị phát wifi có bán kính hoạt động 60m.
Phương pháp:
Ta áp dụng bất đẳng thức tam giác:
AB - AC < BC < AB + AC
Lời giải:
Áp dụng định lí về độ dài 3 cạnh của một tam giác có: 45 - 15 < BC < 45 + 15, hay 30 < BC < 60.
a) Nếu đặt ở khu vực C một thiết bị phát wifi có bán kính hoạt động 30 m thì khu vực B không nhận được tín hiệu vì BC > 30 m.
b) Nếu đặt ở C một thiết bị phát wifi có bán kính hoạt động 60 m thì khu vực B nhận được tín hiệu vì BC < 60 m.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài tập cuối chương 9 - CTST
- Bài 2. Làm quen với xác suất của biến cố ngẫu nhiên - CTST
- Bài 1. Làm quen với biến cố ngẫu nhiên - CTST
- Chương 9. Một số yếu tố xác suất - CTST
- Bài tập cuối chương 8 - CTST
- Bài 9. Tính chất ba đường phân giác của tam giác - CTST
- Bài 8. Tính chất ba đường cao của tam giác
- Bài 7. Tính chất ba đường trung tuyến của tam giác - CTST
- Bài 6. Tính chất ba đường trung trực của tam giác - CTST
- Bài 5. Đường trung trực của một đoạn thẳng - CTST
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
