Giải Toán 7 trang 62, 63 Chân trời sáng tạo tập 2

Bài 1 trang 62 SGK Toán 7 tập 2 - Chân trời sáng tạo

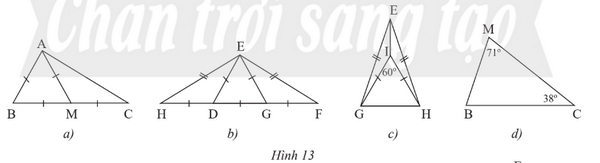
Tìm các tam giác cân và tam giác đều trong mỗi hình sau (Hình 13). Giải thích.

Phương pháp:

Dựa vào các cạnh bên và số đo các góc ở đáy mỗi tam giác

Lời giải:

a. ΔABM đều vì AB = AM = BM

ΔAMC cân tại M vì AM= MC

b. ΔEHF cân tại E vì EH = EF

ΔEDG đều vì: ED = EG = DG

ΔEDH cân tại D vì DE = DH

ΔEGF cân tại G vì GE = GF

c. ΔEGH cân tại E vì EG = EH

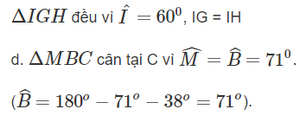
Bài 2 trang 62 SGK Toán 7 tập 2 - Chân trời sáng tạo

Cho Hình 14, biết ED = EF và EI là tia phân giác của \(\widehat {DEF}\)

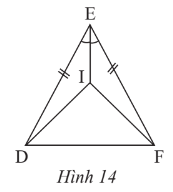
Chứng minh rằng:

a) \(\Delta EID = \Delta EIF\)

b) Tam giác DIF cân

Phương pháp:

- Ta sử dụng tính chất c-g-c để chứng minh câu a

- Từ câu a ta suy ra ID = FI và chứng minh được tam giác DIF cân

Lời giải:

a. Xét ΔEID và ΔEIF có:

EI chung

DE = EF.

⇒ ΔEID = ΔEIF (c.g.c)

b. Vì ΔEID=ΔEIF (chứng minh trên)

⇒ ID = IF

⇒ Tam giác DIF cân tại I.

Bài 3 trang 63 SGK Toán 7 tập 2 - Chân trời sáng tạo

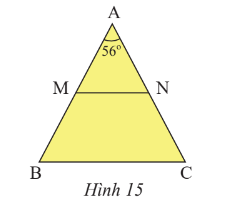
Cho tam giác ABC cân tại A có \(\widehat A = {56^o}\)(Hình 15)

a) Tính\(\widehat B\), \(\widehat C\)

b) Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh rằng tam giác AMN cân.

c) Chứng minh rằng MN // BC

Phương pháp:

a) Sử dụng định lí tổng 3 góc trong tam giác và tính chất 2 góc đáy tam giác cân

b) Chứng minh AM = AN

c) Sử dụng tính chất góc đồng vị

Lời giải:

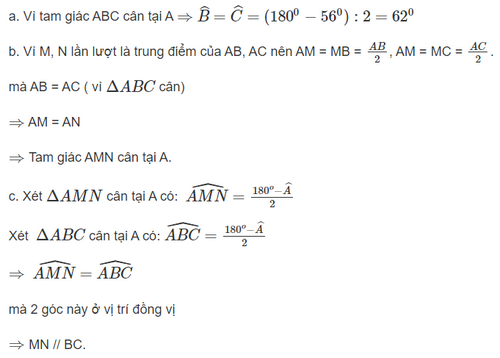
Bài 4 trang 63 SGK Toán 7 tập 2 - Chân trời sáng tạo

Cho tam giác ABC cân tại A (Hình 16). Tia phân giác của góc B cắt AC tại F, tia phân giác của góc C cắt AB tại E.

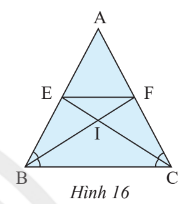
a) Chứng minh rẳng \(\widehat {ABF} = \widehat {ACE}\)

b) Chứng minh rằng tam giác AEF cân

c) Gọi I là giao điểm của BF và CE. Chứng minh rằng tam giác IBC và tam giác IEF là những tam giác cân

Phương pháp:

a) Sử dụng tính chất của tam giác cân và tia phân giác 

b) Từ câu a suy ra AE = AF

c) Tam giác IEF chứng minh cân bằng cách chứng minh 2 cạnh bên bằng nhau

Chứng minh IBC cân vì 2 góc đáy bằng nhau

Lời giải:

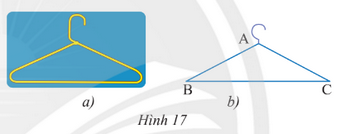
Bài 5 trang 63 SGK Toán 7 tập 2 - Chân trời sáng tạo

Phần thân của một móc treo quần áo có dạng hình tam giác cân (Hình 17a) được vẽ lại như Hình 17b. Cho biết AB = 20 cm; BC = 28 cm và \(\widehat B\)= 35°. Tìm số đo các góc còn lại và chu vi của tam giác ABC.

Phương pháp:

Áp dụng tính chất tam giác cân để tìm các góc, cạnh còn lại

Lời giải:

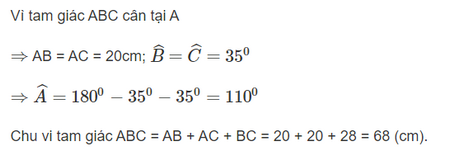
Bài 6 trang 63 SGK Toán 7 tập 2 - Chân trời sáng tạo

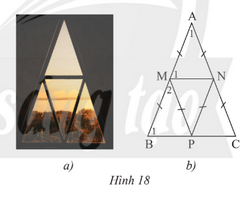
Một khung cửa sổ hình tam giác có thiết kế như Hình 18a được vẽ lại như Hình 18b.

a) Cho biết \(\widehat {{A_1}}\)\( = {42^o}\). Tính số đo của \(\widehat {{M_1}}\),\(\widehat {{B_1}}\),\(\widehat {{M_2}}\).

b) Chứng minh MN // BC, MP // AC.

c) Chứng minh bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau.

Phương pháp:

Sử dụng các tính chất của tam giác cân

Lời giải:

Sachbaitap.com