Giải Toán 7 trang 75, 76 Chân trời sáng tạo tập 2

Bài 1 trang 75 SGK Toán 7 tập 2 - Chân trời sáng tạo

Quan sát Hình 8.

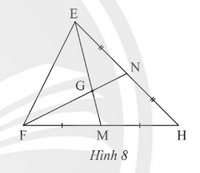
Tìm số thích hợp để ghi vào chỗ chấm trong các đẳng thức sau:

\(\begin{array}{l}EG = ...EM;\,\,\,GM = ...EM;\,\,\,\,GM = ...EG\\FG = ...GN;\,\,\,\,\,FN = ...GN;\,\,\,\,\,FN = ...FG\end{array}\)

Phương pháp:

Ta dựa vào định lí ba đường trung tuyến cắt nhau tại 1 điểm. Điểm đó cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\) độ dài trung tuyến đi qua đỉnh ấy .

Lời giải:

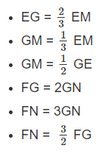
Bài 2 trang 75 SGK Toán 7 tập 2 - Chân trời sáng tạo

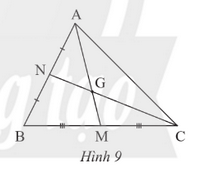
Quan sát Hình 9

a) Biết AM = 15 cm, tính AG

b) Biết GN = 6 cm, tính CN

Phương pháp:

- Ta dựa vào định lí ba đường trung tuyến cắt nhau tại 1 điểm. Điểm đó cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\)độ dài trung tuyến đi qua đỉnh ấy

- Ta áp dụng các tỉ lệ giữa các đoạn thẳng và độ dài của chúng

Lời giải:

Bài 3 trang 75 SGK Toán 7 tập 2 - Chân trời sáng tạo

Cho tam giác ABC. Hai đường trung tuyến AM và CN cắt nhau tại G. Trên tia đối của tia AM lấy điểm E sao cho ME = MG.

a) Chứng minh rằng BG song song với EC.

b) Gọi I là trung điểm của BE, AI cắt BG tại F. Chứng minh rằng AF = 2FI

Phương pháp:

- Ta dựa vào định lí ba đường trung tuyến cắt nhau tại 1 điểm. Điểm đó cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\)độ dài trung tuyến đi qua đỉnh ấy

- Câu a ta sẽ chứng minh 2 góc so le trong bằng nhau thông qua các tam giác bằng nhau

- Câu b ta sẽ chứng minh F là trọng tâm tam giác ABE

Lời giải:

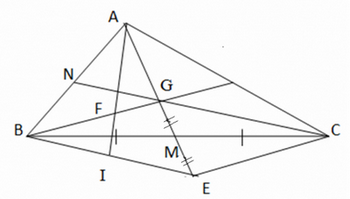
a) Xét  ∆BMG và  ∆CME ta có:

BM = CM (M là trung điểm của BC)

ME = MG (giả thiết)

=> ∆ BMG = ∆ CME (c.g.c)

Mà hai góc ở vị trị so le trong

=> GB // CE.

b) Xét tam giác ABC có AM và CN là hai đường trung tuyến cắt nhau tại G

=> G là trọng tâm của tam giác ABC

=> AG = 2GM

+ Ta có: GE = GM + EM

=> GE = 2GM (GM = EM)

=> AG = GE

=> G là trung điểm đoạn thẳng AE

=> BG là đường trung tuyến của tam giác ABM.

+ Xét tam giác ABM có: AI và BG là 2 đường trung tuyến

mà AI cắt BG tại F

=> F là trọng tâm của tam giác ABC

=> AF = 2FI.

Bài 4 trang 75 SGK Toán 7 tập 2 - Chân trời sáng tạo

Cho tam giác ABC cân tại A có BM và CN là hai đường trung tuyến.

a) Chứng minh rằng BM = CN

b) Gọi I là giao điểm của BM và CN, đường thẳng AI cắt BC tại H. Chứng minh H là trung điểm của BC

Phương pháp:

- Ta chứng minh 2 tam giác bằng nhau để từ đó chứng minh 2 đoạn thẳng bằng nhau

- Ta chứng minh I là trọng tâm tam giác ABC và chứng minh AH là trung tuyến của tam giác ABC và H là trung điểm của BC

Lời giải:

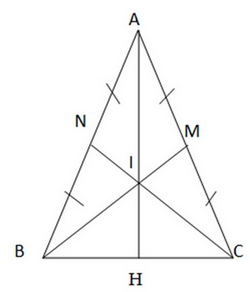
a) ∆ ABC cân tại A 

=> AB = AC  

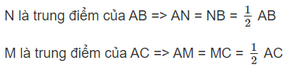
=> AN = AM

Xét ∆ ANC và ∆ AMB ta có:

AB = AC

AN = AM 

=>  ∆ ANC = ∆ AMB (c.g.c)

=> NC = MB 

b) 2 đường trung tuyến BM và CN cắt nhau tại I

=> I là trọng tâm của ∆ ABC

mà BM = CN

=> IB = IC

+ Xét ∆ ACI và ∆ ABI có : 

AB = AC

AI chung

IB = IC

=> ∆ ACI = ∆ ABI (c.c.c)

+ Xét ∆ ABH và ∆ ACH có : 

AB = AC

AH chung

=> ∆ ABH = ∆ ACH (c.g.c).

=> BH = CH

=> H là trung điểm của BC.

Bài 5 trang 76 SGK Toán 7 tập 2 - Chân trời sáng tạo

Cho tam giác ABC có đường trung tuyến BM bằng đường trung tuyến CN. Chứng minh rằng tam giác ABC cân.

Phương pháp:

- Ta chứng minh AB = AC bằng cách chứng minh 2 tam giác bằng nhau

Lời giải:

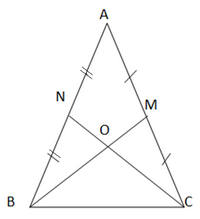
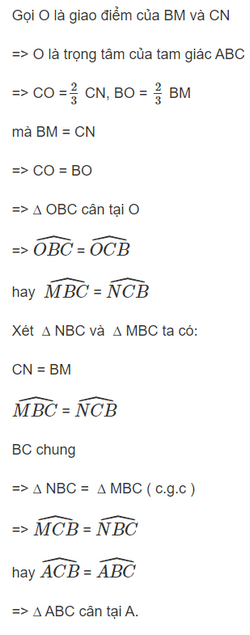
Bài 6 trang 76 SGK Toán 7 tập 2 - Chân trời sáng tạo

Cho tam giác ABC cân tại A có BD và CE là hai đường trung tuyến cắt nhau tại F (Hình 10). Biết BE = 9 cm, tính độ dài đoạn thẳng DF.

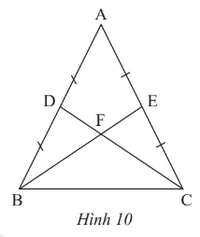
Phương pháp:

- Ta chứng minh F là trọng tâm tam giác ABC

- Sau đó chứng minh CD = BE

- Áp dụng định lí về trọng tâm tam giác ta tính các đoạn DF, EF

Lời giải:

+ ∆ ABC cân tại A

=> AB = AC

=> AD = AE

+ Xét ∆ ABE và ∆ ACD có : 

AB = AC 

AE = AD

=> ∆ ABE = ∆ ACD ( c.g.c)

=> BE = CD = 9 cm

+ Xét  ∆ ABC có hai đường trung tuyến BE và CD cắt nhau tại F

=> F là trọng tâm của tam giác ABC

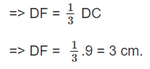
Sachbaitap.com