Bài 1, 2, 3, 4 trang 8 SGK Toán lớp 5 - Phân số thập phân

Bài 1 trang 8 SGK Toán lớp 5

Câu hỏi:

Đọc các phân số thập phân: 

\(\dfrac{9}{10}\);        \( \dfrac{21}{100}\);      \( \dfrac{625}{1000}\);       \( \dfrac{2005}{1000000}\).

Phương pháp:

Để đọc phân số, ta đọc tử số, đọc "phần" rồi sau đó đọc mẫu số.

Lời giải:

Chín phần mười;

Hai mươi mốt phần trăm;

Sáu trăm hai mươi lăm phần nghìn;

Hai nghìn không trăm linh năm phần triệu.

Bài 2 trang 8 SGK Toán lớp 5

Câu hỏi:

Viết các phân số thập phân:

Bảy phần mười;   hai mươi phần trăm;  bốn trăm bảy mươi lăm phần nghìn;  một phần triệu.

Lời giải:

Bảy phần mười: \( \dfrac{7}{10}\); 

Hai mươi phần trăm: \( \dfrac{20}{100}\) ;

Bốn trăm bảy mươi lăm phần nghìn: \( \dfrac{475}{1000}\);

Một phần triệu: \( \dfrac{1}{1000000}\).

Bài 3 trang 8 SGK Toán lớp 5

Câu hỏi:

Phân số nào dưới đây là phân số thập phân?

\( \dfrac{3}{7}\) ;  \( \dfrac{4}{10}\) ;  \( \dfrac{100}{34}\) ;  \( \dfrac{17}{1000}\) ;  \( \dfrac{69}{2000}\).

Lời giải:

Phân số thập phân là các phân số có mẫu số là \(10; 100; 1000; ...\)

Các phân số thập phân là: \( \dfrac{4}{10}\) ;  \( \dfrac{17}{1000}\).

Bài 4 trang 8 SGK Toán lớp 5

Câu hỏi:

Viết số thích hợp vào ô trống :

a) \( \dfrac{7}{2}=\dfrac{7 \times \square }{2\times\square }=\dfrac{\square }{10}\) ;

b) \( \dfrac{3}{4}=\dfrac{3\times \square }{4\times \square }=\dfrac{\square }{100}\) ;

c) \( \dfrac{6}{30}=\dfrac{6:\square }{30:\square }=\dfrac{\square }{10}\) ;

d) \( \dfrac{64}{800}=\dfrac{64:\square }{800:\square }=\dfrac{\square }{100}\) .

Phương pháp:

Áp dụng tính chất cơ bản của phân số:

- Nếu nhân cả tử và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.

- Nếu chia hết cả tử số và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.

Lời giải:

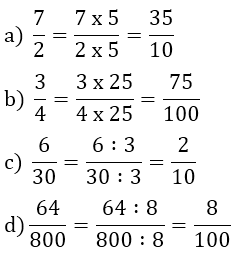
Sachbaitap.com