Câu 5.2 trang 91 Sách bài tập (SBT) Toán 8 tập 2

Cho tam giác ba góc nhọn ABC và một điểm O bất kì trong tam giác đó.

Ba điểm D, E, F theo thứ tự là trung điểm các cạnh AB, BC và CA. Ba điểm M, P, Q theo thứ tự là trung điểm của các đoạn thẳng OA, OB và OC.

a. Các tam giác DEF và MPQ có đồng dạng với nhau không ? Vì sao ? Tỉ số đồng dạng bằng bao nhiêu ?

Hãy sắp xếp các đỉnh tương ứng nếu hai tam giác đó đồng dạng.

b. Khi nào thì lục giác DPEQFM có tất cả các cạnh bằng nhau ? Hãy vẽ hình trong trường hợp đó.

Giải:

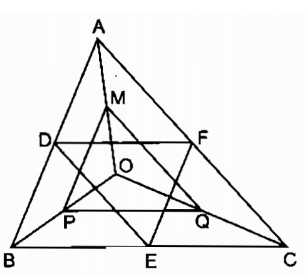
a. Theo giả thiết D, E, F lần lượt là trung điểm các cạnh AB, BC và CA nên DE, EF, FD là các đường trung bình của tam giác ABC. Do đó, ta có:

\(DE = {1 \over 2}AC,EF = {1 \over 2}AB,FD = {1 \over 2}BC\)            (1)

Mặt khác, M là trung điểm của OA, P là trung điểm của OB, Q là trung điểm của OC, xét các tam giác OAB, OBC, OCA, ta cũng có:

\(MP = {1 \over 2}AB,PQ = {1 \over 2}BC,QM = {1 \over 2}AC.\)                (2)

Từ đẳng thức (1) và (2), ta suy ra :

DE = QM, EF = MP, FD = PQ.

Do đó ta có: \({{DE} \over {QM}} = {{EF} \over {MP}} = {{FD} \over {PQ}} = 1\)

Vậy ∆ DEF đồng dạng ∆ QMP theo tỉ số đồng dạng k = 1, trong đó D, E, F lần lượt tương ứng với các đỉnh Q, M, P.

b. Lục giác DPEQFM có các cặp cạnh đối bằng nhau từng đôi một:

DP = QF (vì bằng \({1 \over 2}\)OA);

PE = MF (vì bằng  \({1 \over 2}\)OC)

EQ = MD (vì bằng \({1 \over 2}\)OB)

Lục giác DPEQFM có 6 cạnh bằng nhau chỉ khi DP = PE = EQ.

Muốn vậy, ta phải có OA = OB = OC, khi đó O là điểm cách đều ba điểm A, B, C. Vậy O là giao điểm của ba đường trung trực tam giác ABC.

Sachbaitap.com