Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9 trang 51 SGK Toán 9 Chân trời sáng tạo tập 1

Bài 1 trang 51 SGK Toán 9 tập 1 - Chân trời sáng tạo

Tính

a) \(\sqrt {{{\left( { - 10} \right)}^2}} \)

b) \(\sqrt {{{\left( { - \frac{2}{7}} \right)}^2}} \)

c) \({\left( { - \sqrt 2 } \right)^2} - \sqrt {25} \)

d) \({\left( { - \sqrt {\frac{2}{3}} } \right)^2}.\sqrt {0,09} \)

Phương pháp:

Dựa vào \({\left( {\sqrt a } \right)^2} = {\left( { - \sqrt a } \right)^2} = a\) và \(\sqrt {{a^2}}  = a\). ( a > 0)

Lời giải:

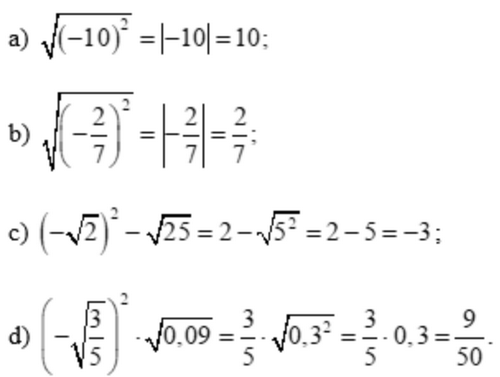
Bài 2 trang 51 SGK Toán 9 tập 1 - Chân trời sáng tạo

Rút gọn các biểu thức sau:

a) \(\sqrt {{{\left( {3 - \sqrt {10} } \right)}^2}} \)

b) \(2\sqrt {{a^2}}  + 4a\) với a < 0

c) \(\sqrt {{a^2}}  + \sqrt {{{\left( {3 - a} \right)}^2}} \) với 0 < a < 3

Phương pháp:

Dựa vào tính chất: Với biểu thức A bất kì, ta có \(\sqrt {{A^2}}  = \left| A \right|\), nghĩa là:

\(\sqrt {{A^2}}  = A\) khi \(A \ge 0\)

\(\sqrt {{A^2}}  =  - A\) khi \(A < 0\)

Lời giải:

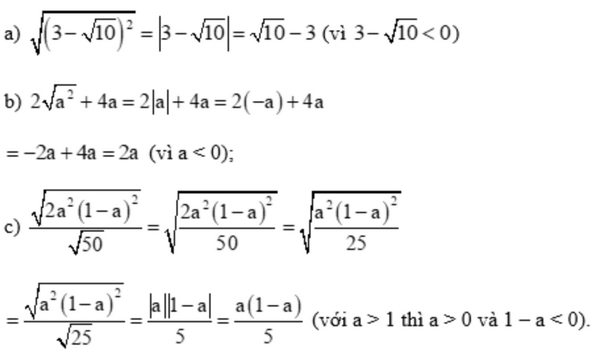
Bài 3 trang 51 SGK Toán 9 tập 1 - Chân trời sáng tạo

Tính

a) \(\sqrt {16.0,25} \)

b) \(\sqrt {{2^4}.{{( - 7)}^2}} \)

c) \(\sqrt {0,9} .\sqrt {1000} \)

d) \(\sqrt 2 .\sqrt 5 .\sqrt {40} \)

Phương pháp:

Dựa vào tính chất \(\sqrt {a.b}  = \sqrt a .\sqrt b \) với a, b > 0

Lời giải:

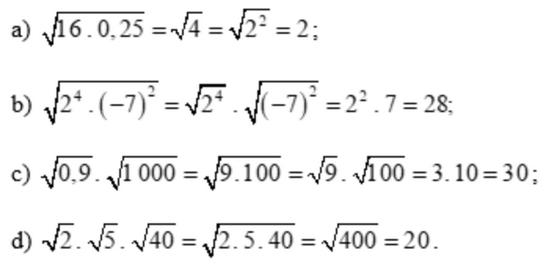
Bài 4 trang 51 SGK Toán 9 tập 1 - Chân trời sáng tạo

Rút gọn các biểu thức sau:

a) \(\sqrt {{8^2}.5} \)

b) \(\sqrt {81{a^2}} \) với a < 0

c) \(\sqrt {5a} .\sqrt {45a}  - 3a\) với a \( \ge \) 0

Phương pháp:

Dựa vào tính chất \(\sqrt {A.B}  = \sqrt A .\sqrt B \) với A, B > 0

Lời giải:

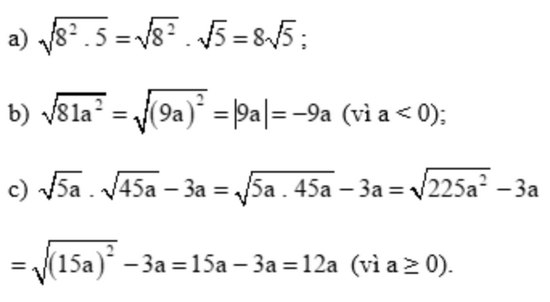
Bài 5 trang 51 SGK Toán 9 tập 1 - Chân trời sáng tạo

Tính

a) \(\sqrt {\frac{{0,49}}{{81}}} \)

b) \(\sqrt {2\frac{7}{9}} \)

c) \(\sqrt {\frac{1}{{16}}.\frac{9}{{36}}} \)

d) \(\left( { - \sqrt {52} } \right):\sqrt {13} \)

Phương pháp:

Dựa vào tính chất: Với số thực a không âm và số thực b dương, ta có:

\(\sqrt {\frac{a}{b}}  = \frac{{\sqrt a }}{{\sqrt b }}\)

Lời giải:

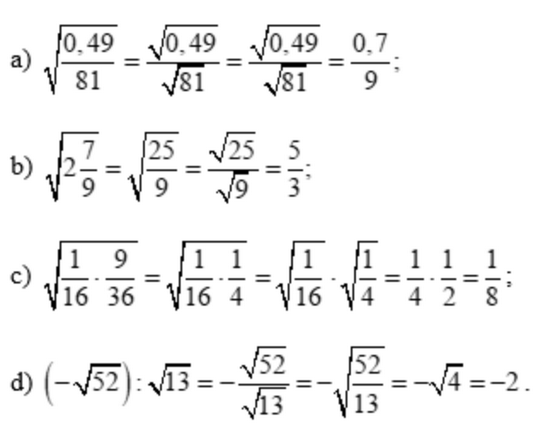
Bài 6 trang 51 SGK Toán 9 tập 1 - Chân trời sáng tạo

Rút gọn các biểu thức sau:

a) \(\frac{{\sqrt 5 .\sqrt 6 }}{{\sqrt {10} }}\)

b) \(\frac{{\sqrt {24{a^3}} }}{{\sqrt {6a} }}\) với a > 0

c) \(\sqrt {\frac{{3{a^2}b}}{{27}}} \) với \(a \le 0;b \ge 0\)

Phương pháp:

Dựa vào tính chất: Với biểu thức A không âm và biểu thức B dương, ta có:

\(\sqrt {\frac{A}{B}}  = \frac{{\sqrt A }}{{\sqrt B }}\)

Lời giải:

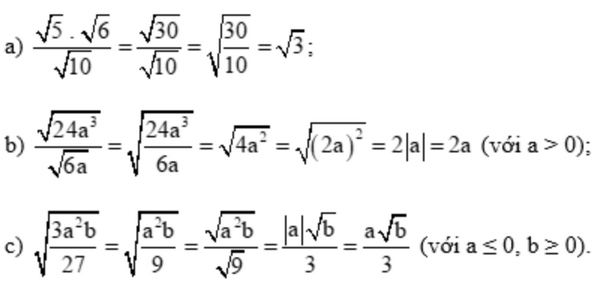
Bài 7 trang 51 SGK Toán 9 tập 1 - Chân trời sáng tạo

Cho hình chữ nhật có chiều rộng a (cm), chiều dài b (cm) và diện tích S (cm²)

a) Tìm S, biết a = \(\sqrt 8 \); b = \(\sqrt {32} \).

b) Tìm b, biết S = \(3\sqrt 2 \); a = \(2\sqrt 3 \)

Phương pháp:

Dựa vào công thức tính diện tích hình chữ nhật S = a.b (a: chiều rộng, b: chiều dài).

Lời giải:

a) Diện tích S của hình chữ nhật là:

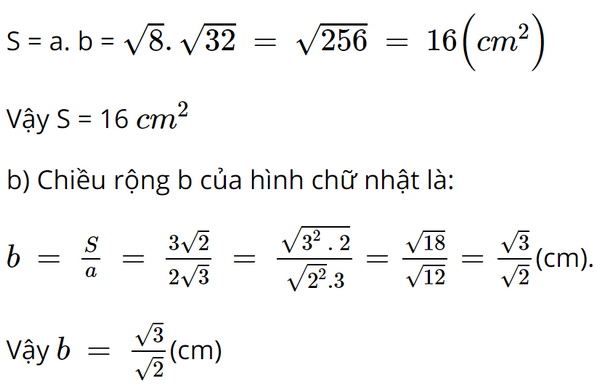
Bài 8 trang 51 SGK Toán 9 tập 1 - Chân trời sáng tạo

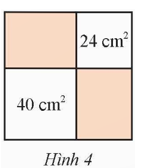
Từ một tấm thép hình vuông, người thợ cắt hai mảnh hình vuông có diện tích lần lượt là 24 cm² và 40 cm² như Hình 4. Tính diện tích phần còn lại của tấm thép.

Phương pháp:

Dựa vào công thức tính diện tích hình vuông S = a² (a: độ dài cạnh).

Lời giải:

Cạnh của hình vuông có diện tích 24 cm² là:

Hai hình chữ nhật còn lại có chiều dài bằng nhau (đều bằng cạnh của hình vuông có diện tích 40 cm²) và có chiều rộng bằng nhau (đều bằng cạnh của hình vuông có diện tích 24 cm²).

Giải câu hỏi đố vui trang 41 SGK Toán 9 tập 1 - Chân trời sáng tạo

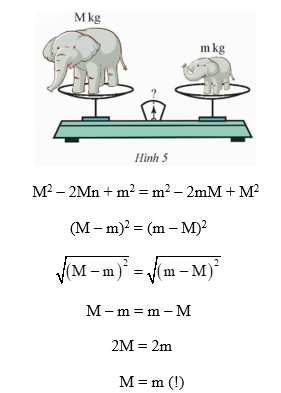
Tìm chỗ sai trong phép chứng minh “voi con nặng bằng voi mẹ” sau đây:

Phương pháp:

Dựa vào tính chất: Với biểu thức A bất kì, ta có \(\sqrt{{{A}^{2}}}=\left| A \right|\), nghĩa là:

\(\sqrt{{{A}^{2}}}=A\) khi \(A\ge 0\)

\(\sqrt{{{A}^{2}}}=-A\) khi \(A<0\)

Lời giải:

Phép chứng minh trên sai khi đưa thừa số ra ngoài dấu căn.

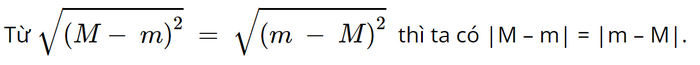
• Nếu M ≥ m thì |M – m| = |m – M| = M – m;

• Nếu M < m thì |M – m| = |m – M| = m – M;

Do đó phép biến đổi từ |M – m| = |m – M| suy ra M – m = m – M là sai.

Sachbaitap.com