Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 63, 64 SGK Toán 6 tập 1 Chân trời sáng tạo
Giải SGK Toán lớp 6 trang 63, 64 tập 1 Chân trời sáng tạo - Bài 3. Phép cộng và phép trừ hai số nguyên. Bài 5 trang 64: Thực hiện các phép tính sau:
Bài 1 trang 63 SGK Toán 6 tập 1 - Chân trời sáng tạo
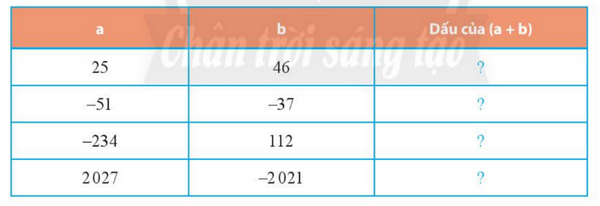
Không thực hiện phép tính, tìm dấu thích hợp thay cho dấu ? ở bảng sau:
Phương pháp:
Xác định dấu của a và b.
Nếu a và b cùng dấu dương thì (a+b) mang dấu dương (+).
Nếu a và b cùng dấu âm thì (a+b) mang dấu âm(-).
Nếu số dương lớn hơn số đối của số âm thì (a+b) mang dấu dương.
Nếu số dương bé hơn số đối của số âm thì (a+b) mang dấu âm.
Lời giải:
+) Với a = 25, b = 46 ta nhận thấy cả a và b đều là số nguyên dương nên dấu của (a + b) là dương.
+) Với a = - 51, b = -37 ta nhận thấy cả a và b đều là số nguyên âm nên dấu của (a + b) là âm.
+) Với a = - 234, b = 112 ta thấy a là số nguyên âm, b là số nguyên dương và 234 > 112 nên dấu của (a + b) là âm.
+) Với a = 2027, b = - 2021 ta thấy a là số nguyên dương, b là số nguyên âm và a > b nên dấu của (a + b) là dương.
Ta hoàn thành bảng sau:
|
a |
b |
Dấu (a + b) |
|
25 |
46 |
+ |
|
- 51 |
- 37 |
- |
|
- 234 |
112 |
- |
|
2027 |
- 2021 |
+ |
Bài 2 trang 63 SGK Toán 6 tập 1 - Chân trời sáng tạo
Thực hiện các phép tính sau:
a) 23+45
b) \(\left( { - 42} \right) + \left( { - 54} \right)\)
c) \(2025 + \left( { - 2025} \right)\);
d) \(15 + \left( { - 14} \right)\);
e) \(35 + \left( { - 135} \right)\)
Phương pháp:
- Xác định dấu của hai số hạng trong phép cộng.
- Muốn cộng hai số nguyên dương, ta cộng chúng như cộng hai số tự nhiên.
- Muốn cộng hai số nguyên âm, ta cộng hai số đối của chúng rồi thêm dấu trừ đằng trước kết quả.
- Nếu số dương lớn hơn số đối của số âm thì ta lấy số dương trừ đi số đối của số âm.
- Nếu số dương bé hơn số đối của số âm thì ta lấy số đối của số âm trừ đi số dương rồi thêm dấu trừ trước kết quả.
Lời giải:
a) 23 + 45 = 68
b) (-42) + (-54) = - (42 + 54) = - 96;
c) 2 025 + (-2 025) = 0;
d) 15 + (-14) = (15 – 14) = 1;
e) 35 + (-135) = - (135 – 35) = - 100.
Bài 3 trang 63 SGK Toán 6 tập 1 - Chân trời sáng tạo
Em hãy dùng số nguyên âm để giải bài toán sau:
Một chiếc tàu ngầm đang ở độ sâu 20 m, tàu tiếp tục lặn xuống thêm 15 m nữa. Hỏi khi đó, tàu ngầm ở độ sâu là bao nhiêu mét?
Phương pháp:
Độ sâu của tàu ngầm được biểu diễn là số nguyên âm.
Lặn xuống được biểu diễn là số nguyên âm.
Lời giải:
Tàu ngầm đang ở độ sâu 20 m hay tàu đang ở độ cao: - 20 m;
Tàu lặn thêm 15 m nữa được biểu diễn bởi: - 15m;
Khi đó tàu ngầm ở : (- 20) + (-15) = - 35 (m)
Do đó tàu ngầm ở độ cao - 35 m hay tàu ở độ sâu 35 m.
Vậy độ sâu của tàu ngầm ở độ sâu 35 m.
Bài 4 trang 64 SGK Toán 6 tập 1 - Chân trời sáng tạo
Một tòa nhà có 12 tầng và 3 tầng hầm (tầng G được đánh số là tầng 0), hãy dùng phép cộng các số nguyên để diễn tả tình huống sau đây: Một thang máy đang ở tầng 3, nó đi lên 7 tầng và sau đó đi xuống 12 tầng. Hỏi cuối cùng thang máy dừng lại tại tầng mấy?

Phương pháp:
Biểu diễn các tầng bằng số nguyên.
Thang máy đi lên ta làm phép tính cộng.
Thang máy đi xuống ta làm phép tính trừ.
Lời giải:
Thang máy đang ở tầng 3 đi lên 7 tầng và sau đó đi xuống 12 tầng sẽ đến: 3 + 7 – 12 = 10 – 12 = -2.
Nghĩa là lúc này thang máy đang ở tầng hầm thứ hai.
Bài 5 trang 64 SGK Toán 6 tập 1 - Chân trời sáng tạo
Thực hiện các phép tính sau:
a) \(6 - 8\)
b) \(3 - \left( { - 9} \right)\)
c) \(\left( { - 5} \right) - 10\)
d) \(0 - 7\)
e) \(4 - 0\)
g) \(\left( { - 2} \right) - \left( { - 10} \right)\)
Phương pháp:
- Xác định số trừ.
- Tìm số đối của số trừ.
- Lấy số bị trừ cộng với số đối của số trừ.
- Sử dụng quy tắc cộng hai số nguyên.
- Một số cộng với 0 bằng chính nó.
Lời giải:
a) 6 – 8 = 6 + (-8) = -2;
b) 3 – (-9) = 3 + 9 = 12;
c) (-5) – 10 = - (10 + 5) = -15;
d) 0 – 7 = -7;
e) 4 – 0 = 4;
g) (-2) – (-10) = (-2) + 10 = 10 – 2 = 8.
Bài 6 trang 64 SGK Toán 6 tập 1 - Chân trời sáng tạo
Tính nhanh các tổng sau:
a) \(S = \left( {45 - 3756} \right) + 3756\)
b) \(S = \left( { - 2021} \right) - \left( {199 - 2021} \right)\)
Phương pháp:
Sử dụng quy tắc dấu ngoặc.
Trước dấu ngoặc có dấu “+” thì bỏ dấu ngoặc và giữ nguyên dấu của các số hạng.
Trước dấu ngoặc có dấu “-” thì bỏ dấu ngoặc và đổi dấu tất cả các số hạng trong ngoặc.
Sau đó sử dụng quy tắc cộng trừ hai số nguyên và tính chất của phép cộng.
Lời giải:
a) S = (45 – 3 756) + 3 756 = 45 – 3 756 + 3 756 = 45 + [(– 3 756) + 3 756] = 45 + 0 = 45
b) S = (-2 021) - (199 – 2 021) = (-2 021) + (-199) + 2 021
= [(-2 021) + 2 021] + (- 199) = 0 + (- 199) = - 199
Bài 7 trang 64 SGK Toán 6 tập 1 - Chân trời sáng tạo
Bỏ dấu ngoặc rồi tính:
a) \(\left( {4 + 32 + 6} \right) + \left( {10 - 36 - 6} \right)\)
b) \(\left( {77 + 22 - 65} \right) - \left( {67 + 12 - 75} \right)\)
c) \( - \left( { - 21 + 43 + 7} \right) - \left( {11 - 53 - 17} \right)\)
Phương pháp:
Nếu đằng trước ngoặc là dấu "+" ta bỏ ngoăcc và giữ nguyên dấu các số hạng trong ngoặc.
Nếu đằng trước ngoặc là dấu "-" ta bỏ ngoặc và đổi dấu các số hạng trong ngoặc.
Lời giải:
a) (4 + 32 + 6) + (10 – 36 - 6)
= 4 + 32 + 6 + 10 – 36 – 6
= 36 + 6 + 10 – 36 – 6
= (36 – 36) + ( 6 – 6) + 10
= 0 + 0 + 10
= 10.
b) (77 + 22 – 65) - (67 + 12 - 75)
= 77 + 22 – 65 – 67 – 12 + 75
= (77 – 67) + (22 – 12) + ( - 65 + 75)
= 10 + 10 + 10
= 30.
c) - (-21 + 43 + 7) – (11 – 53 - 17)
= 21 – 43 – 7 – 11 + 53 + 17
= (21 – 11) + ( -43 + 53) + (-7 + 17)
= 10 + 10 + 10
= 30.
Bài 8 trang 64 SGK Toán 6 tập 1 - Chân trời sáng tạo
Archimedes (Ác-si-mét) là nhà bác học người Hi Lạp, ông sinh năm 287 TCN và mất năm 212 TCN.

a) Em hãy dùng số nguyên âm để ghi năm sinh, năm mất của Archimedes.
b) Em hãy cho biết Archimedes mất năm bao nhiêu tuổi.
Phương pháp:
a) Năm trước công nguyên được biểu diễn bởi số nguyên âm.
b) Sử dụng quy tắc trừ hai số nguyên âm tính tuổi của Archimedes.
Lời giải:
a)
Archimedes sinh năm 287 TCN hay năm sinh của Archimedes là năm - 287
Ông mất năm 212 TCN hay năm mất của Archimedes: - 212
b) Ta tính tuổi của Archimedes bằng cách lấy năm mất trừ đi năm sinh.
Tuổi của nhà bác học là: (-212) – (-287) = (-212) + 287 = 75 (tuổi)
Vậy Archimedes mất năm 75 tuổi.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải bài 1, 2, 3, 4, 5, 6 trang 107 SGK Toán 6 tập 2 Chân trời sáng tạo (19/08)
- Giải bài 1, 2, 3, 4 trang 105 SGK Toán 6 tập 2 Chân trời sáng tạo (19/08)
- Giải bài 1, 2, 3, 4 trang 102 SGK Toán 6 tập 2 Chân trời sáng tạo (19/08)
- Giải bài 1, 2, 3, 4, 5 trang 96, 97, 98 SGK Toán 6 tập 2 Chân trời sáng tạo (19/08)
- Giải bài 1, 2, 3, 4 trang 91 SGK Toán 6 tập 2 Chân trời sáng tạo (19/08)
- Bài tập cuối chương 5
- Bài 8. Hoạt động thực hành và trải nghiệm. Phân số ở quanh ta
- Bài 7. Hỗn số
- Bài 6. Giá trị phân số của một số
- Bài 5. Phép nhân và phép chia phân số
- Bài 4. Phép cộng và phép trừ phân số
- Bài 3. So sánh phân số
- Bài 2. Tính chất cơ bản của phân số
- Bài 1. Phân số với tử số và mẫu số là số nguyên
- Bài tập cuối chương 9
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
