Giải bài 1, 2, 3, 4, 5, 6 trang 34 SGK Toán 9 Chân trời sáng tạo tập 1
Một kì thi Tiếng anh bao gồm bốn kĩ năng: nghe, nói, đọc và viết. Kết quả của bài thi là điểm số trung bình của bốn kĩ năng này. Bạn Hà đã đạt được điểm số của ba kĩ năng nghe, đọc, viết lần lượt là 6,5; 6,5; 5,5. Hỏi bạn Hà cần đạt bao nhiêu điểm trong kĩ năng nói để đạt được của bài thi ít nhất là 6,25?
Bài 1 trang 34 SGK Toán 9 tập 1 - Chân trời sáng tạo
Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
a) 2x – 5 > 0;
b) 3y + 1 \( \ge \) 0;
c) 0x - 3 < 0;
d) x2 > 0.
Phương pháp:
Dựa vào định nghĩa bất phương trình dạng ax + b > 0 (a \( \ne \) 0).
Lời giải:
a) 2x – 5 > 0 là bất phương trình một ẩn vì có dạng ax + b > 0 với a = 2 ≠ 0 và b = –5;
b) 3y + 1 ≥ 0 là bất phương trình một ẩn vì có dạng ax + b ≥ 0 với a = 3 ≠ 0 và b = 1;
c) 0x – 3 < 0 không phải phương trình bậc nhất một ẩn vì a = 0;
d) x2 > 0 không phải phương trình bậc nhất một ẩn vì x2 có bậc là 2.
Bài 2 trang 34 SGK Toán 9 tập 1 - Chân trời sáng tạo
Tìm x sao cho:
a) Giá trị của biểu thức 2x + 1 là số dương
b) Giá trị biểu thức 3x – 5 là số âm.
Phương pháp:
Dựa vào giá trị biểu thức là số dương thì biểu thức lớn hơn 0, giá trị biểu thức là số âm thì biểu thức nhỏ hơn 0.
Lời giải:
a) Giá trị của biểu thức 2x + 1 là số dương. Ta có:
2x + 1 > 0
2x > –1

b) Giá trị của biểu thức 3x – 5 là số âm. Ta có:
3x – 5 < 0
3x < 5

Bài 3 trang 34 SGK Toán 9 tập 1 - Chân trời sáng tạo
Giải các bất phương trình
a) 6 < x – 3
b) \(\frac{1}{2}\)x > 5
c) – 8x + 1 \( \ge \) 5
d) 7 < 2x + 1
Phương pháp:
Dựa vào cách giải bất phương trình bậc nhất một ẩn:
Xét bất phương trình ax + b > 0 (a \( \ne \) 0)
- Cộng hai vế của bất phương trình với – b, ta được bất phương trình:
ax > - b
- Nhân hai vế của bất phương trình nhận được với \(\frac{1}{a}\):
+ Nếu a > 0 thì nhận được nghiệm của bất phương trình đã cho là \(x > - \frac{b}{a}\)
+ Nếu a < 0 thì nhận được nghiệm của bất phương trình đã cho là \(x < - \frac{b}{a}\)
Lời giải:
a) Ta có: 6 < x – 3
9 < x.
Vậy nghiệm của bất phương trình là 9 < x.
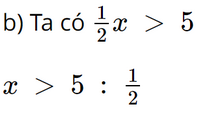
x > 10.
Vậy nghiệm của bất phương trình là x > 10.
c) Ta có –8x + 1 ≥ 5
–8x ≥ 4

d) Ta có 7 < 2x + 1
6 < 2x
3 < x.
Vậy nghiệm của bất phương trình là 3 < x.
Bài 4 trang 34 SGK Toán 9 tập 1 - Chân trời sáng tạo
Giải các bất phương trình
a) x – 7 < 2 – x
b) x + 2 \( \le \) 2 + 3x
c) 4 + x > 5 – 3x
d) –x + 7 \( \ge \) x – 3
Phương pháp:
Dựa vào cách giải bất phương trình bậc nhất một ẩn:
Xét bất phương trình ax + b > 0 (a \( \ne \) 0)
- Cộng hai vế của bất phương trình với – b, ta được bất phương trình:
ax > - b
- Nhân hai vế của bất phương trình nhận được với \(\frac{1}{a}\):
+ Nếu a > 0 thì nhận được nghiệm của bất phương trình đã cho là \(x > - \frac{b}{a}\)
+ Nếu a < 0 thì nhận được nghiệm của bất phương trình đã cho là \(x < - \frac{b}{a}\)
Lời giải:
a) Ta có: x – 7 < 2 – x
2x < 9

b) Ta có: x + 2 ≤ 2 + 3x
2 – 2 ≤ 3x – x
0 ≤ 2x
x ≥ 0.
Vậy nghiệm của bất phương trình là x ≥ 0.
c) Ta có: 4 + x > 5 – 3x
4x > 1

d) Ta có: –x + 7 ≥ x – 3
–2x ≥ –10
–x ≥ –5
x ≤ 5.
Vậy nghiệm của bất phương trình là x ≤ 5.
Bài 5 trang 34 SGK Toán 9 tập 1 - Chân trời sáng tạo
Giải các bất phương trình
a) \(\frac{2}{3}(2x + 3) < 7 - 4x\)
b) \(\frac{1}{4}(x - 3) \le 3 - 2x\)
Phương pháp:
Dựa vào cách giải bất phương trình bậc nhất một ẩn:
Xét bất phương trình ax + b > 0 (a \( \ne \) 0)
- Cộng hai vế của bất phương trình với – b, ta được bất phương trình:
ax > - b
- Nhân hai vế của bất phương trình nhận được với \(\frac{1}{a}\):
+ Nếu a > 0 thì nhận được nghiệm của bất phương trình đã cho là \(x > - \frac{b}{a}\)
+ Nếu a < 0 thì nhận được nghiệm của bất phương trình đã cho là \(x < - \frac{b}{a}\)
Lời giải:

Bài 6 trang 34 SGK Toán 9 tập 1 - Chân trời sáng tạo
Một kì thi Tiếng anh bao gồm bốn kĩ năng: nghe, nói, đọc và viết. Kết quả của bài thi là điểm số trung bình của bốn kĩ năng này. Bạn Hà đã đạt được điểm số của ba kĩ năng nghe, đọc, viết lần lượt là 6,5; 6,5; 5,5. Hỏi bạn Hà cần đạt bao nhiêu điểm trong kĩ năng nói để đạt được của bài thi ít nhất là 6,25?
Phương pháp:
Đọc kĩ dữ liệu đề bài để lập ra bất phương trình bậc nhất 1 ẩn.
Lời giải:
Gọi x là điểm của kĩ năng nói.
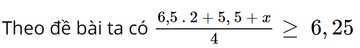
18,5 + x ≥ 25
x ≥ 25 – 18,5
x ≥ 6,5.
Vậy bạn Hà cần đạt ít nhất 6,5 điểm nói.
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải câu hỏi trang 112 SGK Toán 9 Chân trời sáng tạo tập 1 (22/07)
- Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 trang 103 SGK Toán 9 Chân trời sáng tạo tập 1 (22/07)
- Giải bài 1, 2, 3, 4, 5, 6, 7 trang 102 SGK Toán 9 Chân trời sáng tạo tập 1 (22/07)
- Giải bài 1, 2, 3, 4, 5, 6, 7 trang 97 SGK Toán 9 Chân trời sáng tạo tập 1 (22/07)
- Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 88 SGK Toán 9 Chân trời sáng tạo tập 1 (22/07)
- Hoạt động thực hành và trải nghiệm
- Bài tập cuối chương 5
- Bài 4: Hình quạt tròn và hình vành khuyên
- Bài 3: Góc ở tâm, góc nội tiếp
- Bài 2: Tiếp tuyến của đường tròn
- Bài 1: Đường tròn
- Chương 5: Đường tròn
- Bài tập cuối chương 4
- Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông
- Bài 1: Tỉ số lượng giác của góc nhọn
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
