Giải bài 1, 2, 3, 4, 5 trang 14 SGK Toán 9 Chân trời sáng tạo tập 1
Cho hai đường thẳng (y = - frac{1}{2}x + 2) và y = -2x – 1.a) Vẽ hai đường thẳng đó trên cùng mặt phẳng toạ độ Oxy.b) Xác định toạ độ giao điểm A của hai đường thẳng trên. c) Tọa độ của điểm A có là nghiệm của hệ phương trình
Bài 1 trang 14 SGK Toán 9 tập 1 - Chân trời sáng tạo
Trong các phương trình sau, phương trình nào là phương trình bậc nhất hai ẩn? Xác định các hệ số a, b, c của mỗi phương trình bậc nhất hai ẩn đó.
a) 2x + 5y = -7;
b) 0x – 0y = 5;
c) 0x - \(\frac{5}{4}y\)= 3;
d) 0,2x + 0y = -1,5.
Phương pháp:
Dựa vào khái niệm phương trình bậc nhất hai ẩn x và y là hệ thức có dạng
\(ax + by = c\)
Trong đó, a và b không đồng thời bằng 0.
Lời giải:
a) 2x + 5y = –7 là phương trình bậc nhất hai ẩn với a = 2, b = 5, c = –7.
b) 0x – 0y = 5 không phải là phương trình bậc nhất hai ẩn vì a = 0 và b = 0.

d) 0,2x + 0y = –1,5 là phương trình bậc nhất hai ẩn với a = 0,2; b = 0; c = –1,5.
Bài 2 trang 14 SGK Toán 9 tập 1 - Chân trời sáng tạo
Trong các cặp số (1;1), (-2;5), (0;2), cặp số nào là nghiệm của mỗi phương trình sau?
a) 4x + 3y = 7;
b) 3x – 4y = -1.
Phương pháp:
Thay lần lượt từng cặp nghiệm vào mỗi phương trình để kiểm tra.
Lời giải:
a) Cặp số (1; 1) là nghiệm của phương trình 4x + 3y = 7 vì 4 . 1 + 3 . 1 = 4 + 3 = 7.
Cặp số (–2; 5) là nghiệm của phương trình 4x + 3y = 7 vì 4 . (–2) + 3 . 5 = –8 + 15 = 7.
Cặp số (0; 2) không phải là nghiệm của phương trình 4x + 3y = 7 vì 4 . 0 + 3 . 2 = 6 ≠ 7.
Vậy trong các cặp số đã cho thì có hai cặp số (1; 1) và (–2; 5) là nghiệm của phương trình 4x + 3y = 7.
a) Cặp số (1; 1) là nghiệm của phương trình 3x – 4y = –1 vì 3 . 1 – 4 . 1 = 3 – 4 = –1.
Cặp số (–2; 5) không phải là nghiệm của phương trình 3x – 4y = –1 vì 3 . (–2) – 4 . 5 = 6 – 20 = –26 ≠ –1.
Cặp số (0; 2) không phải là nghiệm của phương trình 3x – 4y = –1 vì 3 . 0 – 4 . 2 = 0 – 8 = –8 ≠ –1.
Vậy trong các cặp số đã cho thì có cặp số (1; 1) là nghiệm của phương trình 3x – 4y = –1.
Bài 3 trang 14 SGK Toán 9 tập 1 - Chân trời sáng tạo
Hãy biểu diễn tất cả các nghiệm của mỗi phương trình sau trên mặt phẳng toạ độ Oxy.
a) 2x + y = 3;
b) 0x – y = 3;
c) – 3x + 0y = 2;
d) -2x + y = 0.
Phương pháp:
Dựa vào VD3 trang 11 để vẽ các nghiệm trên mặt phẳng toạ độ Oxy.
Lời giải:
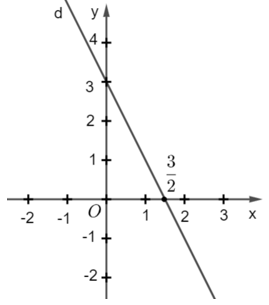
a) Viết lại phương trình thành y = –2x + 3.
Từ đó, tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng d: y = –2x + 3 (như hình vẽ).
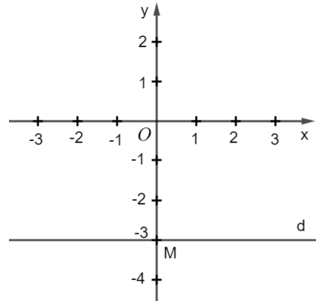
b) Viết lại phương trình thành y = –3.
Từ đó, tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng d vuông góc với Oy tại điểm M(0; –3).
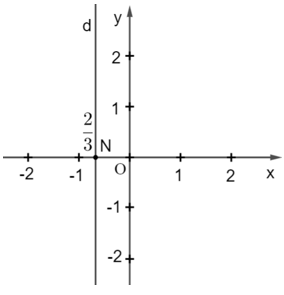
c) Viết lại phương trình thành x= 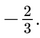
Từ đó, tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng d vuông góc với Ox tại điểmN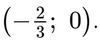
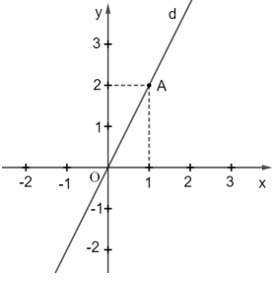
d) Viết lại phương trình thành y = 2x.
Từ đó, tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng d: y = 2x
Đường thẳng d đi qua gốc tọa độ O và điểm A(1; 0) (như hình vẽ).
Bài 4 trang 14 SGK Toán 9 tập 1 - Chân trời sáng tạo
Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{4x - y = 2}\\{x + 3y = 7.}\end{array}} \right.\)
Cặp số nào dưới đây là nghiệm của hệ phương trình đã cho?
a) (2;2)
b) (1;2)
c) (-1;-2).
Phương pháp:
Thay lần lượt từng cặp nghiệm vào hệ phương trình để kiểm tra.
Lời giải:

Bài 5 trang 14 SGK Toán 9 tập 1 - Chân trời sáng tạo
Cho hai đường thẳng \(y = - \frac{1}{2}x + 2\) và y = -2x – 1.
a) Vẽ hai đường thẳng đó trên cùng mặt phẳng toạ độ Oxy.
b) Xác định toạ độ giao điểm A của hai đường thẳng trên.
c) Toạ độ của điểm A có là nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + 2y = 4}\\{2x + y = - 1}\end{array}} \right.\) không? Tại sao?
Phương pháp:
- Dựa vào VD3 trang 11 để vẽ các nghiệm trên mặt phẳng toạ độ Oxy.
- Nhìn vào đồ thị hàm số cắt nhau tại đâu chính là điểm A.
- Thay toạ độ điểm A vào hệ phương trình để kiểm tra.
Lời giải:
a) Đường thẳng 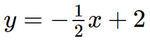 đi qua điểm M(0; 2) và điểm N(2; 1).
đi qua điểm M(0; 2) và điểm N(2; 1).
Đường thẳng y = –2x – 1 đi qua điểm P(0; –1) và điểm Q(–1; 1).
Ta vẽ hai đường thẳng đó trên cùng mặt phẳng tọa độ Oxy như sau:
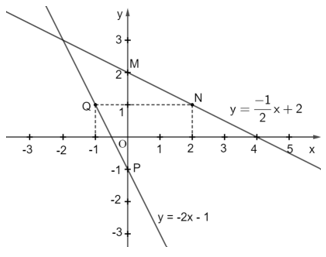
b) Giao điểm A của hai đường thẳng 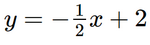 và y = –2x – 1 được biểu diễn như sau:
và y = –2x – 1 được biểu diễn như sau:
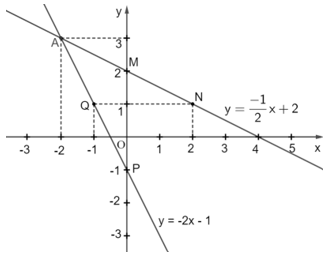
Dóng điểm A lên hai trục Ox và Oy, ta có A(–2; 3).
Vậy tọa độ giao điểm A của hai đường thẳng 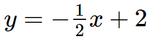 và y = –2x – 1 là A(–2; 3).
và y = –2x – 1 là A(–2; 3).
c) Cặp số (–2; 3) là nghiệm của hệ phương trình đã cho vì
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Giải câu hỏi trang 112 SGK Toán 9 Chân trời sáng tạo tập 1 (22/07)
- Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 trang 103 SGK Toán 9 Chân trời sáng tạo tập 1 (22/07)
- Giải bài 1, 2, 3, 4, 5, 6, 7 trang 102 SGK Toán 9 Chân trời sáng tạo tập 1 (22/07)
- Giải bài 1, 2, 3, 4, 5, 6, 7 trang 97 SGK Toán 9 Chân trời sáng tạo tập 1 (22/07)
- Giải bài 1, 2, 3, 4, 5, 6, 7, 8 trang 88 SGK Toán 9 Chân trời sáng tạo tập 1 (22/07)
- Hoạt động thực hành và trải nghiệm
- Bài tập cuối chương 5
- Bài 4: Hình quạt tròn và hình vành khuyên
- Bài 3: Góc ở tâm, góc nội tiếp
- Bài 2: Tiếp tuyến của đường tròn
- Bài 1: Đường tròn
- Chương 5: Đường tròn
- Bài tập cuối chương 4
- Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông
- Bài 1: Tỉ số lượng giác của góc nhọn
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
