Giải bài 1, 2, 3, 4, 5 trang 18 SGK Toán 6 tập 2 Chân trời sáng tạo

Bài 1 trang 18 SGK Toán 6 tập 2 - Chân trời sáng tạo

Tính giá trị các biểu thức sau theo hai cách (có cách dùng tính chất phép cộng):

a) \(\left( {\frac{{ - 2}}{{ - 5}} + \frac{{ - 5}}{{ - 6}}} \right) + \frac{4}{5}\)

b) \(\frac{{ - 3}}{{ - 4}} + \left( {\frac{{11}}{{ - 15}} + \frac{{ - 1}}{2}} \right)\).

Lời giải:

 a) Cách 1:

 \(\begin{array}{l}\left( {\frac{{ - 2}}{{ - 5}} + \frac{{ - 5}}{{ - 6}}} \right) + \frac{4}{5} = \frac{2}{5} + \frac{5}{6} + \frac{4}{5}\\ = \frac{{12}}{{30}} + \frac{{25}}{{30}} + \frac{{24}}{{30}} = \frac{{61}}{{30}}\end{array}\)

Cách 2:

\(\begin{array}{l}\left( {\frac{{ - 2}}{{ - 5}} + \frac{{ - 5}}{{ - 6}}} \right) + \frac{4}{5} = \left( {\frac{2}{5} + \frac{4}{5}} \right) + \frac{5}{6}\\ = \frac{6}{5} + \frac{5}{6} = \frac{{36}}{{30}} + \frac{{25}}{{30}} = \frac{{61}}{{30}}\end{array}\)

b) Cách 1:

 \(\begin{array}{l}\frac{{ - 3}}{{ - 4}} + \left( {\frac{{11}}{{ - 15}} + \frac{{ - 1}}{2}} \right) = \frac{3}{4} + \frac{{ - 11}}{{15}} + \frac{{ - 1}}{2}\\ = \frac{{45}}{{60}} + \frac{{ - 44}}{{60}} + \frac{{ - 30}}{{60}}\\ = \frac{{ - 29}}{{60}}\end{array}\).

Cách 2:

\(\begin{array}{l}\frac{{ - 3}}{{ - 4}} + \left( {\frac{{11}}{{ - 15}} + \frac{{ - 1}}{2}} \right) = \frac{3}{4} + \frac{{ - 11}}{{15}} + \frac{{ - 1}}{2}\\ = \left( {\frac{3}{4} + \frac{{ - 1}}{2}} \right) + \frac{{ - 11}}{{15}}\\ = \left( {\frac{3}{4} + \frac{{ - 2}}{4}} \right) + \frac{{ - 11}}{{15}}\\ = \frac{1}{4} + \frac{{ - 11}}{{15}}\\ = \frac{{15}}{{60}} + \frac{{ - 44}}{{60}}\\ = \frac{{ - 29}}{{60}}\end{array}\)

Bài 2 trang 18 SGK Toán 6 tập 2 - Chân trời sáng tạo

Tìm các cặp phân số đối nhau trong các phân số sau:

\(\frac{{ - 5}}{6}\); \(\frac{{ - 40}}{{ - 10}}\); \(\frac{5}{6}\); \(\frac{{40}}{{ - 10}}\); \(\frac{{10}}{{ - 12}}\).

Phương pháp:

Hai phân số đối nhau nếu tổng của chúng bằng 0.

Lời giải:

Bài 3 trang 18 SGK Toán 6 tập 2 - Chân trời sáng tạo

Người ta mở hai vòi nước cùng chảy vào một bể. Vòi thứ nhất mỗi giờ chảy được \(\frac{1}{7}\) bể, vòi thứ hai mỗi giờ chảy được \(\frac{1}{5}\) bể. Nếu mở đồng thời cả hai vòi, mỗi giờ được mấy phần bể?

Phương pháp:

Lượng nước hai vòi chảy được sau mỗi giờ bằng tổng lượng nước mỗi vòi chảy được mỗi giờ.

Lời giải:

Lượng nước hai vòi chảy được sau mỗi giờ bằng tổng lượng nước mỗi vòi chảy được mỗi giờ.

Nếu mở đồng thời cả hai vòi, mỗi giờ được:

Bài 4 trang 18 SGK Toán 6 tập 2 - Chân trời sáng tạo

Bảo đọc hết một quyển sách trong 4 ngày. Ngày thứ nhất đọc được \(\frac{2}{5}\) quyển sách, ngày thứ hai đọc được \(\frac{1}{3}\) quyển sách, ngày thứ ba đọc được \(\frac{1}{4}\) quyển sách. Hỏi hai ngày đầu Bảo đọc nhiều hơn hay ít hơn hai ngày sau? Tim phân số để chỉ số chênh lệch đó.

Phương pháp:

- Tính số phần quyển sách hai ngày đầu và hai ngày sau Bảo đọc được

- So sánh và tìm hiệu của hai phân số tìm được.

Lời giải:

Hai ngày đầu Bảo đọc được:

\(\frac{2}{5} + \frac{1}{3} = \frac{{11}}{{15}}\) (quyển sách)

Hai ngày sau bảo đọc được là:

\(1 - \frac{{11}}{{15}} = \frac{4}{{15}}\) (quyển sách)

Vì \(\frac{{11}}{{15}} > \frac{4}{{15}}\) nên hai ngày đầu Bảo đọc được nhiều hơn hai ngày sau.

Phân số chỉ số chênh lệch là: \(\frac{{11}}{{15}} - \frac{4}{{15}} = \frac{7}{{15}}\) (quyển sách)

Bài 5 trang 18 SGK Toán 6 tập 2 - Chân trời sáng tạo

Đố vui Viết phân số sau ở dạng tổng các phân số có mẫu số là số tự nhiên khác nhau nhưng có cùng tử số là 1.

a) \(\frac{2}{3}\);           b)\(\frac{8}{{15}}\)

c) \(\frac{7}{8}\);            d) \(\frac{{17}}{{18}}\).

Gợi ý:

a) \(\frac{2}{3} = \frac{1}{2} + ?;\)           

c) \(\frac{7}{8} = \frac{1}{2} + ? + ?;\)

Phương pháp:

Tách các phân số theo mẫu.

Lời giải:

Để tách một phân số thành tổng của các phân số có tử số bằng 1 thì ta cần tách thỏa mãn:

- Các số sau khi tách ra thuộc ước của mẫu số.

- Tổng của hai hay nhiều số đó bằng tử số của phân số đã cho. 

a) Phân số 

Các ước của mẫu là các số tự nhiên: Ư(3) = .

Nhận thấy: tổng của hai số thuộc ước tự nhiên của 3 không có tổng bằng 2.

- Các ước của mẫu là các số tự nhiên: Ư(6) = .

- Các số khác nhau thuộc thuộc tập hợp Ư(6) là số tự nhiên và có tổng bằng 4 là 3 và 1.

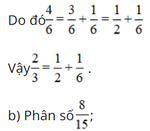
- Các ước của mẫu là các số tự nhiên: Ư(15) = .

- Các số khác nhau thuộc thuộc tập hợp Ư(15) là số tự nhiên và có tổng bằng 8 là 5 và 3.

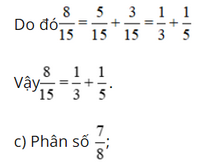
- Các ước của mẫu là các số tự nhiên: Ư(8) = .

- Các số khác nhau thuộc thuộc tập hợp Ư(8) là số tự nhiên và có tổng bằng 7 là 4; 2 và 1.

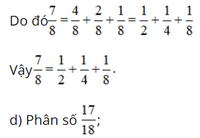
- Các ước của mẫu là các số tự nhiên: Ư(18) = .

- Các số khác nhau thuộc thuộc tập hợp Ư(18) là số tự nhiên và có tổng bằng 17 là 9; 6 và 2.

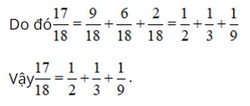
Sachbaitap.com