Giải bài 1, 2, 3, 4 trang 78 SGK Toán 6 tập 2 Chân trời sáng tạo

Bài 1 trang 78 SGK Toán 6 tập 2 - Chân trời sáng tạo

Em hãy chọn trong các phương án dưới đây để được một phát biểu đúng.

Qua hai điểm A và B phân biệt có

(A) vô số đường thẳng,

(B) chỉ có 1 đường thẳng,

(C) không có đường thẳng nào.

Phương pháp:

Qua hai điểm phân biệt chỉ vẽ được 1 đường thẳng.

Lời giải:

Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.

Do đó, qua hai điểm A và B phân biệt chỉ có 1 đường thẳng đi qua hai điểm đó.

Vậy phương án đúng là (B) chỉ có 1 đường thẳng.

Bài 2 trang 78 SGK Toán 6 tập 2 - Chân trời sáng tạo

Vẽ hình cho các trường hợp sau:

a) Hai đường thẳng p và q cắt nhau tại điểm M.

b) Đường thẳng a cắt hai đường thẳng m và n theo thứ tự tại X và Y trong hai trường hợp: m và n cắt nhau, hoặc m và n song song với nhau.

Phương pháp:

- Nếu hai đường thẳng chỉ có một điểm chung, ta nói rằng hai đường thẳng đỏ cắt nhau. Điểm chung được gọi là giao điểm của hai đường thẳng.

- Nếu hai đường thẳng không có điểm chung nào, ta nói rằng hai đường thẳng đó song song với nhau.

Lời giải:

a) Cách vẽ hai đường thẳng p và q cắt nhau tại điểm M: 

Cách 1:

- Vẽ đường thẳng p bất kỳ.

- Vẽ đường thẳng q cắt đường thẳng p.

- Lấy điểm M là giao điểm của hai đường thẳng p và q.

Ta có hình vẽ:

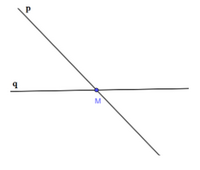
Cách 2: 

- Vẽ đường thẳng p bất kỳ.

- Lấy điểm M thuộc đường thẳng p.

- Vẽ đường thẳng q đi qua điểm M và không trùng với đường thẳng p.

Ta có hình vẽ:

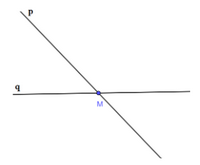
b) Vì đường thẳng a cắt hai đường thẳng m và n theo thứ tự tại X và Y nên ta sẽ không xét trường hợp ba đường thẳng giao nhau tại một điểm. 

Ta xét hai trường hợp còn lại:

- Trường hợp 1: Đường thẳng m và đường thẳng n cắt nhau. Đường thẳng a cắt hai đường thẳng m và n lần lượt tại điểm X và Y.

* Cách vẽ:

- Vẽ đường thẳng m bất kỳ.

- Vẽ đường thẳng n cắt đường thẳng m.

- Vẽ đường thẳng a cắt hai đường thẳng m và n lần lượt tại hai điểm X và Y.

* Ta có hình vẽ:

- Trường hợp 2: Đường thẳng m và đường thẳng n song song với nhau. Đường thẳng a cắt hai đường thẳng m và n lần lượt tại điểm X và Y.

* Cách vẽ:

- Vẽ đường thẳng m bất kỳ.

- Vẽ đường thẳng n song song với đường thẳng m.

- Vẽ đường thẳng a cắt hai đường thẳng m và n lần lượt tại hai điểm X và Y.

* Ta có hình vẽ:

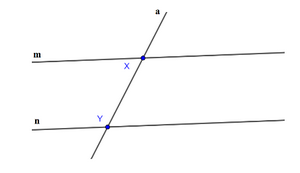
Bài 3 trang 78 SGK Toán 6 tập 2 - Chân trời sáng tạo

Đếm số giao điểm tạo bởi ba đường thẳng trong mỗi hình sau:

Phương pháp:

- Nếu hai đường thẳng chỉ có một điểm chung, ta nói rằng hai đường thẳng đỏ cắt nhau. Điểm chung được gọi là giao điểm của hai đường thẳng.

Lời giải:

a) Trong hình a) có ba đường thẳng song song với nhau nên không có giao điểm nào.

b) Đặt các đường thẳng trong hình b) là các đường thẳng a, b, c. 

Giả sử đường thẳng a và c cắt nhau tại điểm A, đường thẳng b và c cắt nhau tại điểm B (như hình vẽ).

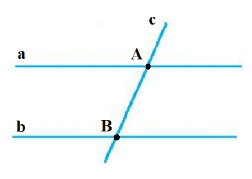
Do đó đường thẳng  a và b cắt đường thẳng c lần lượt tại hai điểm A và B.

Vậy trong hình b) có hai giao điểm tạo bởi ba đường thẳng.

c) Đặt các đường thẳng trong hình c) là các đường thẳng m, n, p.

Giả sử ba đường thẳng m, n, p cắt nhau tại điểm M (như hình vẽ).

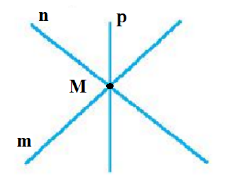
Vậy trong hình c) có một giao điểm tạo bởi ba đường thẳng.

d) Đặt các đường thẳng trong hình d) là các đường thẳng c, d, e.

Giả sử đường thẳng c và e cắt nhau tại điểm C, đường thẳng d và e cắt nhau tại điểm D, đường thẳng c và d cắt nhau tại E (như hình vẽ).

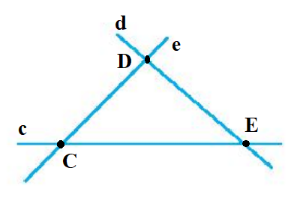
Do đó ba đường thẳng c, d, e đôi một cắt nhau tại các điểm C, D, E.

Vậy trong hình d) có ba giao điểm tạo bởi ba đường thẳng.

Bài 4 trang 78 SGK Toán 6 tập 2 - Chân trời sáng tạo

Kể tên các tia có gốc là M trong hình sau:

Phương pháp:

Mỗi điểm O trên một đường thẳng chia đường thẳng đó thành hai phần, mỗi phần gọi là một tia gốc O.

Lời giải:

Trên hình vẽ, điểm M nằm trên đường thẳng HF chia đường thẳng đó thành hai phần, mỗi phần gọi là một tia gốc M.

Vậy các tia có gốc là M là: tia MH và tia MF.

Sachbaitap.com