Giải SBT Toán 10 trang 61, 62 Cánh Diều tập 2
Giải bài 1, 2, 3, 4, 5, 6, 7 trang 61, bài 8, 9, 10, 11 trang 62 SBT Toán 10 Cánh Diều tập 2. Tìm các số thực a và b sao cho mỗi cặp vectơ sau bằng nhau. Trong mặt phẳng toạ độ Oxy, cho ba điểm không thẳng hàng A(– 4 ; 2), B(2 ; 4), C(8 ; – 2). Tìm toạ độ của điểm D sao cho tứ giác ABCD là hình bình hành.
Bài 1 trang 61 SBT Toán 10 - Cánh Diều
Toạ độ của vectơ \(\overrightarrow u = - 3\overrightarrow i + 2\overrightarrow j \) là:
A. \(( - 3;2)\) B. \((2; - 3)\)
C. \(( - 3\overrightarrow i ;2\overrightarrow j )\) D. \((3;2)\)
Phương pháp:
Áp dụng định lí: Nếu \(\overrightarrow u = a\overrightarrow i + b\overrightarrow j \) thì \(\overrightarrow u = (a;b)\)
Lời giải:
Vậy chọn đáp án A.
Bài 2 trang 61 SBT Toán 10 - Cánh Diều
Tọa độ của vectơ \(\overrightarrow u = 5\overrightarrow j \) là:
A. \((5;0)\) B. \((5;\overrightarrow j )\) C. \((0;5\overrightarrow j )\) D. \((0;5)\)
Phương pháp:
Áp dụng định lí: Nếu \(\overrightarrow u = a\overrightarrow i + b\overrightarrow j \) thì \(\overrightarrow u = (a;b)\)
Lời giải:
Vậy chọn đáp án D.
Bài 3 trang 61 SBT Toán 10 - Cánh Diều
Trong mặt phẳng toạ độ Oxy, cho A(2; −5). Toạ độ của vectơ \(\overrightarrow {OA} \) là:
A. (2 ; 5) B. (2; −5) C. (−2; −5) D. (−2; 5)
Phương pháp:
Áp dụng định nghĩa tọa độ điểm M được gọi là tọa độ của vectơ \(\overrightarrow {OM} \)
Lời giải:
Bài 4 trang 61 SBT Toán 10 - Cánh Diều
Trong mặt phẳng toạ độ Oxy, cho A(−1; 3), B(2; −1). Toạ độ của vectơ \(\overrightarrow {AB} \) là:
A. (1; -4) B. (-3; 4) C. (3; -4) D. (1; -2)
Phương pháp:
Nếu \(A({x_A};{y_A}),B({x_B};{y_B})\) thì \(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A})\)
Lời giải:
Vậy chọn đáp án C.
Bài 5 trang 61 SBT Toán 10 - Cánh Diều
Trong mặt phẳng toạ độ Oxy, cho \(\overrightarrow u = ( - 2; - 4),\overrightarrow v = (2x - y;y)\). Hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) bằng nhau nếu:
A.\(\left\{ \begin{array}{l}x = 1\\y = - 4\end{array} \right.\) B. \(\left\{ \begin{array}{l}x = - 3\\y = - 4\end{array} \right.\) C. \(\left\{ \begin{array}{l}x = 1\\y = 4\end{array} \right.\) D. \(\left\{ \begin{array}{l}x = - 3\\y = 4\end{array} \right.\)
Lời giải:
Ta có: \(\overrightarrow u = \overrightarrow v \Leftrightarrow \left\{ \begin{array}{l}2x - y = - 2\\y = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 3\\y = - 4\end{array} \right.\)
Chọn B
Bài 6 trang 61 SBT Toán 10 - Cánh Diều
Cho hình bình hành ABCD có A(–1 ; –2), B(3; 2), C(4; − 1). Toạ độ của đỉnh D là:
A. (8; 3) B. (3; 8) C. (-5; 0) D. (0; -5)
Lời giải:
Giả sử D(a; b) ta có \(\overrightarrow {DC} = (4 - a; - 1 - b)\) và \(\overrightarrow {AB} = (4;4)\)
ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {DC} = \overrightarrow {AB} \Leftrightarrow \left\{ \begin{array}{l}4 - a = 4\\ - 1 - b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = - 5\end{array} \right. \Rightarrow D(0; - 5)\)
Chọn D
Bài 7 trang 61 SBT Toán 10 - Cánh Diều
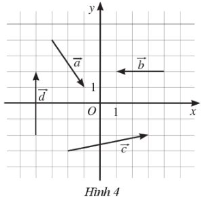
Tìm toạ độ của các vectơ trong Hình 4.
Phương pháp:
Bước 1: Xác định tọa độ các điểm A, B, C, D sao cho \(\overrightarrow {OA} = \overrightarrow a ;\overrightarrow {OB} = \overrightarrow b ;\overrightarrow {OC} = \overrightarrow c ;\overrightarrow {OD} = \overrightarrow d \)
Bước 2: Tìm tọa độ các vectơ \(\overrightarrow a ;\overrightarrow b ;\overrightarrow c ;\overrightarrow d \) dựa vào tọa độ các vectơ \(\overrightarrow {OA} ;\overrightarrow {OB} ;\overrightarrow {OC} ;\overrightarrow {OD} \)
Lời giải:
- Vẽ \(\overrightarrow {OA} = \overrightarrow a \), ta có \(A(2; - 3)\) nên \(\overrightarrow a = (2; - 3)\)
- Vẽ \(\overrightarrow {OB} = \overrightarrow b \), ta có \(B( - 3;0)\) nên \(\overrightarrow b = ( - 3;0)\)
- Vẽ \(\overrightarrow {OC} = \overrightarrow c \), ta có \(C(5;1)\) nên \(\overrightarrow c = (5;1)\)
- Vẽ \(\overrightarrow {OD} = \overrightarrow d \), ta có \(D(0;4)\) nên \(\overrightarrow d = (0;4)\)
Bài 8 trang 62 SBT Toán 10 - Cánh Diều
Tìm các số thực a và b sao cho mỗi cặp vectơ sau bằng nhau:
a) \(\overrightarrow m = (2a + 3;b - 1)\) và \(\overrightarrow n = (1; - 2)\)
b) \(\overrightarrow u = (3a - 2;5)\)và \(\overrightarrow v = (5;2b + 1)\)
c) \(\overrightarrow x = (2a + b;2b)\) và \(\overrightarrow y = (3 + 2b;b - 3a)\)
Phương phảp:
\(\overrightarrow a = ({x_1};{y_1})\) và \(\overrightarrow b = ({x_2};{y_2})\) bằng nhau khi và chỉ khi \(\left\{ \begin{array}{l}{x_1} = {x_2}\\{y_1} = {y_2}\end{array} \right.\)
Lời giải:
a) \(\overrightarrow m = (2a + 3;b - 1)\) và \(\overrightarrow n = (1; - 2)\)
\(\overrightarrow m = \overrightarrow n \Leftrightarrow \left\{ \begin{array}{l}2a + 3 = 1\\b - 1 = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 1\\b = - 1\end{array} \right.\)
b) \(\overrightarrow u = (3a - 2;5)\)và \(\overrightarrow v = (5;2b + 1)\)
\(\overrightarrow u = \overrightarrow v \Leftrightarrow \left\{ \begin{array}{l}3a - 2 = 5\\5 = 2b + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{7}{3}\\b = 2\end{array} \right.\)
c) \(\overrightarrow x = (2a + b;2b)\) và \(\overrightarrow y = (3 + 2b;b - 3a)\)
\(\overrightarrow x = \overrightarrow y \Leftrightarrow \left\{ \begin{array}{l}2a + b = 3 + 2b\\2b = b - 3a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2a - b = 3\\3a + b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{3}{5}\\b = - \frac{9}{5}\end{array} \right.\)
Bài 9 trang 62 SBT Toán 10 - Cánh Diều
Trong mặt phẳng toạ độ Oxy, cho ba điểm không thẳng hàng A(– 4 ; 2), B(2 ; 4), C(8 ; – 2). Tìm toạ độ của điểm D sao cho tứ giác ABCD là hình bình hành.
Phương pháp:
Bước 1: Tham số hóa tọa độ điểm D và xác định tọa độ vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \)
Bước 2: Áp dụng kết quả tứ giác ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {DC} = \overrightarrow {AB} \) để tìm tọa độ điểm D
Lời giải:
Giả sử D(a; b) ta có \(\overrightarrow {DC} = (8 - a; - 2 - b)\) và \(\overrightarrow {AB} = (6;2)\)
ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {DC} = \overrightarrow {AB} \Leftrightarrow \left\{ \begin{array}{l}8 - a = 6\\ - 2 - b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = - 4\end{array} \right. \Rightarrow D(2; - 4)\)
Bài 10 trang 62 SBT Toán 10 - Cánh Diều
Trong mặt phẳng toạ độ Oxy, cho tứ giác ABCD có \(A({x_A};{y_A});B({x_B};{y_B});C({x_C};{y_C});D({x_D};{y_D})\). Chứng minh rằng tứ giác ABCD là hình bình hành khi và chỉ khi \({x_A} + {x_C} = {x_B} + {x_D}\) và \({y_A} + {y_C} = {y_B} + {y_D}\)
Lời giải:
Ta có: \(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A})\) và \(\overrightarrow {DC} = ({x_C} - {x_D};{y_C} - {y_D})\)
ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {AB} = \overrightarrow {CD} \Leftrightarrow \left\{ \begin{array}{l}{x_B} - {x_A} = {x_C} - {x_D}\\{y_B} - {y_A} = {y_C} - {y_D}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} + {x_D} = {x_C} + {x_A}\\{y_B} + {y_D} = {y_C} + {y_A}\end{array} \right.\) (ĐPCM)
Bài 11 trang 62 SBT Toán 10 - Cánh Diều
Trong mặt phẳng toạ độ Oxy, cho ba điểm không thẳng hàng M(1 ; – 2), N(3 ; 1), P(− 1 ; 2). Tìm toạ độ điểm Q sao cho tứ giác MNPQ là hình thang có MN // PQ và PQ = 2MN.
Lời giải:
Ta có: MN // PQ nên \(\overrightarrow {MN} \) và \(\overrightarrow {PQ} \) cùng phương
Mặt khác, PQ = 2MN \( \Rightarrow \overrightarrow {PQ} = 2\overrightarrow {NM} \)
Gọi tọa độ điểm Q là \(Q(a;b)\). Ta có: \(\overrightarrow {PQ} = (a + 1;b - 2)\) và \(\overrightarrow {NM} = ( - 2; - 3)\)
\( \Rightarrow \overrightarrow {PQ} = 2\overrightarrow {NM} \Leftrightarrow \left\{ \begin{array}{l}a + 1 = 2.( - 2)\\b - 2 = 2.( - 3)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a + 1 = - 4\\b - 2 = - 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 5\\b = - 4\end{array} \right.\) . Vậy Q(-5 ; -4)
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài tập cuối chương VII
- Bài 6. Ba đường conic
- Bài 5. Phương trình đường tròn
- Bài 4. Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng
- Bài 3. Phương trình đường thẳng
- Bài 2. Biểu thức tọa độ của các phép toán vectơ
- Bài 1. Tọa độ của vectơ
- Chương VII. Phương pháp tọa độ trong mặt phẳng
- Bài tập cuối chương VI
- Bài 5. Xác suất của biến cố
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!