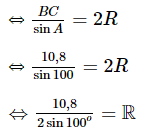Giải SBT Toán 10 trang 75 Cánh Diều tập 1
Giải bài 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 trang 75 SBT Toán 10 Cánh Diều tập 1. Bài 7. Cho tam giác ABC có (AB = 5, AC = 7, BC = 9). Tính số đo góc A và bán kính R của đường tròn ngoại tiếp tam giác ABC (làm tròn kết quả đến hàng phần mười)
Bài 1 trang 75 SBT Toán 10 - Cánh Diều
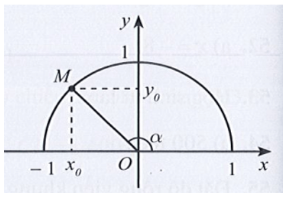
Cho 00 < \(\alpha \) < 1800. Chọn câu trả lời đúng
A. cos\(\alpha \) < 0
B. sin\(\alpha \) > 0
C. tan\(\alpha \) < 0
D. cot\(\alpha \) > 0
Phương pháp:
Dựa vào nửa đường tròn đơn vị để xét dấu các giá trị lượng giác của góc \(\alpha \)
Lời giải:
Với 0° < α < 180°, ta có:
– 1 < cosα < 1. Suy ra A sai.
0 < sinα < 1. Suy ra B đúng.
Do đó C và D sai.
Bài 2 trang 75 SBT Toán 10 - Cánh Diều
Cho 00 < \(\alpha \), \(\beta \) < 1800 và \(\alpha + \beta = {180^0}\). Chọn câu trả lời sai
A. \(\sin \alpha + \sin \beta = 0\)
B. \(\cos \alpha + \cos \beta = 0\)
C. \(\tan \alpha + \tan \beta = 0\)
D. \(\cot \alpha + \cot \beta = 0\)
Lời giải:
Đáp án đúng là A
Ta có α + β = 180° nên ta có:
sinα = sinβ ⇒ sinα + sinβ = sinα + sinα = 2sinα
Vì 0° < α, β < 180° nên sinα ≠ 0.
Do đó sinα + sinβ ≠ 0. Suy ra A sai.
cosα = – cosβ ⇒ cosα + cosβ = 0. Suy ra B đúng.
tanα = – tanβ ⇒ tanα + tanβ = 0. Suy ra C đúng.
cotα = – cotβ ⇒ cotα + cotβ = 0. Suy ra D đúng.
Bài 3 trang 75 SBT Toán 10 - Cánh Diều
Tính giá trị của biểu thức \(T = {\sin ^2}{25^0} + {\sin ^2}{75^0} + {\sin ^2}{115^0} + {\sin ^2}{165^0}\)
Phương pháp:
Bước 1: Xét mối liên hệ giữa các góc trong T với nhau hoặc với các góc trung gian
Bước 2: Biến đổi các giá trị lượng giác của các góc về chung giá trị lượng giác của một góc
Bước 3: Sử dụng công thức lượng giác \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) để rút gọn biểu thức T
Lời giải:
T = sin225° + sin275° + sin2115° + sin2165°
= sin225° + sin275° + sin275° + sin225°
= 2sin225° + 2sin275°
= 2sin225° + 2cos225°
= 2(sin225° + cos225°)
= 2.1 = 2.
Bài 4 trang 75 SBT Toán 10 - Cánh Diều
Cho \(\tan \alpha = - 2\). Tính giá trị biểu thức \(P = \frac{{\cos \alpha + 3\sin \alpha }}{{\sin \alpha + 3\cos \alpha }}\)
Phương pháp:
Bước 1: Chia cả tử và mẫu của biểu thức P cho \(\cos \alpha \)
Bước 2: Biến đổi biểu thức P sao cho xuất hiện duy nhất giá trị \(\tan \alpha \)
Bước 3: Thay \(\tan \alpha = - 2\) rồi tính giá trị biểu thức P
Lời giải:
Do \(\tan \alpha = - 2\) nên \(\cos \alpha \ne 0\). Chia cả tử và mẫu của biểu thức P cho \(\cos \alpha \) ta có:
\(P = \frac{{\frac{{\cos \alpha + 3\sin \alpha }}{{\cos \alpha }}}}{{\frac{{\sin \alpha + 3\cos \alpha }}{{\cos \alpha }}}} = \frac{{1 + 3\frac{{\sin \alpha }}{{\cos \alpha }}}}{{\frac{{\sin \alpha }}{{\cos \alpha }} + 3}} = \frac{{1 + 3\tan \alpha }}{{\tan \alpha + 3}} = \frac{{1 + 3.( - 2)}}{{ - 2 + 3}} = - 5\)
Vậy với \(\tan \alpha = - 2\) thì P = -5
Bài 5 trang 75 SBT Toán 10 - Cánh Diều
Cho tam giác ABC có \(AB = 6,AC = 8,\widehat A = {100^0}\). Tính độ dài cạnh BC và bán kính R của đường tròn ngoại tiếp tam giác (làm tròn kết quả đến hàng phần mười)
Phương pháp:
Bước 1: Sử dụng định lí cosin để tính độ dài BC
Bước 2: Sử dụng định lí sin để tính bán kính R
Lời giải:
Xét tam giác ABC, có:
BC2 = AB2 + AC2 – 2.AB.AC.cosA (định lí cos)
⇔ BC2 = 62 + 82 – 2.6.8.cos100°
⇔ BC2 ≈ 116,7
⇔ BC ≈ 10,8.
Áp dụng định lí sin trong tam giác ABC, ta có:
⇔ R ≈ 5,5.
Vậy BC ≈ 10,8 và R ≈ 5,5.
Bài 6 trang 75 SBT Toán 10 - Cánh Diều
Cho tam giác ABC có \(\widehat B = {60^0},\widehat C = {105^0}\) và \(BC = 15\). Tính độ dài cạnh AC và bán kính R của đường tròn ngoại tiếp tam giác ABC (làm tròn kết quả đến hàng phần mười)
Lời giải:
Ta có: \(\widehat A = {180^0} - (\widehat B + \widehat C) = {15^0}\)
Áp dụng định lí sin cho ∆ABC ta có: \(\left\{ \begin{array}{l}\frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin {\rm{A}}}} \Rightarrow AC = \frac{{BC.\sin B}}{{\sin {\rm{A}}}} = \frac{{15.\sin {{60}^0}}}{{\sin {{15}^0}}} \approx 50,2\\\frac{{BC}}{{\sin {\rm{A}}}} = 2R \Rightarrow R = \frac{{BC}}{{2\sin {\rm{A}}}} = \frac{{15}}{{2\sin {{15}^0}}} \approx 29\end{array} \right.\)
Bài 7 trang 75 SBT Toán 10 - Cánh Diều
Cho tam giác ABC có \(AB = 5,AC = 7,BC = 9\). Tính số đo góc A và bán kính R của đường tròn ngoại tiếp tam giác ABC (làm tròn kết quả đến hàng phần mười)
Lời giải:
Áp dụng định lí cosin cho ∆ABC ta có: \(B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\)
\( \Rightarrow \cos A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}} = \frac{{{5^2} + {7^2} - {9^2}}}{{2.5.7}} = - \frac{1}{{10}}\) \( \Rightarrow \widehat A \approx {96^0}\)
Áp dụng định lí sin cho ∆ABC ta có: \(\frac{{BC}}{{\sin {\rm{A}}}} = 2R \Rightarrow R = \frac{{BC}}{{2\sin {\rm{A}}}} = \frac{9}{{2.\sin {{96}^0}}} \approx 4,5\)
Bài 8 trang 75 SBT Toán 10 - Cánh Diều
Cho hình bình hành ABCD có \(AB = a,BC = b,AC = m,BD = n\). Chứng minh \({m^2} + {n^2} = 2({a^2} + {b^2})\)
Phương pháp:
Bước 1: Sử dụng định lí cosin cho hai tam giác ∆ABC và ∆ADB để tính độ dài AC và BD
Bước 2: Xét mối liên hệ của các góc trong hình bình hành
Bước 3: Biến đổi các đẳng thức. Kết luận
Lời gải:
Xét tam giác ABC, có:
AC2 = AB2 + BC2 – 2.AB.BC.cosB (định lí cos)
⇔ m2 = a2 + b2 – 2.a.b.cosB (1)
Vì ABCD là hình bình hành nên AD = BC = b,
Vì ⇒ cosA = – cosB ⇒ cosA + cosB = 0
Xét tam giác ABD, có:
BD2 = AB2 + AD2 – 2.AB.AD.cosA (định lí cos)
⇔ n2 = a2 + b2 – 2.a.b.cosA (2)
Cộng vế với vế của (1) và (2), ta được:
m2 + n2 = a2 + b2 – 2.a.b.cosB + a2 + b2 – 2.a.b.cosB
⇔ m2 + n2 = 2(a2 + b2) – 2.a.b.(cosB + cosA)
⇔ m2 + n2 = 2(a2 + b2) – 2.a.b.0
⇔ m2 + n2 = 2(a2 + b2).
Bài 9 trang 75 SBT Toán 10 - Cánh Diều
Từ một tấm tôn hình tròn bán kính R = 1 m, bạn trí muốn cắt ra một hình tam giác ABC có các góc A = 450, B = 750. Hỏi bạn Trí phải cắt miếng tôn theo hai dây cung AB, BC có độ dài lần lượt bằng bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?
Phương pháp:
Tính góc C và sử dụng định lí sin để tính độ dài cạnh AB, BC của ∆ABC rồi kết luận
Lời giải:
Ta có: \(\widehat C = {180^0} - (\widehat A + \widehat B) = {60^0}\)
Áp dụng định lí sin cho ∆ABC ta có: \(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin {\rm{A}}}} = 2R = 2 \Rightarrow \left\{ \begin{array}{l}AB = 2\sin C = 2\sin {60^0} \approx 1,73\\BC = 2\sin {\rm{A}} = 2\sin {45^0} \approx 1,41\end{array} \right.\)
Vậy bạn Trí cần cắt miếng tôn theo hai dây cung AB, AC có độ dài lần lượt là 1,73 m và 1, 41 m
Bài 10 trang 75 SBT Toán 10 - Cánh Diều
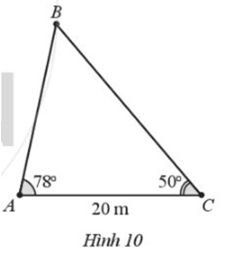
Một cây cao bị nghiêng so với mặt đất góc 780. Từ vị trí C cách gốc cây 20 m, người ta tiến hành đo đạc và thu được kết quả \(\widehat {ACB} = {50^0}\) với B là vị trí ngọn cây (Hình 10). Tính khoảng cách từ gốc cây (điểm A) đến ngọn cây (điểm B) (làm tròn kết quả đến hàng phần mười theo đơn vị mét)
Lời giải:
Ta có: \(\widehat B = {180^0} - (\widehat A + \widehat C) = {52^0}\)
Áp dụng định lí sin cho ∆ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} \Rightarrow AB = \frac{{AC.\sin C}}{{\sin B}} = \frac{{20.\sin {{50}^0}}}{{\sin {{52}^0}}} \approx 19,4\)
Vậy khoảng cách từ gốc cây đến ngọn cây là 19,4 m
Bài 11 trang 75 SBT Toán 10 - Cánh Diều
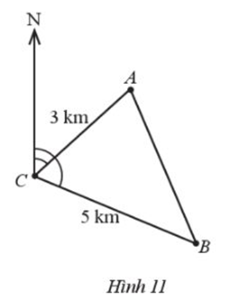
Tàu A cách cảng C một khoảng 3 km và lệch hướng bắc một góc 47,450. Tàu B cách cảng C một khoảng 5 km và lệch hướng bắc một góc 112,900 (Hình 11). Hỏi khoảng cách giữa hai tàu là bao nhiêu kilomet (làm tròn kết quả đến hàng phần trăm)?
Phương pháp:
Bước 1: Từ giả thiết xác định số đo các góc \(\widehat {NCA},\widehat {NCB},\widehat {ACB}\)
Bước 2: Áp dụng định lí cosin cho ∆ABC để tính độ dài AB rồi kết luận
Lời giải:
Theo giả thiết,
\(\widehat {NCA} = 47,{45^0},\widehat {NCB} = 112,{90^0} \Rightarrow \widehat {ACB} = \widehat {NCB} - \widehat {NCA} = 65,{45^0}\)
Áp dụng định lí cosin cho ∆ABC ta có:
\(A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos \widehat {ACB}\)
\( \Rightarrow AB = \sqrt {A{C^2} + B{C^2} - 2.AC.BC.\cos \widehat {ACB}} \)
\( = \sqrt {{3^2} + {5^2} - 2.3.5.\cos 65,{{45}^0}} \approx 4,64\)
Vậy khoảng cách giữa hai tàu là 4,64 km
Sachbaitap.com
Bài viết liên quan
Các bài khác cùng chuyên mục
- Bài tập cuối chương VII
- Bài 6. Ba đường conic
- Bài 5. Phương trình đường tròn
- Bài 4. Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng
- Bài 3. Phương trình đường thẳng
- Bài 2. Biểu thức tọa độ của các phép toán vectơ
- Bài 1. Tọa độ của vectơ
- Chương VII. Phương pháp tọa độ trong mặt phẳng
- Bài tập cuối chương VI
- Bài 5. Xác suất của biến cố
- Bài 22 Đọc mở rộng trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Luyện viết đoạn văn thể hiện tình cảm, cảm xúc về một sự việc trang 111 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 22 Bộ đội về làng trang 109 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 2) trang 108 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Luyện tập về câu ghép trang 107 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 21 Anh hùng lao động Trần Đại Nghĩa trang 106 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đền ơn đáp nghĩa trang 104 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Đánh giá, chỉnh sửa đoạn văn nêu ý kiến tán thành một sự vật, hiện tượng trang 103 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 20 Cụ Đồ Chiểu trang 101 SGK Tiếng Việt 5 Kết nối tri thức tập 2
- Bài 19 Viết đoạn văn nêu ý kiến tán thành một sự việc, hiện tượng (Bài viết số 1) trang 100 SGK Tiếng Việt 5 Kết nối tri thức tập 2
 Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!
Tải app loigiaihay.com cho Android để lưu và xem mà không cần mạng!