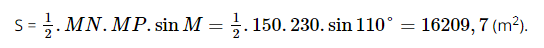Giải SBT Toán 10 trang 79, 80, 81 Cánh Diều tập 1

Bài 12 trang 79 SBT Toán 10 - Cánh Diều

Cho tam giác ABC có \(AB = 6,5cm,AC = 8,5cm,\widehat A = {125^0}\). Tính (làm tròn kết quả đến hàng phần mười theo đơn vị tương ứng):

a) Độ dài cạnh BC

b) Số đo các góc B, C

c) Diện tích tam giác ABC 

Lời giải:

a) Áp dụng định lí cosin cho ∆ABC ta có: \(B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\)

\( \Rightarrow BC = \sqrt {A{B^2} + A{C^2} - 2.AB.AC.\cos A} \)

\( = \sqrt {6,{5^2} + 8,{5^2} - 2.6,5.8,5.\cos {{125}^0}}  \approx 13,3\)(cm)

b) Áp dụng định lí sin cho ∆ABC ta có:

 \(\frac{{BC}}{{\sin {\rm{A}}}} = \frac{{AB}}{{\sin C}} \Rightarrow \sin C = \frac{{AB.\sin A}}{{BC}} \Rightarrow \widehat C \approx 23,{6^0}\)

Ta có: \(\widehat B = {180^0} - (\widehat A + \widehat C) = 31,{4^0}\)

c) \({S_{ABC}} = \frac{1}{2}AB.AC\sin A = \frac{1}{2}.6,5.8,5.\sin {125^0} \approx 22,6\) (cm²)

Bài 13 trang 79 SBT Toán 10 - Cánh Diều

Cho tam giác ABC có \(BC = 50\)cm, \(\widehat B = {65^0},\widehat C = {45^0}\). Tính (làm tròn kết quả đến hàng phần mười theo đơn vị xentimet)

a) Độ dài cạnh AB, AC

b) Bán kính đường tròn ngoại tiếp tam giác ABC

Lời giải:

Ta có: \(\widehat A = {180^0} - (\widehat B + \widehat C) = {70^0}\)

a) Áp dụng định lí sin cho ∆ABC ta có:

\(\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} \Rightarrow \left\{ \begin{array}{l}AB = \frac{{BC.\sin C}}{{\sin A}} = \frac{{50.\sin {{45}^0}}}{{\sin {{70}^0}}} \approx 37,6cm\\AC = \frac{{BC.\sin B}}{{\sin A}} = \frac{{50.\sin {{65}^0}}}{{\sin {{70}^0}}} \approx 48,2cm\end{array} \right.\)

b) Áp dụng định lí sin cho ∆ABC ta có:

 \(\frac{{BC}}{{\sin {\rm{A}}}} = 2R \Rightarrow R = \frac{{BC}}{{2\sin A}} = \frac{{50}}{{2.\sin {{70}^0}}} \approx 26,6cm\)

Bài 14 trang 79 SBT Toán 10 - Cánh Diều

Cho tam giác ABC có \(AB = 5,AC = 8,BC = 9\). Tính (làm tròn kết quả đến hàng phần mười)

a) Số đo các góc A, B, C

b) Diện tích tam giác ABC 

Lời giải:

a) Áp dụng định lí cosin cho ∆ABC ta có:

 \(\left\{ \begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\\A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\end{array} \right.\)

\( \Rightarrow \left\{ \begin{array}{l}\cos A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}} = \frac{{{5^2} + {8^2} - {9^2}}}{{2.5.8}} = \frac{1}{{10}}\\\cos B = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}} = \frac{{{5^2} + {9^2} - {8^2}}}{{2.5.9}} = \frac{7}{{15}}\end{array} \right.\)

\( \Rightarrow \left\{ \begin{array}{l}\widehat A \approx 84,{3^0}\\\widehat B \approx 62,{2^0}\end{array} \right.\)

Ta có: \(\widehat C = {180^0} - (\widehat A + \widehat B) = 33,{5^0}\)

b) \({S_{ABC}} = \frac{1}{2}AB.AC\sin A = \frac{1}{2}.5.8.\sin 84,{3^0} \approx 19,9\)

Bài 15 trang 79 SBT Toán 10 - Cánh Diều

Cho tam giác ABC có \(\widehat B = {60^0},BC = 8,AB + AC = 12\). Tính độ dài các cạnh AB, AC           

Lời giải:

Đặt AB = x (x > 0)

Ta có AB + AC = 12 ⇒ AC = 12 – AB = 12 – x

Xét tam giác ABC, ta có:

AC² = AB² + BC² – 2.AB.BC.cosB

⇔ (12 – x)² = x² + 8² – 2.x.8.cos60°

⇔ 144 – 24x + x² = x² + 64 – 8x

⇔ – 16x = – 80

⇔ x = 5

⇒ 12 – x = 12 – 5 = 7

Vậy AB = 5cm, AC = 7cm.

Bài 16 trang 79 SBT Toán 10 - Cánh Diều

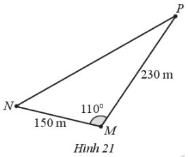
Gia đình bạn An sở hữu một mảnh đất hình tam giác. Chiều dài của hàng rào MN là 150 m, chiều dài của hàng rào MP là 230 m. Góc giữa hai hàng rào MN và MP là 110⁰ (Hình 21)

a) Diện tích mảnh đất mà gia đình bạn An sở hữu là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)?

b) Chiều dài hàng rào NP là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

Lời giải:

a) Diện tích mảnh đất gia đình An bằng diện tích hình tam giác MNP và bằng:

Vậy diện tích mảnh đất gia đình An là 16 209,7 m².

b) Xét tam giác MNP, có:

NP² = MN² + MP² – 2.MN.MP.cosM

⇔ NP² = 150² + 230² – 2.150.230.cos110°

⇔ NP² = 150² + 230² – 2.150.230.cos110°

⇔ NP² ≈ 98 999,4

⇔ NP ≈ 314,6

Vậy hàng rào NP dài 314,6 mét.

Bài 17 trang 80 SBT Toán 10 - Cánh Diều

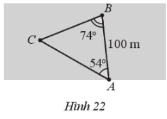
Hai người A và B cùng quan sát một con tàu đang neo đậu ngoài khơi tại vị trí C. Người A đứng trên bờ biển, người B đứng trên một hòn đảo cách bờ một khoảng AB= 100 m. Hai người tiến hành đo đạc và thu được kết quả: \(\widehat {CAB} = {54^0},\widehat {CBA} = {74^0}\) (Hình 22). Hỏi con tàu cách hòn đảo bao xa (làm tròn kết quả đến hàng phần mười theo đơn vị mét)?

Lời giải:

Ta có:  \(\widehat {ACB} = {180^0} - (\widehat {CBA} + \widehat {CAB}) = {52^0}\)

Áp dụng định lí sin cho ∆ABC ta có: \(\frac{{BC}}{{\sin \widehat {CAB}}} = \frac{{AB}}{{\sin \widehat {ACB}}} \Rightarrow BC = \frac{{AB.\sin \widehat {CAB}}}{{\sin \widehat {ACB}}} = \frac{{100.\sin {{54}^0}}}{{\sin {{52}^0}}} \approx 102,7\)

Vậy con tàu cách hòn đảo 102,7 m

 Bài 18 trang 80 SBT Toán 10 - Cánh Diều

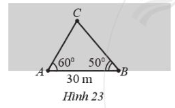
Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một con tàu C đang neo đậu ngoài khơi. Người đó tiến hành đo đạc và thu được kết quả: \(AB = 30m,\widehat {CAB} = {60^0},\widehat {CBA} = {50^0}\) (Hình 23). Tính khoảng cách từ vị trí A đến con tàu C(làm tròn kết quả đến hàng phần mười theo đơn vị mét)?

Lời giải:

Ta có:  \(\widehat {ACB} = {180^0} - (\widehat {CBA} + \widehat {CAB}) = {70^0}\)

Áp dụng định lí sin cho ∆ABC ta có: \(\frac{{AC}}{{\sin \widehat {CBA}}} = \frac{{AB}}{{\sin \widehat {ACB}}} \Rightarrow AC = \frac{{AB.\sin \widehat {CBA}}}{{\sin \widehat {ACB}}} = \frac{{30.\sin {{50}^0}}}{{\sin {{70}^0}}} \approx 24,5\)

Vậy khoảng cách từ vị trí A đến con tàu C  là 24,5 m

Bài 19 trang 80 SBT Toán 10 - Cánh Diều

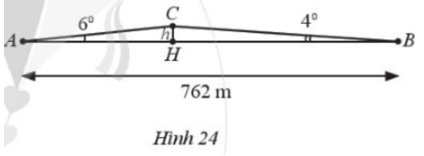
Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B) phải leo lên và xuống một con dốc (Hình 24). Cho biết đoạn thẳng AB dài 762 m, \(\widehat A = {6^0},\widehat B = {4^0}\)

a) Tính chiều cao h của con dốc theo đơn vị mét (làm tròn kết quả đến hàng đơn vị)

b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ trung bình lên dốc là 4 km/h và tốc độ trung bình khi xuống dốc là 19 km/h.

Lời giải:

a) Ta có: \(\widehat {ACB} = {180^0} - (\widehat {CBA} + \widehat {CAB}) = {170^0}\)

Áp dụng định lí sin cho ∆ABC ta có: \(\frac{{AC}}{{\sin \widehat {CBA}}} = \frac{{AB}}{{\sin \widehat {ACB}}} \Rightarrow AC = \frac{{AB.\sin \widehat {CBA}}}{{\sin \widehat {ACB}}} = \frac{{762.\sin {4^0}}}{{\sin {{170}^0}}} \approx 306\) (m)

Xét ∆AHC vuông tại H, AC = 306 m, \(\widehat {CAH} = {6^0}\) có: \(CH = AC.\sin \widehat {CAH} = 306.\sin {6^0} \approx 32\) 

Vậy chiều cao h của con dốc là 32 m

b) Áp dụng định lí sin cho ∆ABC ta có: \(\frac{{BC}}{{\sin \widehat {BAC}}} = \frac{{AB}}{{\sin \widehat {ACB}}} \Rightarrow BC = \frac{{AB.\sin \widehat {BAC}}}{{\sin \widehat {ACB}}} = \frac{{762.\sin {6^0}}}{{\sin {{170}^0}}} \approx 459\) (m)

Ta có: \(AC \approx 0,306\) km, \(BC \approx 0,459\) km

Thời gian bạn An đi quãng đường AC là \({t_1} = \frac{{0,306}}{4}\) (giờ)

Thời gian bạn An đi quãng đường AC là \({t_2} = \frac{{0,459}}{{19}}\) (giờ)

\( \Rightarrow \)Bạn An đi từ nhà đến trường hết \(t = {t_1} + {t_2} = \frac{{0,036}}{4} + \frac{{0,459}}{{19}} \approx 0,1\) giờ = 6 phút

Vậy bạn An đến trường lúc 6 giờ 6 phút.

Bài 20 trang 80 SBT Toán 10 - Cánh Diều

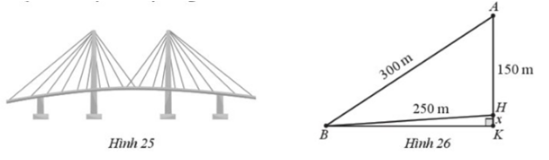
Quan sát cây cầu dây văng minh họa ở Hình 25

Tại trụ cao nhất, khoảng cách từ đỉnh trụ (vị trí A) tới chân trụ trên mặt cầu (vị trí H) là 150 m, độ dài dây văng dài nhất nối từ đỉnh trụ xuống mặt cầu (vị trí B) là 300 m, khoảng cách từ chân dây văng dài nhất tới chân trụ trên mặt cầu là 250 m (Hình 26). Tính độ dốc của cầu qua trụ nói trên (làm tròn kết quả đến hàng phần mười theo đơn vị độ).

Lời giải:

Áp dụng định lí cosin cho ∆ABH ta có: \(A{B^2} = B{H^2} + A{H^2} - 2.BH.AH.\cos \widehat {AHB}\)

\( \Rightarrow \cos \widehat {AHB} = \frac{{B{H^2} + A{H^2} - A{B^2}}}{{2.BH.AH}} = \frac{{{{250}^2} + {{150}^2} - {{300}^2}}}{{2.250.150}} =  - \frac{1}{{15}}\)\( \Rightarrow \widehat {AHB} \approx 93,{8^0}\)

Xét ∆HBK có \(\widehat {AHB}\) là góc ngoài của tam giác HBK

\( \Rightarrow \widehat {AHB} = \widehat {HBK} + \widehat {HKB} \Rightarrow \widehat {HBK} = \widehat {AHB} - \widehat {HKB} = 93,{8^0} - {90^0} = 3,{8^0}\)

Vậy độ dốc của cầu qua trụ là 3,8⁰

Bài 21 trang 81 SBT Toán 10 - Cánh Diều

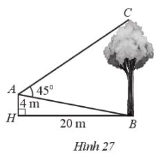
Một người đứng ở vị trí Atrên nóc một ngôi nhà cao 4 m đang quan sát đang quan sát một cây cao cách ngôi nhà 20 m và đo được \(\widehat {BAC} = {45^0}\) (Hình 27). Tính chiều cao của cây đó (làm tròn kết quả đến hàng phần mười theo đơn vị mét)

Lời giải:

Áp dụng định lí Pytago cho ∆ABH vuông tại H ta có: \(AB = \sqrt {A{H^2} + H{B^2}}  = \sqrt {{4^2} + {{20}^2}}  \approx 20,4\) (m)

Xét ∆ABH vuông tại H  có \(\tan \widehat {ABH} = \frac{{AH}}{{BH}} = \frac{1}{5} \Rightarrow \widehat {ABH} \approx 11,{3^0}\)

Ta có: \(\widehat {ABH} + \widehat {ABC} = {90^0} \Rightarrow \widehat {ABC} = {90^0} - \widehat {ABH} = 78,{7^0}\) \( \Rightarrow \widehat {ACB} = {180^0} - (\widehat {ABC} + \widehat {CAB}) = 56,{3^0}\)

Áp dụng định lí sin cho ∆ABC ta có: \(\frac{{BC}}{{\sin \widehat {BAC}}} = \frac{{AB}}{{\sin \widehat {ACB}}} \Rightarrow BC = \frac{{AB.\sin \widehat {BAC}}}{{\sin \widehat {ACB}}} = \frac{{20,4.\sin {{45}^0}}}{{\sin 56,{3^0}}} \approx 17,3\) (m)

Vậy chiều cao của cây là 17,3 m

 Sachbaitap.com