Câu 43 trang 45 Sách Bài Tập (SBT) Toán lớp 7 tập 2

Cho hai đường thẳng AB và CD cắt nhau tại O. Tìm tập hợp các điểm cách đều hai đường thẳng AB và CD.

Giải

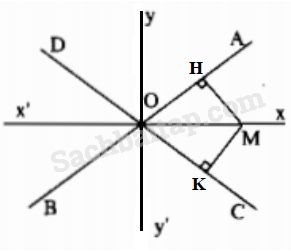
Xét \(M\) nằm trong góc AOC và cách đều OA và OC.

Kẻ \(MH \bot OA,MK \bot {\rm{O}}C\) nên MH = MK

Xét hai tam giác vuông MHO và MKO:

               \(\widehat {MHO} = \widehat {MK{\rm{O}}} = 90^\circ \)

               MH = MK

               OM cạnh huyền chung  

Do đó ∆MHO = ∆MKO (cạnh huyền - cạnh góc vuông)

\( \Rightarrow \widehat {MOH} = \widehat {MOK}\) (2 góc tương ứng)

=>OM là tia phân giác của \(\widehat {AOC}\)

Ngược lại, M nằm trên tia phân giác của \(\widehat {AOC}\)

Xét hai tam giác vuông MHO và MKO:

                 \(\widehat {MHO} = \widehat {MK{\rm{O}}} = 90^\circ \)

                 \(\widehat {MOH} = \widehat {MOK}\)

                 OM cạnh huyền chung  

Do đó ∆MHO = ∆MKO (cạnh huyền – góc nhọn)

\( \Rightarrow \) MH = MK (2 cạnh tương ứng)

Vậy tập hợp các điểm M cách đều OA và OC là tia phân giác Ox của góc AOC.

Tương tự M nằm trong các góc AOD, DOB, BOC tập hợp các điểm M là tia phân giác Oy, Ox’, Oy’.

Vậy tập hợp các điểm M cách đều hai đường thẳng AB và CD cắt nhau tại O là hai đường thẳng xx’ và yy’ là đường phân giác của các góc tạo bởi hai đường thẳng AB và CD.

Sachbaitap.com