Câu 6.41 trang 203 SBT Đại số 10 Nâng cao

Chứng minh công thức \(\cos 2\alpha  = 2{\cos ^2}\alpha  - 1\)(với \(0 < \alpha  < \dfrac{\pi }{4}\)) bằng “phương pháp hình học” như sau:

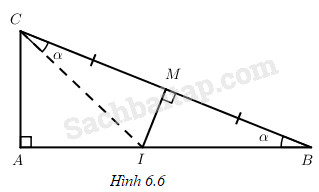
Xét tam giác vuông ABC với \(\widehat A = \dfrac{\pi }{2},\widehat B = \alpha .\) Kẻ đường trung trực của đoạn BC cắt AB tại I. Dễ thấy: \(\cos 2\alpha  = \dfrac{{AI}}{{IC}};\cos \alpha  = \dfrac{{AB}}{{BC}}\) (h. 6.6); từ đó hãy suy ra

\(\cos 2\alpha  = 2{\cos ^2}\alpha  - 1\).

Giải:

Dễ thấy \(BI = IC,\)

nên

\(\begin{array}{l}\cos 2\alpha  = \dfrac{{AI}}{{IC}} = \dfrac{{AI}}{{BI}} = \dfrac{{AB - BI}}{{BI}}\\ = \dfrac{{AB}}{{BI}} - 1 = \dfrac{{AB}}{{BC}}.\dfrac{{2BM}}{{BI}} - 1\end{array}\)

Mà

\(\cos \alpha  = \dfrac{{AB}}{{BC}} = \dfrac{{BM}}{{BI}}\), nên \(\cos 2\alpha  = 2{\cos ^2}\alpha  - 1\).

Sachbaitap.com