Chứng minh rằng giao điểm hai đường chéo của hình thang cân nằm trên trục đối xứng của hình thang cân.

Xem thêm: Bài 6. Đối xứng trục

Chứng minh rằng giao điểm hai đường chéo của hình thang cân nằm trên trục đối xứng của hình thang cân.

Giải:

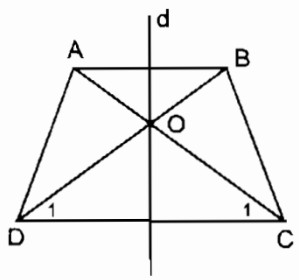
Hình thang cân ABCD có AB // CD. Gọi O là giao điểm của hai đường chéo AC và BD.

Xét ∆ ADC và ∆ BCD:

AD = BC ( tính chất hình thang cân)

AC = BD ( tính chất hình thang cân)

CD cạnh chung

Do đó ∆ ADC = ∆ BCD (c.c.c)

\( \Rightarrow {\widehat D_1} = {\widehat C_1}\)

⇒ ∆ OCD cân tại O

⇒ OC = OD nên O nằm trên đường trung trực của CD.

Trục đối xứng của hình thang cân là đường thẳng trung trực của hai đáy.

Vậy O thuộc trục đối xứng của hình thang cân.

Sachbaitap.com

Bài tiếp theo

Xem lời giải SGK - Toán 8 - Xem ngay

Báo lỗi - Góp ý

>> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.