Giải bài 1, 2, 3, 4, 5 trang 31 SGK Toán 6 tập 2 Chân trời sáng tạo

Bài 1 trang 31 SGK Toán 6 tập 2 - Chân trời sáng tạo

Viết các phân số sau đây dưới dạng số thập phân

\(\frac{{ - 3519}}{{100}};\,\frac{{ - 778}}{{10}};\,\,\frac{{ - 23}}{{1000}};\,\frac{{88}}{{100}}\).

Phương pháp:

- Các phân số thập phân dương được viết dưới dạng số thập phân dương.

- Các phân số thập phân âm được viết dưới dạng số thập phân âm.

Lời giải:

a) Các phân số trên đều là phân số thập phân.

Cách đổi các phân số thập phân sang số thập phân thì ta quy về bài toán chia một số cho 10; 100; 1 000 (kết quả để dưới dạng số thập phân).

Quy tắc: Muốn chia một số cho 10; 100; 1 000 ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba, … chữ số.

Đổi lần lượt các phân số thập phân trên ra số thập phân, ta được:

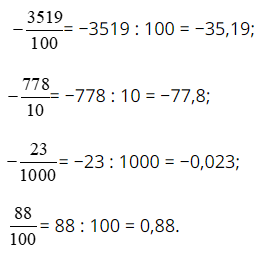
Bài 2 trang 31 SGK Toán 6 tập 2 - Chân trời sáng tạo

Viết các số thập phân sau đây dưới dạng phân số thập phân

- 312,5;  0,205;  - 10,09;  - 1,110.

Phương pháp:

Phân số thập phân là phân số có mẫu số là luỹ thừa của 10.

Lời giải:

- Các phân số thập phân được viết dưới dạng số thập phân.

- Số các chữ số thập phân bằng đúng số các chữ số 0 ở mẫu của phân số thập phân.

Đổi lần lượt các số thập phân trên ra phân số thập phân, ta được:

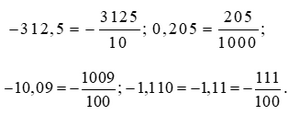
Bài 3 trang 31 SGK Toán 6 tập 2 - Chân trời sáng tạo

Tìm số đối của các số thập phân sau:

9,32;  -12,34;  -0,7;  3,333

Phương pháp:

Số đối của số a là – a.

Lời giải:

Cách tìm số đối của một số thập phân: ta thêm dấu trừ vào trước số thập phân đó.

Số đối của 9,32 là −9,32;

Số đối của −12,34 là −(−12,34) hay 12,34;

Số đối của −0,7 là −(−0,7) = 0,7;

Số đối của 3,333 là −3,333.

Bài 4 trang 31 SGK Toán 6 tập 2 - Chân trời sáng tạo

Hãy sắp xếp các số thập phân sau theo thứ tự tăng dần:

- 2,99; - 2,9; 0,7; 1; 22,1.

Phương pháp:

So sánh các số rồi sắp xếp các số thập phân sau theo thứ tự tăng dần.

Lời giải:

Để sắp xếp các số thập phân sau theo thứ tự tăng dần, ta làm như sau:

Bước 1: Chia thành 2 nhóm số thập dương và số thập phân âm, vì số thập phân âm luôn nhỏ hơn số thập phân dương.

Bước 2: Ta so sánh các số thập phân theo nhóm với nhau:

- Nhóm các số thập phân dương: ta so sánh phần nguyên với nhau, số nào có phần nguyên lớn hơn thì lớn hơn. Nếu phần nguyên bằng nhau thì ta lần lượt so sánh các hàng ở phần thập phân.

- Nhóm các số thập phân âm: ta so sánh số đối của chúng, số nào có số đối lớn hơn thì nhỏ hơn.

* Phân loại:

- Nhóm các số thập phân dương: 0,7; 1; 22,1.

- Nhóm các số thập phân âm: −2,99; −2,9.

* So sánh các số thập phân trong theo nhóm: 

- Nhóm các số thập phân dương: ta so sánh phần nguyên của các số trên, vì 0 < 1 < 22 nên 0,7 < 1 < 22,1.

- Nhóm các số thập phân âm: 

+ Số đối của các số −2,99; −2,9 lần lượt là 2,99; 2,9.

+ So sánh phần nguyên: cả hai số 2,99 và 2,9 đều có phần nguyên là 2. 

+ So sánh phần thập phân: Hàng phần mười của hai số đều là 9. 

Ta tiếp tục so sánh hàng phần trăm: chữ số hàng phần trăm của 2,99 và 2,9 lần lượt là 9 và 0. Vì 9 > 0 nên 2,99 > 2,9.

Do đó −2,99 < −2,9.

Từ đó ta suy ra −2,99 < −2,9 < 0,7 < 1 < 22,1.

Vậy các số được sắp xếp thứ tự tăng dần là: −2,99; −2,9; 0,7; 1; 22,1.

Bài 5 trang 31 SGK Toán 6 tập 2 - Chân trời sáng tạo

Hãy sắp xếp các số sau theo thứ tự giảm dần

0,6;  \(\frac{{ - 5}}{6}\); \(\frac{{ - 4}}{3}\); 0; \(\frac{8}{{13}}\); -1,75.

Phương pháp:

So sánh các số âm và các số dương rồi sắp xếp các số thập phân sau theo thứ tự giảm dần.

Lời giải:

Sachbaitap.com